
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П Л А Н. 1. Конспект, підготовка до практичного заняття. 1. Конспект, підготовка до практичного заняття
|
|
|
|
Завдання додому
1. Конспект, підготовка до практичного заняття
[1] с. 191-222
[2] с. 176-194
2. Самостійна робота №8 “Задача про неперервне нарахування відсотків”
(2 год.) [2] с. 159-161
3. Самостійна робота №9 “Поняття про еластичність функції”
(2 год.) [2] с. 196-198
Питання для самоконтролю
1. Неперервність функції у=f (x).
2. Похідна функції. Геометричний та економічний зміст.
3. Основні правила диференціювання.
4. Таблиця похідних.
5. Похідна складної функції.
6. Означення диференціала та його зміст.
7. Інваріантність форми диференціала.
8. Застосування диференціала в наближених обчисленнях.
Л Е К Ц І Я 15
Тема: Дослідження функцій. Побудова графіків.
Мета: сформувати поняття екстремума функції, опуклості і вгнутості кривих, асимптоти кривої, ознайомити з схемою дослідження функції та побудовою графіка.
Література: [1, с. 246-266]; [6, с.249-254].
1. Екстремум функції.
2. Опуклість і вгнутість кривих.
3. Асимптоти кривої.
4. Схема дослідження функції та побудова графіка.
5 Видача індивідуального завдання.
1. Границя відношення двох функцій (у випадках невизначеності виду 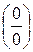 і
і 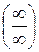 при
при 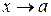 або
або 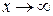 ) дорівнює границі відношення похідних цих функцій.
) дорівнює границі відношення похідних цих функцій.
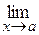
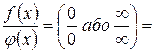
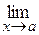
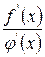
(або 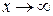 ) (або
) (або 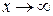 )
)
Правило Лопіталя використовується з застосуванням особливих границь і властивостей границь.
Приклад: 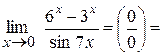
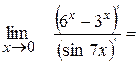
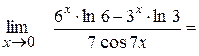
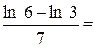
=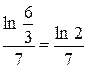
2. Розглянемо функцію у= f (x), 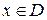 .
.
 1) Функція називається зростаючою, якщо при х2 > х1 f (x2) > f (x1).
1) Функція називається зростаючою, якщо при х2 > х1 f (x2) > f (x1).


 y
y
f (x1) f (x2)


 0 x1 x2 x
0 x1 x2 x
2) Функція називається спадною, якщо при x1 > x2 f (x2) < f (x1).
y
 | |||
 | |||
 f (x1)
f (x1)


 f (x2)
f (x2)
0 x1 x2 x
Функція, яка або тільки зростає, або тільки спадає на деякому інтервалі, називається монотонною на цьому інтервалі.
Достатні умови монотонності функції.
1. Якщо в кожній точці інтервалу 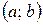 функція має додатню похідну, то в цьому інтервалі функція зростає, тобто нерівність
функція має додатню похідну, то в цьому інтервалі функція зростає, тобто нерівність 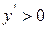 є достатньою умовою зростання функції.
є достатньою умовою зростання функції.
2. Якщо 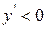 , то в інтервалі
, то в інтервалі 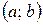 функція спадає.
функція спадає.
3. Якщо 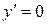 в кожній точці інтервалу
в кожній точці інтервалу 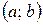 , то в цьому інтервалі функція постійна.
, то в цьому інтервалі функція постійна.
 у
у
у=с
 с
с
 0 х
0 х
 |

 y
y
у=f (x) 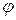 - гострий кут
- гострий кут

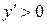
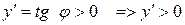
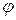
 0 x
0 x
3. Розглянемо функцію у= f (x), х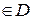 .
.
х0 – точка max, якщо значення функції в цій точці є найбільшим в порівнянні із значенням функції в деякому околі точки х0.
 у
у

 max
max
 |  |
 0 х1 х0 х2 х
0 х1 х0 х2 х
х0 – називається точкою min, якщо значення функції в цій точці є найменшими в порівнянні із значенням функції в декому околі точки х0.
 у
у

 min
min
 |
0 х1 х0 х2 х
Необхідна умова існування екстремума (але не достатня).
Якщо в точці х0 існує екстремум, то в цій точці похідна дорівнює 0 або не існує.
Ці точки називаються критичними (або стаціонарними).
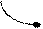
 y Геометрично: дотична в точці
y Геометрично: дотична в точці
max екстремуму паралельна осі Ох.
 |
 min
min
 |
0 x0 x1 x
Але критичні точки не обов’язково являються точками екстремума.
Достатні умови існування екстремуму.
1) х0 є точкою екстрeмума функції y= f (x), якщо при переході через цю точку похідна змінює знак:
якщо з “+” на “ – “ – точка max;
якщо з “ – “ на “+” – точка min.
2) х0 є точкою екстремума, якщо 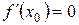 і
і 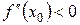 - точка max;
- точка max;
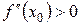 - точка min.
- точка min.
4. Загальна схема дослідження функцій та побудова графіків
І Дослідження функції y = f (x).
1) Область визначення функції, точки розриву, лівостороння і правостороння границі, вертикальні асимптоти.
2) Точки перетину графіка з осями координат.
3) Парність і непарність функції.
4) Похилі асимптоти графіка функції.
ІІ 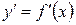
1) Знаходження точок, в яких можливий екстремум (необхідна умова).
2) Достатні умови існування екстремума.
ІІІ 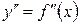
1) Знаходження точок перетину графіка (необхідні умови існування точок перетину).
2) Достатні умови існування точок перетину, інтервали опуклості і вгнутості графіка функції.
IV Поведінка функції на нескінченності, знаходження 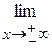 f (x).
f (x).
V Побудова графіка.
Завдання. Методами диференціального числення дослідити функцію і побудувати її графік: 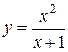
І Область визначення функції:


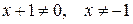
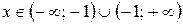 -1
-1
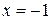 - точка розриву функції.
- точка розриву функції.
Знайдемо односторонні границі:
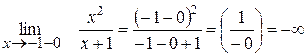
(зліва)
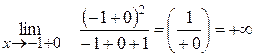
(справа)
Односторонні границі не рівні між собою і не існують, значить в точці х= -1 функція має розрив другого роду.
х =-1 – рівняння вертикальної асимптоти.

 х=-1 у Асимптота – пряма лінія, до якої
х=-1 у Асимптота – пряма лінія, до якої
наближається графік функції, але не перетинає її.
 |
-1 0 х
Асимптоти бувають вертикальні, похилі і горизонтальні.
2) З віссю Оу: при х=0 у (0)=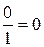 (0; 0)
(0; 0)
З віссю Ох: при у=0 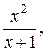
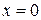 (0; 0)
(0; 0)
3) Якщо f (-x) = f (x), то функція парна (графік симетричний відносно осі Оу).
Якщо f (-x) = -f (x), то функція непарна (графік симетричний відносно початку координат).
Якщо 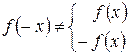 , то функція ні парна, ні непарна.
, то функція ні парна, ні непарна.
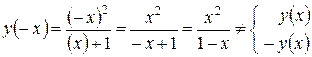 - функція ні парна, ні непарна.
- функція ні парна, ні непарна.
4) Похилі асимптоти.
Рівняння похилих асимптот шукаємо у вигляді у=kx+b,
де k -=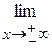
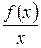 , b=
, b=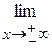
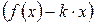 .
.
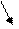
 k=
k=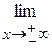
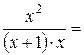
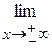
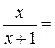
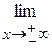
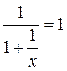


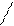 b=
b=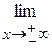
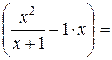
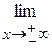
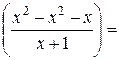
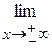
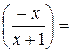
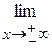
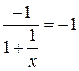
у=х-1 – рівняння похилої асимптоти.
 | |||
 | |||
 х=-1 у у=х-1
х=-1 у у=х-1

 -1 0 1 х
-1 0 1 х

 -1
-1
ІІ 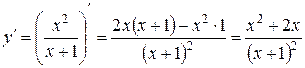
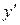 =0
=0 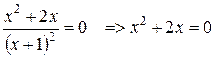
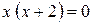
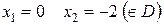
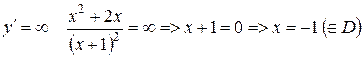




 Знайдемо інтервали монотонності:
Знайдемо інтервали монотонності:



 -2 -1 0 х
-2 -1 0 х
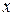
| 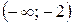
| - 2 | (- 2; -1) | (-1; 0) | 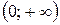
| |
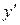
| + | - | - | + | ||
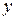
| 
| - 4 | 
| 
| 
|
max min
ІІІ 1) 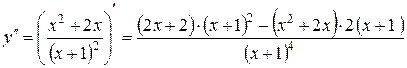 =
=

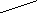

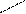
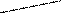 =
=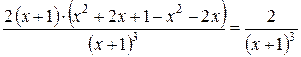
2) Точкою перетину називається точка, яка відділяє опуклу частину графіка від вгнутої.
 у
у
 А А – точка перетину
А А – точка перетину
 |
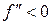
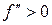
 0 х0 х
0 х0 х
Необхідні умови існування точки перетину
Якщо в точці х 0 є перегин, то в цій точці 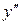 або дорівнює 0, або не існує.
або дорівнює 0, або не існує.
Якщо на деякому інтервалі 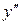 < 0, то на цьому інтервалі графік функції опуклий; якщо
< 0, то на цьому інтервалі графік функції опуклий; якщо 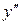 > 0 – графік функції вгнутий.
> 0 – графік функції вгнутий.
 Знайдемо точки, в яких може бути перегин:
Знайдемо точки, в яких може бути перегин: 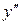 =0
=0 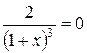 коренів немає
коренів немає 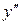 =
=
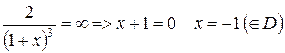
Точок перегину немає.
 3) Знайдемо інтервал опуклості і вгнутості:
3) Знайдемо інтервал опуклості і вгнутості:

 -1 х
-1 х
| х | (-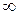 ; -1) ; -1)
| (-1; +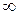 ) )
|
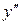
| - | + |
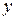
|   опуклий
опуклий
| вгнутий
|
IV Поведінка функції на нескінченності.


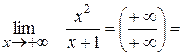
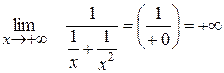
0 0
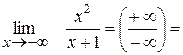
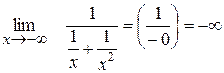
0 02
Горизонтальним асимптот функція не має (якщо k=0, то b=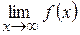 , тому у=b – рівняння горизонтальної асимптоти).
, тому у=b – рівняння горизонтальної асимптоти).
V Побудова графіка.
1) Будуємо асимптоти, точки екстремума і точки перетину, точки перетину графіка з осями координат.
2) Вітки графіка в інтервалах, де функція зростає і спадає, а також інтервали опуклості і вгнутості графіка.


 у
у


 0 х
0 х
 -1
-1
 | |||
 | |||
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 393; Нарушение авторских прав?; Мы поможем в написании вашей работы!