П Л А Н. 2. Самостійна робота №11 “Метод найменших квадратів” (3 год.)

Завдання додому

1. Конспект; [2] с. 408-414.

2. Самостійна робота №11 “Метод найменших квадратів” (3 год.)

[2] с. 420-425.

3. Самостійна робота №12 “Умовний екстремум функції Z=f (x; y) в економічній

теорії» (3 год.) [2] с. 417-420

Питання для самоконтролю

1. Похідна за напрямом.

2. Градієнт.

Л Е К Ц І Я 18

Тема: Екстремум та умовний екстремум функції багатьох змінних.

Мета: сформувати поняття екстремуму та умовного екстремуму функції двох змінних.

Література: [1, с.320-327]; [6, с.313-326].

1. Екстремум функції z=f (x; y). Необхідні і достатні умови існування екстремуму.

2. Поняття про скалярне поле.

1. Розглянемо функцію z=f (x; y), (х; у) .

Означення. Точка Р₀ (х₀; у₀) називається точкою max (min) функції z=f (x; y), якщо існує такий окіл точки Р₀, що належить області визначення 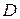, що значення функції в довільній точці цього околу будуть меншими (більшими) значення функції в точці Р₀.

z max

min

y

P₀

х P₀

Необхідні умови існування екстремуму.

z=f (x; y), (х; у) , Р₀ (х₀; у₀) .

Якщо в точці Р₀ існує екстремум, то в цій точці частинні похідні або дорівнюють нулю, або не існують.

Точки, в яких частинні похідні дорівнюють нулю, називаються стаціонарними; точки, в яких частинні похідні дорівнюють нулю або не існують, називаються критичними.

Приклад: Знайти стаціонарні точки функції .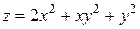

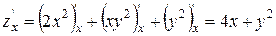
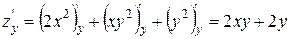
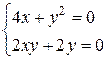
Відповідь: М₁ (-1; 2), М₂ (-1; -2), М₃ (0; 0)

Достатні умови існування екстремуму

Нехай в точці Р₀ (х₀; у₀) існують неперервні похідні першого та другого порядку. Позначимо А =(Р₀), В=(Р₀), С=(Р₀). Тоді:

Якщо АС-В²<0 – екстремум існує;

А >0 (C>0) – min

A <0 (C<0) – max

Якщо АС-В²>0 – екстремум не існує;

Якщо АС-В²=0 – потрібні додаткові дослідження для визначення екстремуму.

Приклад: Знайти екстремум для попередньої функції.

=4 =2у = 2х + 2

1) для М₁ (-1; 2) А = (М₁)=4

В =(М₁)=4

С= (М₁)=0

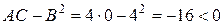- екстремуму немає

2) для М₂ (-1; -2) А=4 В =-4 С=0

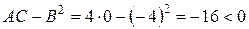- екстремуму немає

3) для М₃ (0; 0) А=4 В=0 С=2

- екстремум існує; так як А=4>0 - min

Z_min = (0; 0)=0

z

(0; 0; 0) у

х

2. Нехай кожній точці простору ставиться у відповідність функція, яка залежить від координат точки: u=u (х; у; z)

Значення цієї функції змінюється від точки до точки.

Тоді таке поле називається скалярним просторовим полем

Нерівномірно нагрітий камінь – це поле температур.

Задати поле – значить задати скалярну функцію в кожній точці цього поля.

Якщо поле плoське, то функція залежить від двох змінних u=u (х; у).

Означення. Нехай дано просторове поле u=u (х; у; z). Множина точок, в яких функція u=u (х; у; z) має постійне значення називається поверхнею рівного рівня поля.

u=u (х; у; z)=с, с=const.

Якщо поле плоске u=u (х; у), то лінія рівного рівня називається геометричним місцем точок, в яких функція постійна.

u=u (х; у)=с, с=const – рівняння лінії рівня.

Приклад: и=х²+у² – поле. Скласти рівняння ліній рівня і побудувати їх.

х²+у² =с

1) с>0, c=R² х²+у² =R² -це рівняння задає множину концентричних кіл різних радіусів.

у

С₃ 2) с=0 х²+у² =0 - точка

С 3) с<0, C= - R² х²+у² =-R² - кола

уявного радіуса

х

Питання для самоконтролю

1. Похідна за напрямом.

2. Градієнт.

Л Е К Ц І Я 19

Тема: Первісна функція та невизначений інтеграл.

Мета: сформувати поняття первісної функції та невизначеного інтеграла;

ознайомити з властивостями невизначеного інтеграла, таблицею основних інтегралів, інваріантністю формули інтегрування.

Література: [1, с. 330-336]; [6, с. 337-342].

Дата добавления: 2014-01-04