Тема: Чисельні методи безумовної мінімізації функції багатьох змінних

Розглядаються задачі безумовної оптимізації 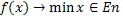(1)

На сьогоднішній день розроблено та досліджено велика кількість методів безумовної мінімізації функції багатьох змінних. І ця область екстремальних задач продовжує зростати.

Буде розглянуто:

1) З методів «0» порядку – метод координатного спуску;

2) З методів «1» порядку – градієнтний метод;

3) З методів «2» порядку метод Ньютона.

Методи 1-го та 2-го порядку явним чином засновані на ідеї заміни мінімізації функції в області чергової точки x_k, першими членами її розкладу для Тейлора.

В градієнтному методі береться лінійна частина розкладення.

В методі Ньютона - квадратична частина – це ідея апроксимації функції.

Загальна схема ітераційних методів для рішення задач безумовної мінімізації функції.

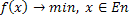(1)

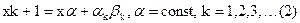
β_k – напрямок зменшення функції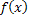

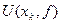множина напрямків зменшення функції 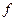, тобто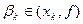

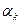- параметр регулюючої довжину кроку вздовж β_k.

Методи монотонного спуску – коли:

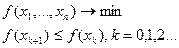(*) називаються релаксаційними.

Якщо функція 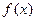диференційована в точці 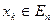, то релаксаційність методу (*), тоді коли напрямок 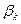утворює не тупий кут з напрямком градієнта

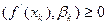
Розглянемо основні властивості градієнту функції 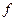в т.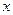

Нехай функція 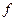диференційована в т. 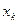, і нехай в цій точці 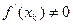, найбільшого зростання функції 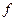в цій точці співпадає з напрямком градієнту в даній точці, а напрямок антиградієнту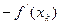

Доведення: з диференційованості 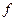в точці 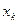слідує, що

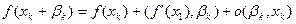(3)

Якщо 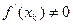тоді при достатньо малих 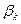головна лінійна частина приросту (3) буде визначатися диференціалом функції:

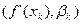
Справедлива нерівність:

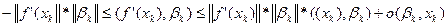(3)

Причому, якщо: 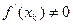тоді права нерівність перетвориться в рівність, лише при

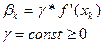
З цього слідує, що при 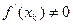напрямок найшвидшого приросту функції в точці 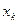співпадає з напрямком градієнта , а напрямок найшвидшого спадання – з напрямком антиградієнта –

Умови зупинки ітераційного процесу (критерій закінчення рахунку)

На практиці часто застосовують наступні умови зупинки:

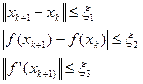(4)

(5)

(6)

Ці умови ґрунтуються на понятті абсолютної похибки.

До початку обчислень прибирається одна з умов (4-6) и відновідну їй мале додатне число .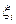

Обчислення закінчуються після 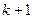кроку, якщо вперши виконується умова зупинки.

На практиці критерій, що складається в одночасному виконанні двох із умов (4-6) або всіх трьох одразу.

Критерій (6) – відноситься лише до задачі безумовної оптимізації. Його виконання означає, що в точці 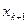з точністю до виконується умова стаціонарності.

Замість критеріїв (4-6) заснованих на поняттях абсолютної похибки, можна використати критерій заснований на понятті відносної похибки:

Метод координатного спуску

В практичних задача оптимізації нерідко зустрічаються випадки, коли мінімізуюча функція або не володіє необхідною гладкістю, або є гладкою.

Проте обчислення її похідних з необхідною точністю потребує надто великого об’єму роботи, в таких випадках можуть бути корисними методи нульового порядку – методи, які не потребують обчислення змінних.

Одним з них є метод координатного спуску(МКС).

Опис методу

Позначимо

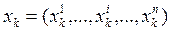
В МКС в якості напряму спуску 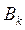використовується один з координатних векторів:

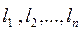
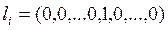
(нульовий вектор, і лише і -й елемент – одиниця)

Отже в точці 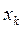зміниться лише одна з компонент.

В схемі метода розрізняють внутрішні та зовнішні ітерації.

Нехай 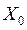- деяке початкове наближення.

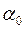- деяке вагоме число

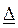- застосовується для факту позначення

Тоді по методу координатного спуску для k =1

(7)

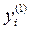позначимо через (першої ітерації).

За формулами (7) буде здійснено спуск за n (розмірність 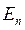) внутрішніх ітерацій з точки 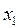в точку 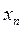по ломаній, що складається з відрізків та прямих паралельних осям координат.

Рис. Одна зовнішня ітерація МПКС для n =2

Спуск за всіма n координатами по функціям (7) складає одну зовнішню першу ітерацію.

Друга зовнішня ітерація здійснюється за формулами:

k =2

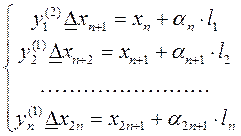
І так далі.

Нехай:

k – номер чергової зовнішньої ітерації;

і – номер і -координати за котрою відбувається спуск(тобто номер внутрішньої ітерації)

Тоді ітераційна рекурентна формула, яка визначає наступне наближення до точки мінімуму, матиме вид:

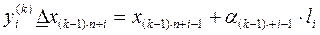
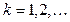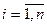; (8)

Після i = n лічильник числа зовнішніх операцій k збільшується на 1, а i =1. Ітераційний процес (8) буде продовжуватися до тих пір, доки:

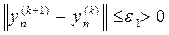
Існують різноманітні способи вибору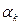. Основна задача при виборі 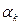в релаксаційних процесах – мінімізація, щоб забезпечити виконання нерівності:

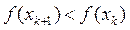
Розглянемо деякі способи вибору параметру 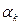в МПКС.

Спосіб 1: вибір параметру 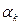з умови мінімізації функції вздовж напряму

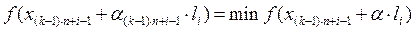(9)

Спосіб 2: нехай 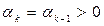, обчислимо значення функції в точці 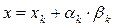, тоді

(10)

Якщо нерівність (10) виконується, то або приймемо, що 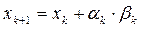,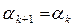та перейдемо до наступної k +2 ітерації, або оберемо 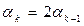, якщо значення 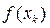менше його минулого значення, то процес подвоєння можна продовжувати до тих пір, доки зменшення не зупиниться, тобто буде виконуватись нерівність (10).

В тому випадку, якщо нерівність (10) не виконується, то обчислимо значення функції в точці 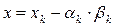та перевіримо нерівність

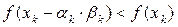(11)

В випадку виконання задачі (11), або приймемо

,

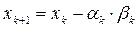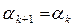
або оберемо, як в минулому випадку 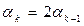, доки виконується нерівність(11).

Назвемо ітерацію k+1 успішною, якщо справедливо хоча б одне з нерівностей (10)-(11).

Якщо за одну зовнішню ітерацію, яка складається з n – внутрішніх з вибором усіх координатних осей Е₁ та Е_n, з кроком α_k реалізувалась хоча б одна успішна ітерація, то довжина кроку α_k не ділиться і зберігається на протязі усього циклу з n – ітерацій.

Якщо серед останніх n - ітерацій не виявилось ні одної успішної, тоді крок α_k ділиться на 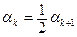і переходить до наступного циклу.

Найпростіший варіант цього методу

На початку пошуку задаються дві точки: 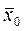і 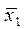, з яких проводиться спуск, за допомогою будь-якого варіанту градієнтного методу. І отримують дві точки: х₀ та х₁. Потім отримують:

,

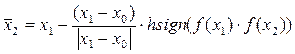де h – додатна константа, яка називається часовим кроком.

З точки 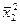, краї, загалом знаходяться на «схилі оврагу» проводить спуск за допомогою градієнтного методу та визначають наступну точку х₂ на «дні оврагу».

А якщо з відомих точок (х₀, х₁,…,х _k), k>2, тоді

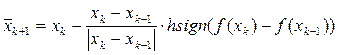
Здійснюючи спуск за допомогою градієнтного методу, знаходимо наступну точку х _k+1 на «дні оврагу».

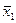
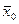
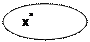
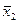
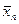х₂ х₁ х₀

х₃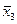

Величина кроку h підбирається емпірично з урахуванням інформації про мінімізуючи функцію, яку отримали у ході пошуку мінімуму.

Від правильного вибору h залежить швидкість сходження методу, якщо крок h – великий, то на крутих поворотах оврага точки 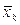можуть занадто віддалятися від дна оврага. І спуск з точки 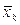у точку х _k може вимагати більшої кількості розрахунків, крім того при великих h на крутих поворотах може відбутися вибір точки 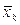з оврагу і правильний напрям нової точки мінімуму буде втрачено.

Якщо крок h занадто малий, то пошук може дуже вповільнитись і ефект від застосування овражного методу може бути незначним.

Дата добавления: 2014-01-04