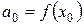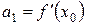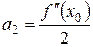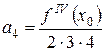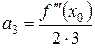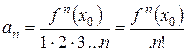Теорема Абеля

Якщо степеневий ряд збіжний при 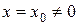, то він абсолютно збіжний для всіх значень х, що задовольняють нерівність 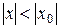, тобто збіжний на інтервалі 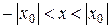. Такий інтервал називається інтервалом збіжності ряду, а число 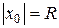називається радіусом збіжності степеневого ряду.

розб збіг розб

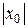0 х

Інтервал збіжності можна записати у вигляді (- R; R)

Метод знаходження інтервала збіжності степеневого ряду

Нехай дано степеневий ряд 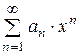. Для знаходження інтервала збіжності застосовують ознаку Д’Аламбера.

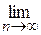
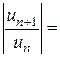
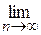
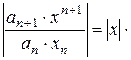
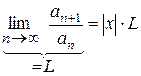
Для того, щоб ряд був збіжним, потрібно, щоб одержаний вираз був меншим 1, тобто

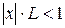
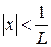
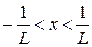- інтервал збіжності ряду

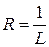
Для знаходження області збіжності потрібно дослідити поведінку ряду на кінцях інтервалу. Для цього замість х в степеневий ряд підставляють значення 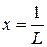і 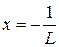і досліджують одержані числові ряди на збіжність.

Приклад: знайти область збіжності степеневого ряду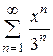

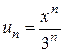
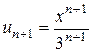
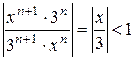
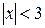
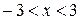- інтервал збіжності

R = 3

Перевіримо поведінку ряду на кінцях інтервалу:

а) при х = 3 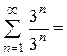не виконується необхідна ознака збіжності, тобто 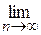1=1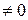, отже ряд розбіжний.

Значить правий кінець інтервалу не входить в область збіжності.

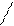
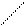б) при х = - 3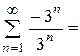

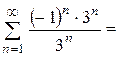
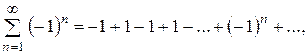
одержали ряд, знаки якого строго чергуються; застосуємо ознаку Лейбніца:

1 = 1=1 =... – модулі членів ряду не спадають, значить ряд розбіжний.

Тобто, лівий кінець інтервалу не входить в область збіжності.

Відповідь: областю збіжності степеневого ряду є інтервал (- 3; 3)

розб збіг розб

- 3 0 3 х

2. Розглянемо степеневий ряд за степенями :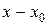

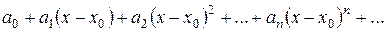
Нехай функція f (x) є сумою ряду на інтервалі :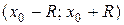

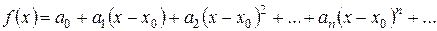
Нехай існують всі похідні функції f (x) і значення самої функції в точці 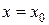. Знайдемо коефіцієнти цього ряду, послідовно диференцюючи ряд і підставляючи в знайдені похідні значення .

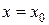Знайдемо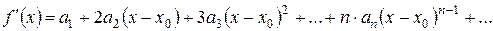

...

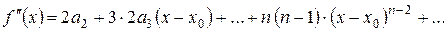
Тоді

Степеневий ряд прийме вигляд:

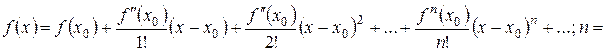0, 1, 2,... – ряд Тейлора.

Теорема (про достатні умови розкладання функції в ряд Тейлора)

Якщо функція f (х) в інтервалі 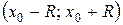має похідні всіх порядків та існує число M > 0 таке, що модуль кожної похідної буде меншим від М.

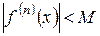, то функцію f (x) можна розкласти в ряд Тейлора.

Якщо в ряді Тейлора приймемо 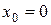, то одержимо ряд Маклорена:

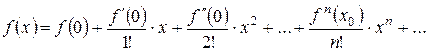
Степеневі ряди застосовуються для наближених обчислень, для розв’язування диференціальних рівнянь, для обчислення визначених та невизначених інтегралів.

3. Щоб функцію f (x) розкласти в ряд Маклорена, потрібно:

1) знайти похідні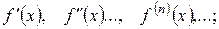

2) обчислити значення похідних в точці х = 0

3) записати ряд Маклорена для даної функції і знайти інтервал його збіжності;

4) визначити інтервал (- R; R) в якому залишковий член формули Маклорена 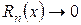при .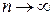

Приклади:

1)

...

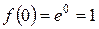
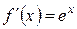
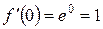
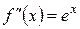
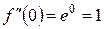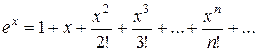
Область збіжності ряду

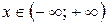
2)

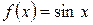
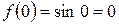
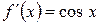
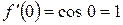
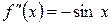
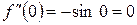
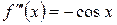
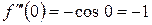
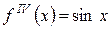
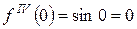
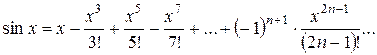
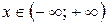
3)

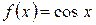
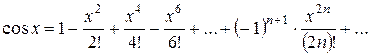
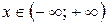
4) Біноміальний ряд

,

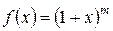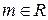
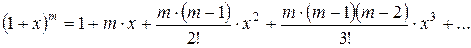
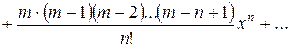
Область збіжності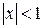

5)

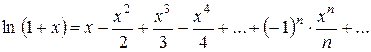
n = 0, 1, 2,...

Область збіжності (-1; 1]

6)

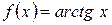
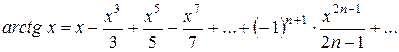
n = 1, 2, 3 …

Область збіжності [ -1; 1]

Дата добавления: 2014-01-04