Функции алгебры логики

Структурно-функциональная схема системы

Структурная схема системы

На структурной схеме каждый элемент сложной системы отображается в виде геометрической фигуры, чаще прямоугольника. Прямоугольники соединяются линиями таким образом, чтобы полученная структурная схема отображала условия работоспособности системы от работоспособности элементов. При этом существуют следующие правила:

1. Последовательное соединение элементов (или групп элементов) обозначает необходимость одновременной работоспособности данных элементов (групп элементов):

В этой схеме элементы 1, 2 и 3 должны быть исправны одновременно.

2. Параллельное соединение элементов (групп элементов) обозначает случай резервирования, т.е. случай, когда для работоспособности системы требуется только часть параллельно соединенных элементов (групп элементов). Здесь возможны разные способы обозначений. Рассмотрим их.

a. Простое параллельное соединение обозначает постоянно включенный резерв. В этом случае существует один основной элемент, а остальные N-1 являются резервными. Все N элементов находятся под нагрузкой и расходуют свой ресурс. Для работоспособности такой системы необходима работоспособность хотя бы одной элемента.

b. Если рядом с параллельным соединением есть обозначение вида m=a/b, это означает случай резервирования с дробной кратностью. Величина m означает отношения количества резервных элементов к количеству основных. Например, в данной схеме 2 основных и 1 резервный элемент. Следовательно, для работоспособности системы необходима работоспособности любых двух из трёх элементов.

c. На следующей схеме приведено обозначение резервирования замещением. Оно обозначает ситуацию, когда резервный элемент находится в выключенном режиме (и не расходует ресурс) и включается только, если выходит из строя основной.

В качестве общего примера рассмотрим следующую структурную схему.

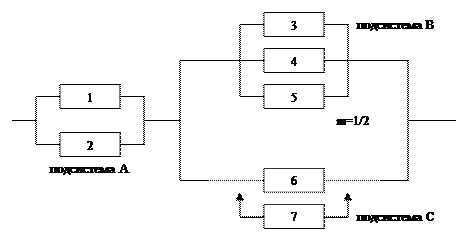
Здесь подсистема A, B и C представляют собой случае различных параллельных (в структурном смысле) соединений элементов: постоянно включенный резерв, постоянно включенный резерв с дробной кратностью и резерв замещением соответственно. Также видно, что подсистемы B и C постоянно резервируют друг друга. При этом одновременно с любой из подсистема B или C должна быть работоспособна система A.

Преимуществом структурной схемы является её высокая наглядность. Но при этом на этой схеме не указано: является ли система ремонтируемой, какова дисциплина обслуживания элементов, количество ремонтных бригад и приоритет обслуживания. Также не указаны показатели надежности элементов. Также следует иметь в виду, что структурная схема не является математической моделью функционирования системы.

Эти недостатки требуют дополнительных описаний условий работоспособности системы, иначе нельзя выполнить анализ системы по критериям надежности.

На структурно-функциональной схеме отображаются элементы и взаимосвязи между элементами. При этом считается, что каждый элемент производит и потребляет ресурсы: энергию, вещество, информацию, управляющее воздействие. Сами элементы обозначаются геометрическими фигурами (кругами, прямоугольниками). Связи между элементами обозначаются стрелками. Разные цвета или начертания стрелок могут обозначают различные ресурсы. Стрелки могут быть однонаправленными или двунаправленными. В последнем случае это означает, что ресурс может передавать по этой связи в обе стороны.

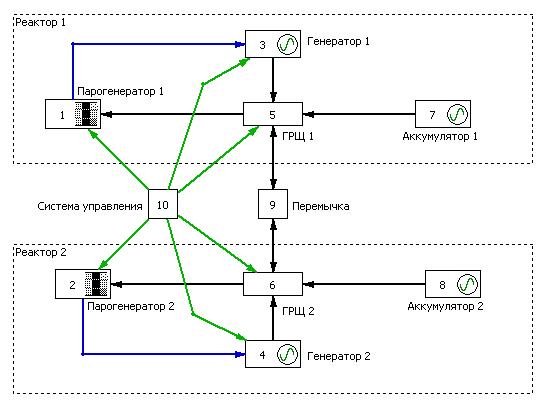
На этом примере представлена система из двух реакторов, соединенных перемычкой и управляемых единой системой управления. Черным цветом обозначена электроэнергия, синим – пар, а зелёным – управляющее воздействие.

Элемент системы считается работоспособным только в том случае, если он исправен и к нему обеспечено поступление всех необходимых ресурсов. Если какой-либо ресурс представлен несколькими источниками (например, генератор, перемычка и аккумулятор – источники энергии на ГРЩ), то эти источники считаются альтернативными и резервированными.

Преимущество структурно-функциональной схемы на структурной состоит в том, что она показывает взаимосвязи между элементами, а не только их общий вклад в надежность системы. Это позволяет выявлять зависимые отказы и условия работоспособности элементов от состояния других элементов.

В то же время на СФС отсутствует информация о надежности элементов, об их условия восстановления и т.д.

Пусть система состоит из N элементов. Будем считать, что каждый элемент может находиться либо в исправном, либо отказовом состоянии. Для этого с каждым элементом свяжем булеву (логическую) переменную 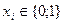. При этом, если 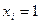, то элемент исправен. А если 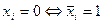, то элемент находится в состоянии отказа.

Составим вектор состояния системы 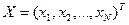. Тогда зависимость работоспособности системы от состояния элементов можно представить в виде функции алгебры логики (ФАЛ) 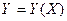. Эта функция называется функцией работоспособности системы (ФРС) и может принимать в зависимости от разных значение X, значения ноль (система неработоспособна) и единица (система работоспособна). В ФАЛ булевы переменные 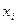связываются вместе с помощью операции конъюнкции (логическое умножение), дизъюнкции (логическое сложение) и инверсии (логическое отрицание).

Пусть некоторая система описывается структурной схемой:

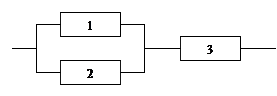
Тогда ФРС может быть представлена в виде:

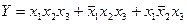
Используя правила алгебры логики это выражение может быть упрощено:

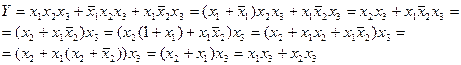
Зная ФРС можно сразу определить работоспособно данное состояние системы или нет.

Инверсия ФРС называется функцией неработоспособности системы:

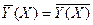
Для нашего примера ФНС будет иметь вид:

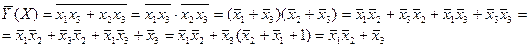
ФРС и ФНС можно считать математической моделью функционирования системы в смысле её надежности. Но снова здесь никак не указана информация о ремонтируемости системы, показатели надежности системы и другая важная информация. Но если эта информация предоставлена, то от ФАЛ можно перейти к выражениям для вычисления критериев надежности всей системы.

Дата добавления: 2014-01-03