Волны в упругих средах

Волной называется распространение колебаний в пространстве с течением времени. При распространении волны частицы среды волной не увлекаются, но происходит перенос энергии от источника колебаний к точкам среды.

В поперечной волне частицы среды совершают колебания в направлении, перпендикулярном направлению распространения волны. Такие волны могут распространяться в средах, в которых возможна деформация сдвига (т.е. в твердых телах и на поверхности жидкостей). Пример поперечной волны - волна на поверхности жидкости.

В продольной волне частицы среды совершают колебания в направлении распространения волны. Такие волны распространяются в средах, в которых возможна деформация сжатия и разряжения (т.е. и в твердых телах, и в газах, и в жидкостях). Пример продольной волны - звук.

Характеристики волн:

1) фронт волны - геометрическое место точек среды, до которых дошло колебание в данный момент времени. В зависимости от формы фронта волны бывают сферические, цилиндрические, плоские волны;

2) фазовая скорость V - скорость распространения в пространстве данной фазы колебаний;

3) длина волны l - наименьшее расстояние между двумя точками среды, совершающими колебания в одинаковой фазе. Численно длина волны равна расстоянию, на которое перемещается фронт волны за время, равное периоду колебаний

l = V×T; (5.105)

4) волновой вектор .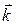

Модуль волнового вектора (называется волновым числом)

. (5.106)

По направлению волновой вектор совпадает с направлением распространения волны. Волновое число можно выразить через циклическую частоту колебаний частиц среды :

. (5.107)

Уравнение волны определяет смещение от положения равновесия x точек среды, находящихся на расстоянии x от источника колебаний. Запишем уравнение плоской монохроматической волны, распространяющейся в положительном направлении оси x. Пусть источник находится в начале координат и совершает колебание по закону

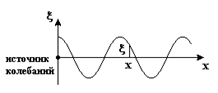x(0, t) = A cosw t. (5.108)

На расстоянии x от источника колебаний спустя некоторое время благодаря упругой связи между частицами среды возникнут колебания с той же частотой, той же амплитудой (если среда не поглощает энергию), что и в источнике, но эти колебания будут отставать по фазе от колебаний в источнике, т.к. волне нужно время, чтобы пройти расстояние x (см. рис. 5.32)

x(х, t) = A cos w (t-t ¢^¢), (5.109)

где .

С учетом этого

. (5.110)

Если учесть (5.107), то

x (x, t) = A cos (w t - kx). (5.111)

Мы получили уравнение плоской монохроматической волны, распространяющейся в положительном направлении оси Ох. Если волна распространяется в противоположном направлении, то

x (х, t) = A cos (w t + kx). (5.112)

Если плоская монохроматическая волна распространяется в произвольном направлении, то уравнение волны имеет вид:

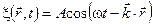, (5.113)

где 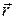- радиус - вектор данной точки пространства.

Уравнение волны является решением дифференциального уравнения второго порядка, называемого волновым:

. (5.114)

Решение волнового уравнения зависит от дополнительных условий, и в зависимости от них в качестве решения можно получить уравнение плоской, сферической или цилиндрической волны.

Зная уравнение волны, можно найти скорость и ускорение частиц среды в любой момент времени:

, (5.115)

. (5.116)

Дата добавления: 2014-01-04