
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Незатухающие механические и электромагнитные колебания. Сложение колебаний
|
|
|
|
2.1. Примеры решения задач
Пример 1
Материальная точка массой m = 10 г совершает гармонические колебания по закону синуса с периодом T = 2 с и начальной фазой, равной нулю. Полная энергия колеблющейся точки W = 0,1 мДж.
Найти: 1) амплитуду колебаний; 2) написать уравнение данных колебаний;
3) найти наибольшее значение силы Fmax, действующей на точку.
| Дано: m = 10 г = 0,01 кг T = 2 с W = 0,1 мДж = 0,1х10-3 Дж |
| A -? F max -? |
Решение: Уравнение гармонических колебаний имеет вид
 .
.
По условию задачи начальная фаза равна нулю, следовательно
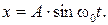
Взяв первую производную смещения по времени, найдем скорость колеблющейся точки
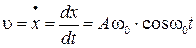 .
.
Кинетическая энергия колеблющейся точки
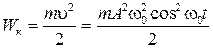
Полная энергия колеблющейся точки равна максимальному значению ее кинетической энергии
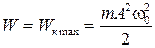
Отсюда находим следующее выражение для амплитуды колебаний
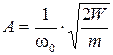
Циклическая частота связана с периодом колебаний соотношением
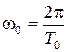
Подставляя его в выражение для амплитуды, получаем
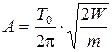 ,
,
 м.
м.
Найдем численное значение частоты
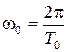 ,
, 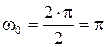
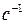 .
.
Запишем уравнение гармонических колебаний для данной точки
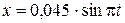 , м
, м
Согласно второму закону Ньютона
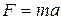 (1)
(1)
Ускорение колеблющейся точки найдем, взяв вторую производную смещения по времени (или, что то же самое, первую производную от скорости по времени)
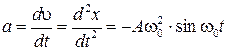
Отсюда максимальное ускорение
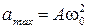 .
.
Подставив это выражение максимального ускорения в соотношение (1), найдем максимальную силу, действующую на точку,
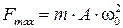 .
.
Произведем вычисления
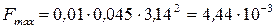 Н.
Н.
Ответ: 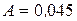 м;
м; 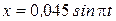 , м;
, м; 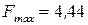 мН.
мН.
Пример 2
Написать уравнение гармонического колебательного движения, происходящего по закону синуса, если максимальное ускорение точки см/с2, период колебаний
см/с2, период колебаний 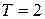 с и смещение точки от положения равновесия в начальный момент времени
с и смещение точки от положения равновесия в начальный момент времени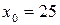 мм.
мм.
Дано:
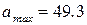 см/с2
T = 2 с см/с2
T = 2 с
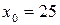 мм мм
|
| Уравнение г.к.-? |
Решение: Смещение точки изменяется с течением времени по закону
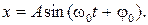
1). Зная период колебаний, находим циклическую частоту
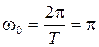 c-1.
c-1.
2). Найдем, как изменяется с течением времени ускорение материальной точки. Для этого надо установить зависимость скорости точки от времени, а затем продифференцировать эту зависимость по времени
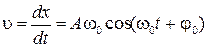 , а
, а
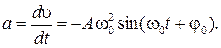
Ускорение будет максимальным при 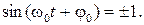
Таким образом, 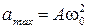 ,откуда следует, что
,откуда следует, что
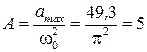 см.
см.
3). Начальную фазу 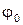 найдем из условия, что в начальный момент времени
найдем из условия, что в начальный момент времени 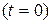 смещение от положения равновесия
смещение от положения равновесия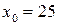 мм:
мм:
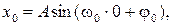
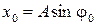 , откуда находим, что
, откуда находим, что
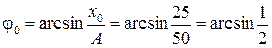 ,
,
т.е. 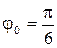
Подставив полученные значения амплитуды, циклической частоты и начальной фазы в уравнение колебаний, получим искомое уравнение гармонического колебания
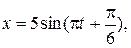 см.
см.
Ответ: 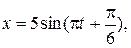 см.
см.
Пример 3
Найти отношение кинетической энергии 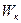 точки, совершающей гармонические колебания по закону синуса к ее потенциальной энергии
точки, совершающей гармонические колебания по закону синуса к ее потенциальной энергии 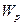 для моментов времени
для моментов времени 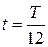 . Начальная фаза колебаний
. Начальная фаза колебаний 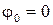 .
.
Дано:
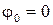
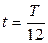
|
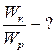
|
Решение: Так как начальная фаза колебаний 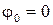 , то уравнение смещения точки от положения равновесия примет вид
, то уравнение смещения точки от положения равновесия примет вид
 .
.
Тогда скорость точки изменяется по закону
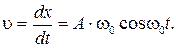
Кинетическая энергия точки 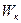 равна
равна

а потенциальная энергия точки, совершающей гармонические колебания, вычисляется по формуле
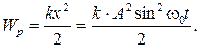
Тогда 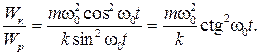
Так как 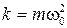 , то получаем, что
, то получаем, что
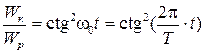 .
.
Найдем отношение 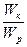 для момента времени
для момента времени 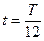 :
:

Ответ: 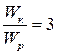 .
.
Пример 4
Найти амплитуду 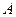 и начальную фазу
и начальную фазу 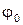 гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями
гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями 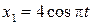 см и
см и 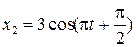 см. Написать уравнение результирующего колебания. Построить векторную диаграмму сложения амплитуд.
см. Написать уравнение результирующего колебания. Построить векторную диаграмму сложения амплитуд.
Дано:
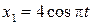 см см
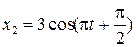 см см
|
| Уравнение гармонических колебаний -? |
Решение: Так как складываются два одинаково направленных гармонических колебания одинаковой частоты 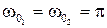 c-1, то результирующее колебание будет иметь ту же частоту:
c-1, то результирующее колебание будет иметь ту же частоту: 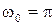 c-1.
c-1.
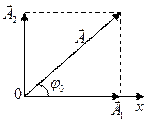 Амплитуду A и начальную фазы результирующего колебания найдем с помощью метода векторных диаграмм. Для этого изобразим графически оба складываемых колебания на векторной диаграмме (см. рисунок).
Амплитуду A и начальную фазы результирующего колебания найдем с помощью метода векторных диаграмм. Для этого изобразим графически оба складываемых колебания на векторной диаграмме (см. рисунок).
Напомним, что для изображения колебания, уравнение которого 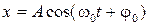 , методом векторных диаграмм необходимо из произвольной точки
, методом векторных диаграмм необходимо из произвольной точки 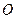 , выбранной на оси
, выбранной на оси  , отложить вектор
, отложить вектор 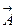 , длина которого равна амплитуде колебания, причем угол между вектором
, длина которого равна амплитуде колебания, причем угол между вектором 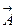 и осью
и осью 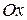 должен быть равен начальной фазе
должен быть равен начальной фазе 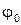 колебания.
колебания.
В нашей задаче начальная фаза первого колебания 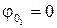 , поэтому вектор
, поэтому вектор 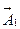 откладывается вдоль оси
откладывается вдоль оси  , причем его длина
, причем его длина 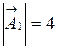 см.
см.
Так как 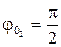 , то вектор
, то вектор 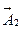 откладывается перпендикулярно оси
откладывается перпендикулярно оси 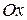 и его длина равна
и его длина равна 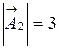 см. Амплитуда результирующего колебания
см. Амплитуда результирующего колебания 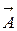 равна
равна 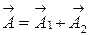 .
.
Величину амплитуды найдем по теореме Пифагора
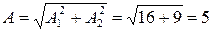 см.
см.
Из рисунка видно, что 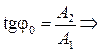 начальная фаза
начальная фаза 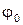 равна
равна
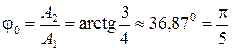 рад.
рад.
Таким образом, уравнение результирующего колебания будет иметь вид 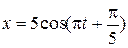 см.
см.
Ответ: 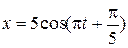 см.
см.
Пример 5
Складываются два колебания одинакового направления, выражаемых уравнениями x 1= A 1cosw(t +t1), x 2= A 2cosw(t +t2) где, A 1=1см, A 2=2см, t1=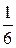 c, t2=
c, t2=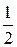 c, w=p c-1. Определить начальные фазы
c, w=p c-1. Определить начальные фазы 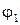 и
и 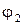 составляющих колебаний, найти амплитуду
составляющих колебаний, найти амплитуду 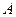 и начальную фазу
и начальную фазу 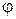 результирующего колебания. Написать уравнение результирующего колебания.
результирующего колебания. Написать уравнение результирующего колебания.
Дано:
x 1= A 1cosw(t +t1)
x 2= A 2cosw(t +t2)
A 1=1см
A 2=2см
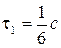
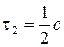 w=p c-1
w=p c-1
|
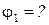 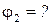 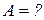 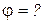 Уравнение результирующего колебания -?
Уравнение результирующего колебания -?
|
Решение: Уравнение гармонического колебания имеет вид:
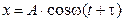 .
.
Преобразуем уравнения, заданные в условия задачи, к такому же виду: 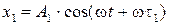 , (1)
, (1)
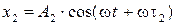 (2)
(2)
Из сравнения выражений (2) с равенством (1) находим начальные фазы первого и второго колебаний:
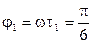 рад;
рад;
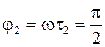 рад.
рад.
Для определения амплитуд 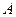 и начальной фазы
и начальной фазы  результирующего колебания воспользуемся методом векторных диаграмм.
результирующего колебания воспользуемся методом векторных диаграмм.
На рисунке построена векторная диаграмма по данным задачи
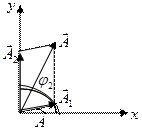 |
Согласно теореме косинусов амплитуда результирующего колебания определяется соотношением
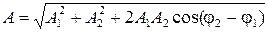 (3)
(3)
Подставив значения 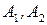 и
и 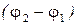 в соотношение (3), произведем вычисления
в соотношение (3), произведем вычисления
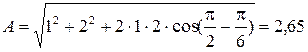 см.
см.
Тангенс начальной фазы 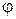 результирующего колебания определим по соотношению
результирующего колебания определим по соотношению
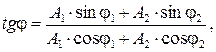
откуда начальная фаза
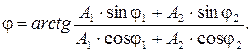
Подставив значения 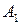 ,
,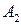 ,
,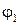 ,
,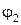 произведем вычисления
произведем вычисления
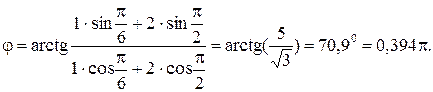
Так как циклические частоты складываемых колебаний одинаковы, то результирующее колебание будет иметь ту же частоту  . Это позволяет написать уравнение результирующего колебания в виде.
. Это позволяет написать уравнение результирующего колебания в виде.
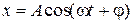 , (4)
, (4)
где 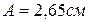 ,
, 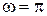
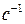 ,
,  рад.
рад.
Подставляя значения 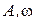 и
и  в (4), получаем уравнение результирующего колебания
в (4), получаем уравнение результирующего колебания
 , см.
, см.
Ответ: 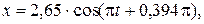 см.
см.
Пример 6
Точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, заданных уравнениями: 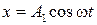 и
и 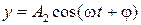 , где
, где 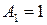 см,
см, 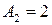 см,
см,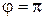 . Найти уравнение траектории точки и построить ее с соблюдением масштаба.
. Найти уравнение траектории точки и построить ее с соблюдением масштаба.
Дано:
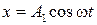
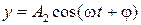
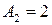 см см
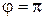
|
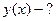
|
Решение: Уравнение траектории результирующего движения точки, получающего при сложении взаимно перпендикулярных колебаний с одинаковыми частотами, имеет вид:
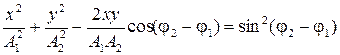
В данном случае 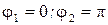 , поэтому
, поэтому 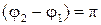 .
.
Подставляя это значение в предыдущее уравнение, имеем 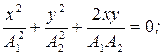
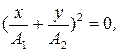
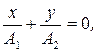
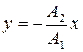 ;
; 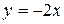 .
.
Видно, что траекторией результирующего движения в данном случае является прямая. Построим ее с соблюдения масштаба.
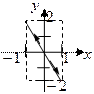
Стрелками указаны направления движения точки по траектории.
Ответ: 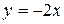
Пример 7
Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых  и
и 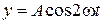 , где
, где 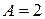 см,
см,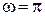
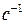 . Найти уравнение траектории точки и построить ее с соблюдением масштаба.
. Найти уравнение траектории точки и построить ее с соблюдением масштаба.
Дано:
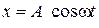
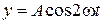
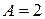 см см
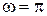 c-1 c-1
|
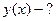
|
Решение: Чтобы найти уравнение траектории точки, исключим время 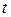 из заданных уравнений. Для этого воспользуемся формулой
из заданных уравнений. Для этого воспользуемся формулой 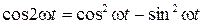 .
.
В данном случае
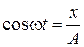 ,
,

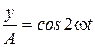 ;
; 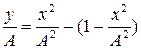 ; отсюда
; отсюда
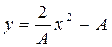 - это уравнение параболы.
- это уравнение параболы.
Подставим 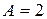 :
: 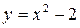
Построим по точкам: 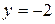 при
при 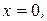
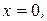
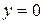 при
при 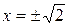 ,
,
ветви параболы направлены вверх.
Стрелками указано направление движения точки.

Ответ: 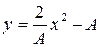 .
.
Пример 8
Колебательный контур состоит из конденсатора емкостью 0,025 мкФ и катушки с индуктивностью 1,015 Гн. Омическим сопротивлением цепи пренебречь. На обкладках конденсатора находится заряд 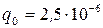 Кл.
Кл.
1). Написать для данного контура уравнения (с числовыми коэффициентами) законы изменения разности потенциалов на обкладках конденсатора и силы тока в цепи от времени.
2). Найти значения разности потенциалов на обкладках конденсатора и силы тока в цепи в момент времени 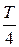 и
и 
Дано:
 Ф Ф
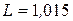 Гн Гн
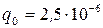 Кл Кл
|
Уравнение?
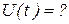 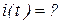
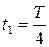 , , 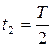
|
Решение: Уравнение изменения заряда на обкладках конденсатора со временем имеет вид
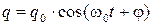 .
.
Начальная фаза колебаний равна нулю, следовательно,
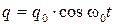
Изменение направления на обкладках конденсатора задается уравнением
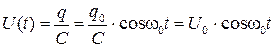 ,
,
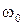 - циклическая частота собственных колебаний в контуре,
- циклическая частота собственных колебаний в контуре,
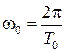 ,
,
где 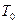 – период собственных колебаний
– период собственных колебаний
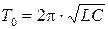
Следовательно, 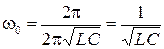 .
.
Чтобы записать с числовыми коэффициентами уравнение изменения разности потенциалов, произведем вычисления:
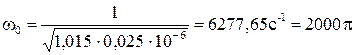 с-1;
с-1;
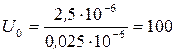 В.
В.
Таким образом, получаем уравнение в виде
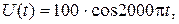 В.
В.
Изменение силы тока со временем задается уравнением
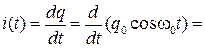
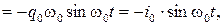
где 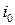 - амплитудное значение силы тока. Рассчитаем эту величину
- амплитудное значение силы тока. Рассчитаем эту величину
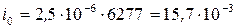 А.
А.
Окончательно получаем уравнение
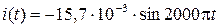 , А.
, А.
Получаем значение разности потенциалов, и силы тока в цепи в момент времени 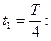
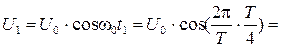
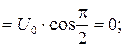
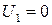
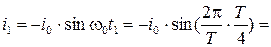
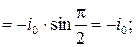
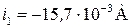
Аналогично для момента времени 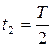 :
:
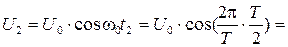
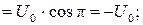
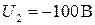 .
.
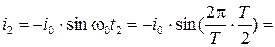
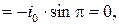
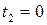
Ответ: 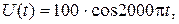 В;
В;
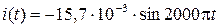 ,А;
,А; 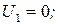
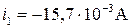 ;
; 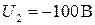 ;
; 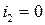 .
.
2.2. Задачи для самостоятельного решения
1.* Точка совершает гармонические колебания по закону синуса. Период колебаний 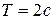 , амплитуда
, амплитуда 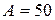 мм, начальная фаза
мм, начальная фаза 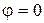 . Найти скорость
. Найти скорость  точки в момент времени, когда смещение точки от положения равновесия
точки в момент времени, когда смещение точки от положения равновесия 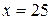 мм.
мм.
( )
)
2. Определить максимальное значение скорости и ускорения точки, совершающей гармонические колебания с амплитудой 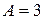 см и угловой частотой
см и угловой частотой 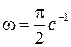 .
.
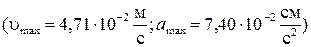
3. Колебания материальной точки происходят согласно уравнению  , где
, где  см,
см, 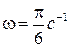 . В момент, когда возвращающая сила достигла значения – 5 мН, потенциальная энергия
. В момент, когда возвращающая сила достигла значения – 5 мН, потенциальная энергия 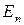 стала равной 100 мкДж. Найти этот момент времени и соответствующую ему фазу колебаний.
стала равной 100 мкДж. Найти этот момент времени и соответствующую ему фазу колебаний.
4. К спиральной пружине подвесили грузик, в результате чего пружина растянулась на 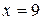 см. Каков будет период
см. Каков будет период  колебаний грузика, если его немного оттянуть вниз и затем отпустить?
колебаний грузика, если его немного оттянуть вниз и затем отпустить?
(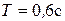 )
)
5. Потенциальная энергия частицы, совершающей гармонические колебания вдоль оси 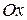 по закону косинуса, в момент времени
по закону косинуса, в момент времени 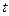 больше ее кинетической энергии в
больше ее кинетической энергии в 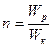 раза. Найти
раза. Найти 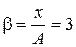 – отношение координаты частицы к амплитуде ее колебаний в этот момент времени.
– отношение координаты частицы к амплитуде ее колебаний в этот момент времени.
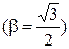
6. Колебания точки происходят по закону 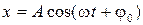 . В некоторый момент времени смещение
. В некоторый момент времени смещение  точки равно 5 см, ее скорость
точки равно 5 см, ее скорость 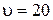 см/с и ускорение
см/с и ускорение 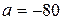 см/с2. Найти амплитуду
см/с2. Найти амплитуду 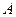 , угловую частоту
, угловую частоту  , период колебаний
, период колебаний 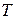 и фазу
и фазу 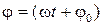 в рассматриваемый момент времени.
в рассматриваемый момент времени.
(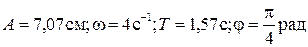 )
)
7. Складываются два гармонических колебания одного направления с одинаковыми периодами 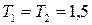 c и амплитудами
c и амплитудами 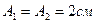 . Начальные фазы колебаний
. Начальные фазы колебаний 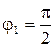 рад и
рад и 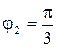 рад. Определить амплитуду и начальную фазу результирующего колебания. Найти его уравнение и построить с соблюдением масштаба векторную диаграмму сложения амплитуд.
рад. Определить амплитуду и начальную фазу результирующего колебания. Найти его уравнение и построить с соблюдением масштаба векторную диаграмму сложения амплитуд.
(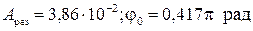 )
)
8. Складываются три гармонических колебания одного направления с одинаковыми периодами 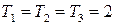 с и амплитудами
с и амплитудами 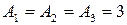 см. Начальные фазы колебаний
см. Начальные фазы колебаний 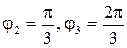 . Построить векторную диаграмму сложения амплитуд. Определить из чертежа амплитуду
. Построить векторную диаграмму сложения амплитуд. Определить из чертежа амплитуду 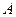 и начальную фазу
и начальную фазу 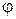 результирующего колебания. Написать его уравнение.
результирующего колебания. Написать его уравнение.
(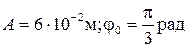 )
)
9. Складываются два гармонических колебания одинаковой частоты и одинокого направления: 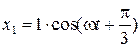 см и
см и 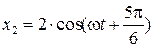 см. Построить векторную диаграмму сложения амплитуд. Определить амплитуду и начальную фазу
см. Построить векторную диаграмму сложения амплитуд. Определить амплитуду и начальную фазу 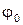 результирующего колебания. Написать уравнение результирующего колебания.
результирующего колебания. Написать уравнение результирующего колебания.
(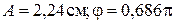 рад)
рад)
10. Материальная точка одновременно участвует в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями 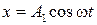 и
и 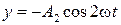 , где
, где 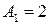 см,
см, 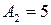 см. Найти уравнение траектории и построить траекторию, показав направление движения точки.
см. Найти уравнение траектории и построить траекторию, показав направление движения точки.
11. Движение точки задано уравнениями 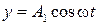 и
и 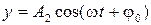 , где
, где 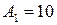 см,
см, 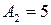 см,
см, 
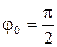 рад. Найти уравнение траектории и построить ее, указав направление движения точки.
рад. Найти уравнение траектории и построить ее, указав направление движения точки.
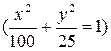
12. Складываются два взаимно перпендикулярных колебания, выражаемые уравнениями 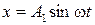 и
и 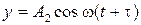 , где A 1=2см, A 2=1см,
, где A 1=2см, A 2=1см, 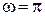
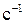 ,
,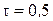 с. Найти уравнение движения и построить траекторию, показав направление движения точки.
с. Найти уравнение движения и построить траекторию, показав направление движения точки.
(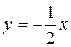 )
)
13. Электроемкость идеального электрического колебательного контура
С = 0,1 нФ. В момент времени 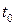 конденсатор был не заряжен, а в катушке индуктивности мгновенно индуцировали ток силой
конденсатор был не заряжен, а в катушке индуктивности мгновенно индуцировали ток силой 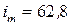 мА, после чего контур предоставили самому себе. В контуре начались незатухающие электромагнитные колебания с периодом
мА, после чего контур предоставили самому себе. В контуре начались незатухающие электромагнитные колебания с периодом 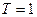 мкс. Полагая, что колебания заряда конденсатора происходят по закону косинуса, найти: индуктивность контура
мкс. Полагая, что колебания заряда конденсатора происходят по закону косинуса, найти: индуктивность контура 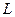 ; начальную фазу
; начальную фазу 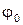 колебаний; момент времени
колебаний; момент времени 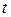 , ближайший к начальному
, ближайший к начальному 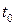 , когда сила тока в контуре впервые после начала колебаний уменьшаются до значения
, когда сила тока в контуре впервые после начала колебаний уменьшаются до значения 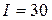 мА.
мА.
(L=0,25 мГн; 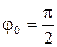 рад;
рад; 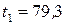 нс)
нс)
14. Катушка с индуктивностью 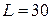 мкГн присоединена к плоскому конденсатору с площадью пластин
мкГн присоединена к плоскому конденсатору с площадью пластин 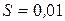 м2 и расстоянием между ними
м2 и расстоянием между ними 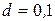 мм. Найти диэлектрическую проницаемость среды, заполняющей пространство между пластинками, если контур настроен на частоту
мм. Найти диэлектрическую проницаемость среды, заполняющей пространство между пластинками, если контур настроен на частоту 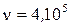 Гц.
Гц.
(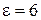 )
)
15.* Уравнение изменения тока со временем в колебательном контуре имеет вид 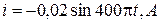 . Индуктивность контура
. Индуктивность контура 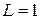 Гн. Найти период колебаний
Гн. Найти период колебаний 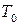 , емкость
, емкость 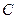 контура, максимальную энергию
контура, максимальную энергию 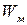 магнитного поля и максимальную энергию
магнитного поля и максимальную энергию  электрического поля.
электрического поля.
(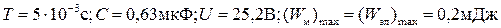 )
)
16.* Найти отношение энергии 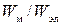 магнитно поля колебательного контура к энергии его электрического поля для момента времени T/8.
магнитно поля колебательного контура к энергии его электрического поля для момента времени T/8.
(W м /W эл=1)
17. Уравнение изменения со временем разности потенциалов на обкладках конденсатора в колебательном контуре имеет вид 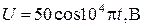 . Емкость конденсатора
. Емкость конденсатора 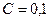 мкФ. Найти период T колебаний, индуктивность L контура, закон изменения со временем t тока
мкФ. Найти период T колебаний, индуктивность L контура, закон изменения со временем t тока 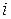 в цепи.
в цепи.
(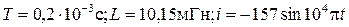 мА)
мА)
18. В момент времени 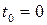 конденсатор идеального электрического колебательного контура заряжают до амплитудного значения
конденсатор идеального электрического колебательного контура заряжают до амплитудного значения 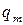 , после чего контур предоставляют самому себе. Найти через какое время
, после чего контур предоставляют самому себе. Найти через какое время 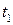 после начала колебаний энергия
после начала колебаний энергия 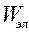 электрического поля конденсатора уменьшится на
электрического поля конденсатора уменьшится на 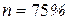 , если период колебаний в контуре
, если период колебаний в контуре 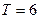 мкс. Какую долю
мкс. Какую долю 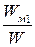 от полной энергии составит энергия магнитного поля в момент времени
от полной энергии составит энергия магнитного поля в момент времени 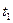 ?
?
(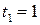 мкс,
мкс, 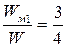 )
)
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 4312; Нарушение авторских прав?; Мы поможем в написании вашей работы!