Общее и каноническое уравнение поверхностей второго порядка

Поверхности второго порядка

Общее уравнение поверхностей второго порядка (т.е. уравнение второго порядка от трех переменных) имеет вид:

(47.1)

С условием 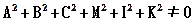(47.2)

справедлива следующая доказанная в параграфе 53 теорема: существует такой ортонормированный базис, в записи которогоуравнение (47.1) имеет вид

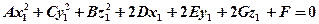(47.3)

с условием (47.4)

Считаем, что если какая-то переменная отсутствует, то это Z, в противном случае делаем соответствующую замену переменных (или B=G=0), и тогда равенство(47.3) с условием (47.4) станет уравнением (35.13) с условием (35.14) (см. §35). Тогда из §35 получим, что уравнение (35.13) и следовательно, уравнение (47.3) при отсутствии хотя бы одной переменной можно привести к одному из следующих:

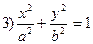(33.4) 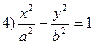(34.1)

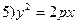(34.3) 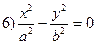(35.21)

(35.30) 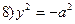(35.32)

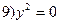(35.31) 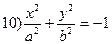(35.23)

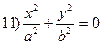(35.20)

Далее положим, что все три переменные в (47.3) присутствуют. Тогда возможны следующие случаи:

I.

II. B=0

III. ,

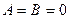
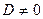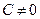
Рассмотрим поочередно все эти случаи:

1.

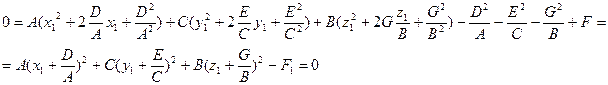
Здесь мы выделим полный квадрат, где

Обозначим за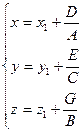

Тогда уравнение (47.3) примет вид:

(47.5).

Исследуем уравнение (47.5).Уравнение (47.5) будем исследовать в зависимости от знаков коэффициентов при 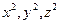. При этом обратим внимание на следующее:

Замечание: не ограничивая общности, всегда можно считать, что пр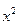и и 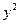стоят коэффициенты одного знака.(ибо из трёх чисел А,В и С хотя бы два из них имеют один и тот же знак и в случае необходимости, можно считать, что один знак имеют числа А и B).

Мы вводим такие числа a, b и с(по условию

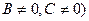
Сначала рассмотрим случай 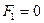. Тогда уравнение (47.5) принимает вид:

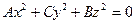(47.6)

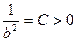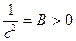; Тогда уравнение (47.6) примет вид

(47.7)

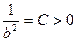; ; В этом случае из уравнения (47.6) получим

(47.8)

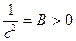Этот случай сводится к предыдущему путём замены знаков обеих частей уравнения (47.6)

4) ; -; Этот случай сводится к первому заменой знаков в обеих частях уравнения (47.6)

Пусть теперь . Тогда, поделив обе части уравнения (47.5) на 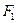получим 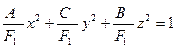(47.16)

Исследуем далее знаки при 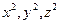в уравнении (47.16). При этом (см. вышестоящее замечание), не ограничивая общности, всегда можно считать, что при стоят коэффициенты одного знака. Попутно, мы также определяем величины a, b, c

1) ; ; ;

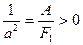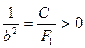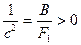В этом случае уравнение (47.16) принимает вид 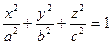(47.17)

2); ; ;

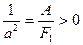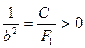Тогда уравнение (47.16) принимает вид 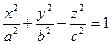(47.18)

3) ; ; ;

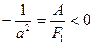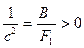Тогда равенство (47.16) принимает вид (47.19)

Или, поменяв знаки в обеих частях уравнения (47.19), получим

(47.20)

4) ; ; ;

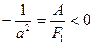Тогда уравнение (47.16) принимает вид 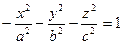(47.21)

или, поменяв знаки в обеих частях уравнения (47.21), получаем

(47.22)

II; ; 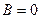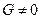в равенстве (47.3), тогда уравнение (47.3) принимает вид

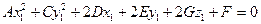
Преобразуем последнее равенство, выделяя при x и y полные квадраты

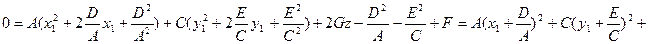
Обозначим далее

Из последнего равенства получаем: , или . Поделив обе части последнего равенства на -2G, получим

(47.23)

Исследуем далее знаки при в равенстве (47.23) При этом если знаки разные, то, поменяв, в случае необходимости, переменные x и y местами, считаем, что коэффициент при 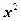положительный. Мы вводим так же величины a и b.

1)

Тогда уравнение (47.23) принимает вид:

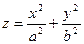(47.24)

2)

В этом случае уравнение (47.23) примет вид:

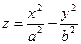(47.25)

3)

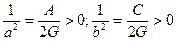
При таких условиях уравнение (47.23) выглядит следующим образом:

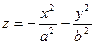(47.26)

Положив далее 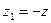, из уравнения (47.26) получим . Поменяв далее знаки в последнем равенстве, из него мы получим уравнение (47.24)

III.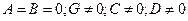

Тогда уравнение (47.3) принимает вид:

(47.27)

В уравнении (47.27) при “y” выделим полный квадрат

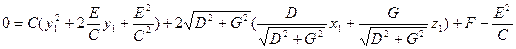(47.28)

Введем новые переменные

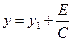
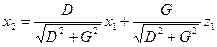
(Согласно §48(и §35)), последнее преобразование является поворотом осей координат и на угол 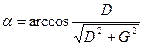по часовой стрелке

Тогда в новой системе координат уравнение (47.28) принимает вид:

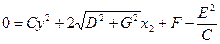, или

(47.29)

Обозначив величину за p введем новые переменные.

Тогда равенство (47.29) в новой системе координат примет вид

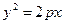(34.3)

(т.е случай III привел нас к уравнению (34.3) и ничего нового не дал).

Дата добавления: 2014-01-04