Комплексные евклидовы пространства

Если два элемента (вектора) некоторого ЕП заданы комплексными координатами (например: 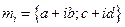), то они находятся в комплексном ЕП.

При этом в комплексном ЕП свойство 1) заменяется на:

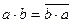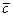(- число, комплексно сопряженное к с)

а свойства 2), 3) и 4) скалярного произведения остаются без изменения.

При этом: (49.6)

В самом деле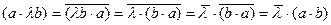, и (49.6) доказано.

Надо иметь в виду, что:

Замечание 1: 4 свойства действительного ЕП в комплексном ЕП не могут иметь места, ибо они противоречат друг другу, так как , что не соответствует свойству 4. (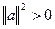при любом a≠0)

Поэтому свойство 1) для комплексных ЕП слегка изменится, а остальные останутся в силе

Замечание 2: Невозможно также определить угол между элементами комплексного ЕП, ибо величина , вообще говоря, будет комплексной и может не быть косинусом некоторого вещественного угла.

В качестве примера советуем показать читателю, что есл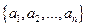и и 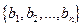- координаты соответственно векторов a и b по базису 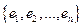, то тогда 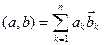- является скалярным произведением (и, следовательно, конечномерное линейное комплексное пространство становится евклидовым), а 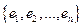будет ортонормированным базисом относительно заданного скалярного произведения.

Дата добавления: 2014-01-04