Визначення величини випадкової похибки

Під час обробки експериментальних даних обчислюють:

ü середнє арифметичне 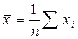; (6.1.)

де n – число вимірювань, х_і – результат окремого вимірювання;

ü стандартне відхилення:

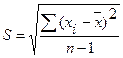(6.2)

Приклад розрахунку стандартного відхилення:

Номер вимірювання	хі		(хі –)^2
	98,10	98,15	0,0025
	98,15	0,0000
	98,22	0,0049
	98,08	0,0049
	98,10	0,0025
	98,24	0,0081
Число вимірювань n = 6	Sхі =588,89	S(хі –)^2=0,0229

ü визначають стандартне відхилення середнього арифметичного:

; (6.3)

Наприклад,

ü визначають ймовірну випадкову похибку:

(6.4)

де t-критерій Стьюдента або ймовірність того, що відхилення окремого вимірювання не перевищує деякої заданої величини, t знаходять за таблицею 6.1.

Таблиця 6.1 – Значення t-критерію при різних значеннях надійності a і

числа визначень n

f = n – 1	a
0.5	0,7	0,9	0,95	0,99	0,999
	1,00 0,82 0,76 0,74 0,73 0,72 0,71 0,71 0,70 0,69	1,96 1,34 1,25 1,19 1,16 1,13 1,12 1,11 1,10 1,09	6,31 2,92 2,35 2,13 2,01 1,94 1,89 1,86 1,83 1,81	12,71 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 2,23	63,66 9,92 5,84 4,60 4,03 3,71 3,50 3,35 3,25 3,17	636,62 31,60 12,94 8,61 6,86 5,60 5,40 5,04 4,78 4,59

Ймовірна випадкова похибка визначає надійний інтервал, на якому перебуває величина, яку слід визначити, х = . Користуючись даними таблиці 6.1, знаходимо, що в наведеному вище прикладі при вірогідності 0,95 істинне значення вимірюваної величини знаходиться у межах:

98,15 ±(0,0276·2,57) = 98,15 ± 0,071.

Часто виникає необхідність порівняти два методи аналізу однієї і тієї ж речовини, щоб встановити який метод більш достовірний. При цьому визначають значимість різних методів, для чого попередньо проводять математичну обробку результатів аналізу за обома методами та знаходять величини середніх арифметичних та 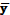, стандартне відхилення середнього арифметичного 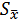та . Потім розраховують експериментальний t-критерій за формулою:

Отриманий t-критерій порівнюють з його табличним значенням при відповідному числі ступенів свободи і ймовірності 0,95. Якщо розраховане значення t-критерію менше табличного, то різниця між методами аналізу незначна і методи адекватні один одному. Якщо t_експ.> t_табл., то методи адекватними визнати неможна.

Приклад розрахунку t-критерію:

При проведенні аналізу речовини двома методами були отримані наступні результати: = 98,1; 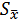= 0,08; n_x = 6; 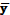= 97,5; = 0,20; n_у = 6.

Визначаємо експериментальне значення t-критерію:

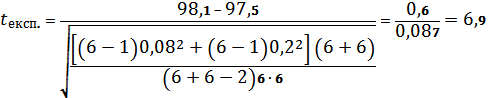
Табличне значення t_0,95 при f = 6+6–2=10 дорівнює 2,23. Оскільки 6,9 > 2,23 та t_експ.> t_табл, то методи неадекватні і значно відрізняються один від одного.

Методами математичної обробки також встановлюють грубі помилки – промахи – результати вимірів, які значно відхиляються від інших. Промахи визначають, використовуючи Q-критерій (таблиця 6.2). Для обробки за Q-критерієм результати вимірювань розташовують у зростаючий ряд і визначають Q_експ. за формулою:

де – х_пр.– результат, який можна вважати промахом;

х_a – результат, найближчий до промаху;

х_мак.та х_мін. – максимальне та мінімальне значення в ряду.

Отримане значення Q_експ. порівнюють з табличним (таблиця 6.2) при даному числі дослідів n. Якщо Q_експ.> Q_табл., то має місце промах. Промахи звичайно відкидають.

Таблиця 6.2 – Значення Q-критерію

Q-критерій	n
Q0,95	0,94	0,77	0,64	0,56	0,51	0,48	0,44	0,42
Q0,99	0,99	0,89	0,86	0,70	0,64	0,58	0,54	0,53

Крім Q-критерію для визначення промахів використовують також 3S-критерій, за яким відхилення одиничного вимірювання від на повинно перевищувати 3S, інакше має місце промах.

Приклад розрахунку Q-критерію:

При аналізі зразку було отримано п’ять результатів: 10,2; 10,3; 10,1; 10,9; 10,3%. За припущенням 10,9% – промах. Розташовуємо результати у порядку зростання: 10,1; 10,2; 10,3; 10,3;10,9. За формулою 6.6 розраховуємо Q_експ.:

Отримане значення Q_експ. порівнюють з Q_табл. Q_табл. при n=5 та ймовірності 0,95 дорівнює 0,64. Оскільки 0,65 > 0,64 і Q_експ.> Q_табл., то має місце промах.

Часто виникає необхідність за 2-3 результатами визначити кількість паралельних аналізів для досягнення необхідної точності.

Приклад визначення необхідної кількості паралельних вимірів:

При аналізі речовини отримані результати 15,6 та 15.0%. Необхідно розрахувати кількість паралельних аналізів для отримання похибки не більше 5%, що забезпечує необхідну точність аналізу. Визначаємо величину випадкової похибки результату аналізу для двох значень (n=2; f = 2 – 1 = 1):

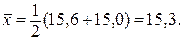
Відхилення дорівнюють 15,6 –15,3 = 0,3 та 15,0 – 15,3 = -0,3;

Визначаємо ймовірну випадкову похибку (при a=0,95; f=1):

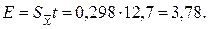
Е можна представити у відсотках: Е,% = Е×100%/ = 3,78×100%/15,3=24,7%.

Для досягнення інтервалу довіри у 5% необхідно змінити t-критерій, який задається числом ступенів свободи f. Оскільки отриманий результат 24,7% приблизно у 5 разів перевищує необхідні 5%, то потрібна величина t-критерію повинна дорівнювати або бути менша наступного табличного значення: t_табл.= 12,7/5=2,54. За таблицею 6.1 визначаємо, що найближчий t-критерій має значення t_0,95 = 2,45 при f=6. Значить, необхідне число паралельних аналізів можна знайти з f = n–1, звідки n = f+1=6+1=7. У цьому випадку:

або у відсотках:

Е,% = Е×100%/ = 0,73×100%/15,3=4,77%.

Дата добавления: 2014-01-04