Интегральное преобразование Фурье

На практике часто используется непериодические сигналы, по этому обобщим ряд Фурье на случай непериодического сигнала и рассмотрим сигнал X_p(t), который представляет собой периодического последовательность импульсов X(t), следующих с периодом T.

X_p(t) =.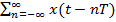

Функция X(t) описывает один импульс, коэффициенты ряда Фурье на интервале [-T/2;T/2] равны:

Сk = * 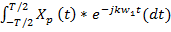(3)

Учитывая, что сигнал на данном интервале может быть представлен одним импульсомX(t), тогда за пределами указанного интервала X(t) = 0 и тогда уравнение (3) может быть записано ввиде:

Сk = * (4)

Из уравнения (4) следует при T=const, коэффициенты C_k зависят только от интервала и тогда:

X(k,w₁)= (5)

Комплексная функция частоты X(k,ω₁)– спектральная характеристика единичного импульса.

Из уравнения (4) и (5) можно записать следующее:

C_k= ;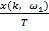

Пределы интегрирования в уравнении (5) являются бесконечными, что следует понимать как разложение в ряд одноименного импульса на интервале [ -∞;+∞ ]и тогда сигнал X(t) можно записать следующим образом, считая, что Tà∞:

X(t) = ;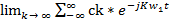

Так как T = 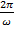, то

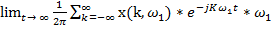X(t) = (6)

Так как при Tà∞, частота первой гармоники ω₁ = 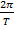она становится бесконечно малой величиной

Приращение частоты ω₁при переходе к соседней гармонике соответствует дифференциалу ω. Под знаком ∑ в уравнение (6) частотные гармоники принимают дискретные значения, то, как Tà∞, то частоты гармоник становятся бесконечно близкими.

Введём обозначение W = k*ω_1.

В этом случае в выражении (6) операция суммирования переходит в операцию интегрирования и тогда (5) и (6) имею следующий вид:

X(ω) = 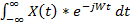(7)

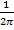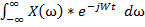X(t) = * (8)

Формулы (7) и (8) представляют собой непериодический сигнал X(t) на интервале [ -∞;+∞ ]. Соответственно в частотной и временной областях данной формулы называется (7) – прямое и (8) – обратное преобразование Фурье.

Функции X(ω) характеризуют спектральный состав сигнала X(t) и называются спектральной плоскостью сигнала X(t), то есть, если с помощью ряда Фурье можно разложить периодические сигналы на бесконечное число гармоник с частотами, принимающими дискретное значение. То интегральное преобразование Фурье позволяет получить непериодический сигнал в виде бесконечного числа гармоник, частоты которых бесконечно близки.

Дата добавления: 2014-01-04