Преобразование Лапласа

Понятие непрерывности систем.

Импульсная и частотная характеристики системы.

Непрерывные системы.

Входные и выходные системные сигналы запишем в следующем виде:

X(t) = {x1(t), x2(t), …, xn(t)} (9)

Y(t) = {y1(t), y2(t), …, yn(t)} (10)

Записанные системные сигналы представляют собой скалярные функции системы, причём система является многомерной, т.к. n входов и m выходов.

Если входные и выходные сигналы системы, а также состояние системы определены в каждый момент времени t и время непрерывно, то такая система тоже является непрерывной.

Если сигнал и состояние системы определяется в дискретный момент времени, то система дискретная.

Связь между X(t), Y(t) задаётся посредством системного оператора, выполняющего преобразование входного сигнала в выходной.

Y (t) = O{X (t)} (11)

Система называется стационарной, если её реакция не зависит от момента подачи входного сигнала, то есть Y(t±t₀) = O{X(t+t₀)}.

Система называется линейной, если оператор системы таков, что выполняется принцип суперпозиции.

O{X₁(t) +X₂(t)} = O{X₁(t)} + O{X₂(t)};

O{α * X(t)} = α * X(t),

α – произвольное число;

Для линейно системы реакция на сумму сигналов X₁(t) и X₂(t) = сумме реакций на каждый из сигналов. Особенностью линейной системы является, то, что благодаря принципу суперпозиции легко определяется выходной сигнал по заданному входному сигналу.

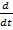àp – это оператор Лапласа. Тогда функция любого порядка записывается в виде:

D= a_mp^m +a_m-1p^m-1 +…+ap) Y(p) = (b_npⁿ+b_n-1p^n-1+…+b₁p)X(p)

= W(p) – передаточная функция;

a_mp^m+a_m-1p^{m -1}+…+a₁p) Y(p)=0 àN(p) (12)

(b_npⁿ+b_n-1p^n-1+…+b₁p) X(p)=0 à M(p) (13)

Корни уравнения (12) и (13) называются соответственно полюсами и нолями функции.

Устойчивой система называется такая, которая способна возвращаться в исходное состояние после выхода из него в результате какого-либо воздействия.

Устойчивой является линейная система, у которой все полюса передаточной функции имеют отрицательные действительные числа, а нули передаточной функции могут иметь как отрицательные, так и положительные числа.

Дата добавления: 2014-01-04