Лекция 9. При помощи производящей функции можно находить моменты ДСВ с целыми неотрицательными значениями

§ Производящая функция

При помощи производящей функции можно находить моменты ДСВ с целыми неотрицательными значениями.

Производящая функция для дискретного распределения, определяемого формулой 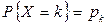, где k = 0,1,2…, называется сумма степенного ряда вида: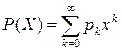

Коэффициентами которого являются вероятности данного закона распределения.

Х				К
р	Р0	Р1	Р2	рк

Дискретное распределение.

Коэффициенты: р₀ + р₁х + р₂х² +…+…

Пусть х = 1. 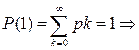По теореме Абеля ряд сходится в точке х = 1 и при том абсолютно для всех х, удовлетворяющих неравенству . Продифференцируем ряд почленно:

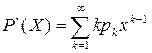
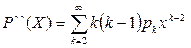Вычислим при Х=1:

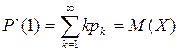- это есть математическое ожидание или α₁

Тогда

§ Биномиальное распределение для ДСВ

Биномиальный закон распределения ДСВ:

В(n, p), где n и p – параметры этого закона

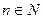– натуральное число,

ДСВ Х, принимающее конечное число целых неотрицательных значений распределена по биномиальному закону, если вероятность того, что СВ Х в n испытаниях появится ровно m раз вычисляется по формуле Бернулли:

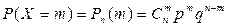, где m = 0, 1, 2,…, n

Х – СВ – число появления события А (успеха) с вероятностью p в схеме Бернулли в n независимых испытаний.

Биномиальный закон распределяется применяется когда СВ:

Х – число выпадения герба при n бросаниях и p = 1/2

Х – число вышедших из строя приборов в n испытаниях

Х – число попаданий в цель при n независимых выстрелов.

Построим производящую функцию для биномиального закона:

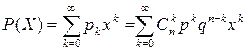Сгруппируем х и р: - бином Ньютона для двух слагаемых.

Найдем математическое ожидание и дисперсию:

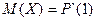
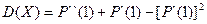
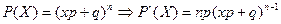
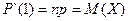
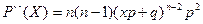
Пример 1: В боевой операции участвуют 50 самолётов; вероятность того, что самолет будет сбит р=0,06. Найти математическое ожидание и σ (X) числа сбитых самолётов. СВ Х – число сбитых самолетов, распределена по биномиальному закону, значит ,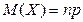

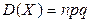
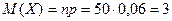
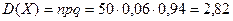
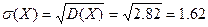
Построим график вероятности и функции распределения: n = 10 p = 0,25

- функция распределения

§ Закон распределения Пуассона

П(λ) предельное распределение для В (n, p)

λ – параметр распределения, λ > 0

ДСВ Х распределена по закону Пуассона с параметром λ если вероятность того, что СВ X примет значение m находится по формуле: , где m = 0, 1, 2, 3…

Применяется если:

X – число атомов радиоактивного вещества, распавшихся за время Т;

Х – число заявок, поступивших за время Т в систему массового обслуживания;

Х – число опечаток в большом тексте.

Предполагается, что среднее значение СВ Х 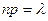за время Т известно.

Составим производящую функцию для закона Пуассона:

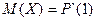
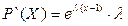
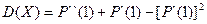
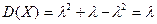
Для закона Пуассона

Дата добавления: 2014-01-04