Залежність ставлення до умов праці на підприємстві від статі

Стать	Ставлення до умов праці на підприємстві
Цілком задово-лений	Скоріше задоволений	Скоріше незадово-лений	Зовсім незадово-лений	Не знаю
чол.
жін.				б
Разом

При цьому можна порівнювати два рядки таблиці, тобто два розподіли, перевіряючи гіпотезу про однорідність: чи однакові жінки та чоловіки у своєму ставленні до умов праці на нашому підприємстві (див. табл. 5.3)? Але можна поставити питання й інакше: чи не має зв'язку між статтю та ставленням до умов праці?

Тим самим ми переходимо до гіпотези про незалежність. Дійсно, якщо відношення до умов праці чоловіків і жінок істотно відрізняються, то можна вести мову про істотний статистичний зв'язок між ознаками «стать — ставлення до умов праці». Так само і у випадку розподілу студентів за кольором волосся та очей (див. табл. 2.3). Там ми маємо 3 ряди розподілу за кольором волосся або 3 ряди за кольором очей. Якщо розподіл за кольором волосся людей із блакитними очима істотно відрізняється від розподілу за тією ж ознакою, але вже сірооких, а тих — від карооких, то між цими ознаками існує статистичний зв'язок.

Таким чином, критерій може бути використаний для доказу наявності істотного зв'язку. Застосовуючи КРА, ми також визначали форму (напрям) та тісноту. В даному випадку, коли ознаки якісні, вести мову про форму зв'язку мабуть не має сенсу, щодо напрямку, то його іноді можна визначити візуально за таблицею співзалежності (ТС): між кольором очей та волоссям (або навпаки) зв'язок прямий. Для визначення тісноти зв'язку використовують коефіцієнти співзалежності.

Наприклад, для неквадратних таблиць коефіцієнт Чупрова має вигляд [9]:

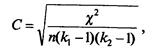
де K₁ K₂- число рядків та стовпчиків таблиці. Коефіцієнт Крамера обчислюють за формулою

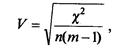
де т = тіп(k ₁ k₂ ) п - число елементів сукупності.

У наведених формулах використовується критерій Пірсона X², який має вигляд:

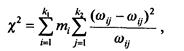
де i — номер підгрупи за першою ознакою;

k_i- число груп за першою ознакою;

k_j- число груп за другою ознакою;

w_ij — частість підгрупи i у групі j;

w_j- частість групи j у всій сукупності;

m_i — число одиниць у групі i. У випадку незалежності ознак w_ij = w_j i x² = 0. Ці коефіцієнти приймають значення від 0, при відсутності зв'язку, до 1, при функціональному зв'язку.

У практиці статистичних досліджень нерідко необхідно аналізувати альтернативні розподіли, коли су­купність розподіляється за кожною ознакою на дві групи з протилежними характеристиками. Наприклад, можна аналізувати успішність студентів залежно від статі [9], виділивши дві групи: студенти, що здали іспити, та студенти, що не здали іспити (табл. 5.4).

Приклад 5.3Таблиця 5.4 Залежність успішності студентів від статі

Стать	Кількість студентів	Разом
здали	Не здали
Жінки	a=25	Ь=2	а + Ь = 27
Чоловіки	с=20	d=3	с+d=23
Разом	а + с = 45	Ь+d=5 +(1=5

Тісноту зв'язку у даному випадку можна розрахувати за допомогою коефіцієнта асоціації:

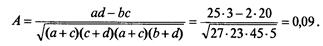
Тобто між статтю та успішністю студентів зв'язок надто незначний, практично він відсутній. Отриманий висновок неодмінно справедливий тому, що істотними факторами успішності є не стать, а відвідування лекційних та практичних занять, кількість годин самостійної роботи і т. п.

Використання таблиць співзалежності дуже поши­рене при вивченні взаємозв'язку ознак різної природи:

в економіці, соціології, біології, медицині. В порівнянні з КРА їхній вибір легше аргументувати, додержати необхідні умови застосування, а отримані ре­зультати інтерпретувати. Ми вже згадували про про­блему вибору факторів у КРА, крім того, на практиці не завжди забезпечується виконання відповідних постулатів (взаємозв'язок факторів, нормальність розподілу, відповідність шкал та ін.).

Прагнення подолати подібні перешкоди іноді приводить деяких дослідників до віртуозних математичних трюків, аби тільки «притягнути за вуха» наукові методи. Щоб глибоко зрозуміти і оволодіти досягненнями світової статистичної науки, особливо останніх десятиріч, потрібна відповідна підготовка. Ми вважаємо, що спеціалісту з економіки та управління при вирішенні своїх прикладних задач за допомогою пакетів статистичних програм перш за все необхідно чітко уявити, який статистичний інструмент у яких випадках застосовувати, вміти інтерпретувати отримані результати. Саме тому ми настійно рекомендуємо при вирішенні конкретної задачі, поки не буде набуто певного досвіду, користуватись прикладами з авторитетних літературних джерел. Це дасть змогу:

а) визначити, який метод застосовується в задачі, подібній до вашої;

б) обчисливши контрольний приклад наявними у вас засобами (статистичними програмами), порівняти

значення результатів, їхню інтерпретацію та термінологію.

У цьому плані із наведеного списку ми насамперед рекомендуємо [1—5, 16, 17].

Звичайно, параметричні та непараметричні методи не є взаємозамінюваними. Але в деяких випадках для зручності замість перших можна застосовувати інші, замінюючи метричні шкали, наприклад, порядковими. Але треба пам'ятати, що менша глибина аналізу, яка буде досягнута при цьому, може бути виправдана ли­ше більшою його аргументованістю, надійністю. Нагадаємо, що за допомогою непараметричних методів можна лише визначити тісноту зв'язку та його істотність, КРА дає змогу до того ж вивчити і його форму.

Широко відомі міри взаємозв'язку, які не базуються на статистиці x² Для випадків, коли ТС побудо­вана для ознак, одна з яких або обидві виміряні за до­помогою порядкової шкали, наприклад «колір очей — колір волосся», переважно застосовуються так звані методи рангової кореляції: міри Кендала;

Стьюарта та Спірмена. Якщо ознаки в ТС тільки дискретні («стать», «спеціальність», але не «вік»), то рекомендуються міри Гудмена-Крускала. І, нарешті, існує група методів спеціально для ТС розміром 2х2 [І].

Популярний приклад: «Курять — не курять; хворіють — не хворіють». Очевидна умовність такого поділу. Що значить «хворіють»? Як часто? Якими саме захворюваннями? А що означає «не курить»? Зовсім чи не зовсім? Взагалі, однозначні відповіді не завжди коректні.

Дійсно, є суто альтернативні ознаки, наприклад «стать» (принаймні, так прийнято вважати). Але, якщо є змога, дозволяє обсяг сукупності, треба намагатись «розтягнути» шкалу вимірювання. Наприклад, якщо ви формулюєте питання анкети для соціологічного опитування робітників підприємства, то для запитання «Чи задоволені Ви умовами праці?» слід підказувати такі варіанти відповіді: не задоволений, скоріше неза-доволений, ніж задоволений; важко відповісти; скоріше задоволений, ніж незадоволений; задоволений. Якщо ви запропонуєте тільки два варіанти відповіді і тим самим змусите людину відповісти тільки «задоволений» або «незадоволений», то ви не вловите відтінки в настрої людей. Але слід мати на увазі, що іноді корисно зробити і навпаки.

Так, згідно з теорією слід уникати застосування критерію x² в тих випадках, коли значення окремих клітинок ТС менше 5. При бажанні можна знайти в літературі рекомендації, як знайти вихід з цього положення. В літературі та розпечатках статистичних па­кетів вони пов'язані з іменами таких авторів, як Ієтс (Yates), Кохрен (Сосhгаn), Мантель (Маntеl). Але їх застосування потребує певної обережності. У таких випадках іноді краще провести об'єднання рядків чи стовпчиків ТС. Зрозуміло, що це можна зробити по відношенню, наприклад, до ознаки «задоволеність умовами праці» або «колір волосся», а не ознаки «спеціальність».

Вважається, що глибокий статистичний аналіз включає не тільки перевірку гіпотези про незалежність, а й порівняння самих критеріїв для більш повного розуміння результатів.

6. Вимірювання тісноти зв'язку за допомогою кореляційного і дисперсійного аналізу супроводжується певними складностями і вимагає громіздких обчислень. Для орієнтовної оцінки тісноти зв'язку користуються наближеними показниками, які не вимагають трудомістких обчислень. До них потрібно віднести:

коефіцієнт кореляції знаків Фехнера, коефіцієнт кореляції рангів Спірмена і Кендала.

Коефіцієнт кореляції знаків Фехнера визначають на співставленні знаків відхилень від середньої і на підрахунку числа співпадань і неспівпадань знаків.

Коефіцієнт кореляції знаків визначають за формулою

і=. (и-у)/(и+у)

де u — число пар с однаковими знаками відхилень х і у від х і у; v — число пар с різними знаками відхилень

х і у від х і у. Коефіцієнт кореляції знаків коливається в межах від —1 до +1. Чим ближче до 1, тим сильніший зв'язок. Знак + або — вказує напрям зв'язку. Якщо u = v, то i = 0 і зв'язку немає.

Приклад 5.4 [18

Таблиця 5.5

Вартість основних фондів (ОФ) та випуск продукції (млн. грош. од.)

№ Підпри­ємства	Вартість ОФ (x)	Випуск про-дукції (у)	Знак відхилення
х-х	У-У
		2,4	-	-
		4,0	—	—
		3,6	-	—
		4,0	-	—
		4,5	-	-
		4,6	+	—
		5,6	+	+
		6,5	+	+
		7,0	+	+
		5,0	+	+
Разом		47,2	X	х

х = 108/10 = 10,8 млн. грош. од.,

у = 47,2/10 = 4,72 млн. грош. од.

Таким чином, u = 9, v = 1. Тоді

I=(9-1)/(9+1)= 0,8

Це означає, що зв'язок між вартістю основних фондів та випуском продукції прямий та досить тісний.

Розглянемо ще один метод оцінки тісноти зв'язку на основі розрахунку коефіцієнта кореляції рангів. Його основна відмінність полягає в тому, що він обчислюється не на основі первинних даних, а на основі рангів, які присвоюються всім значенням досліджуваних ознак, що розміщені у порядку зростання. Якщо значення співпадають, то ранг визначається шляхом ділення суми рангів на число значень.

Коефіцієнт кореляції рангів Спірмена визначається за формулою

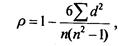
де d² - квадрат різниці рангів для кожної одиниці d = х — у, п — обсяг сукупності.

Коефіцієнт кореляції рангів Спірмена також коливається від —1 до +1. Чим ближче до 1, тим тісніший зв'язок. Знак + або — вказує напрям зв'язку. Якщо ранги за обома ознаками співпадають, то зв'язок прямий. Якщо p=0, то зв'язок між ознаками відсутній. Обчислимо коефіцієнт кореляції рангів за даними по­переднього прикладу (табл. 5.6).

Таблиця 5.6 Розрахунок коефіцієнта кореляції рангів Спірмена

Ранги	Ранги по х	Ранги по у	Різниця рангів	d^2
			0	0
		3.5	-1.5	2,25 &.&^
			+1
	4.5	3.5	+1
	4.5		-0.5	0.25
			-1
			-1
			-1
			+3
Разом	X	X	X	16.5

Ранги вартості основних фондів для четвертого та п'ятого підприємств визначалися як середня арифме­тична з х = (4+5)/2 = 4,5. Аналогічно для другого і четвертого за випуском продукції. Підставивши у формулу, отримаємо:

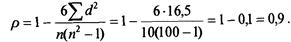
Коефіцієнт кореляції свідчить, що зв'язок між вартістю основних фондів та випуском продукції прямий та тісний.

Ранговий коефіцієнт кореляції більш точний порівняно з коефіцієнтом кореляції знаків, тому що він враховує не тільки знаки відхилень, а й місце величини ознаки в даному ряду.

[1] Ми не говоримо просто цифри (25, 45, 6 000 000) як в математиці, а, наприклад, 50,4 млн. населення.

[2] Скільки тон перевезено на 1 кілометр.

[3] Адитивність –підсумок.

[4] Отже, в принципі темп зростання схожий на коефіцієнт, різниця лише в тому, що темп зростання виражений в процентах (хоча можна і так, як і k).

[5] Відносні величини інтенсивності виражаються переважно в промілях.

[6] Якби ми за найвищий ранг ми взяли незадоволення, то отриманий відсоток свідчив би про негативне ставлення.

[7]

[8] Різниця між темпом і коефіцієнтом в тому, що коефіцієнт виражається лише в частках, а темп – частіше в відсотках (хоча може вимірюватися і в частках).

[9] Для цього необхідно, щоб останній показник першого ряду і перший показник другого ряду мали однакові рівні (наприклад, один період часу).

[10] Базове значення.

[11] Виявлення впливу факторів на динаміку чи відносне відхилення параметрів отримав назву "факторного аналізу".

[12] Ціна, що встановлюється при видобутку нафти чи газу.

[13] Тобто розглядається в зміні, динаміці, часі.

Дата добавления: 2014-01-04