Обоснование выбора методов оптимизации

.

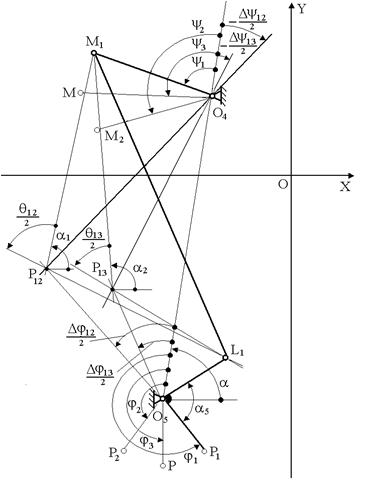
Варьируемыми параметрами являются длина звена, координаты неподвижной шарнирной точки и углы и. При заданном векторе остальные параметры (длины звеньев и, и угол) определяются путем проектирования механизма по трем положениям ведомого и ведущего звеньев. Этим обеспечивается близкая к линейной зависимость длины стежка от положения рычага регулятора. Алгоритм синтеза механизма по трем положениям ведомого и ведущего звеньев приведен ниже. Обозначения в алгоритме приведены в соответствии с рисунком 9. Интервалы углов поворота ведущего и ведомого звеньев определяются со своими знаками как

Через точк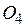и и 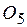проводятся лучи под углами -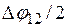, -,-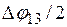, -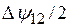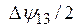к прямой 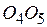. При отрицательных значениях этих углов лучи поворачиваются относительно прямой 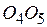по часовой стрелке, при положительных – против движения часовой стрелки.

На каждом шаге оптимизации необходимо определять максимальное значение переменного момента 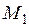. С целью уменьшения времени счета при оптимизации максимальные значения момента 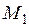вычислялись по 5 положениям коромысла , после чего зависимость 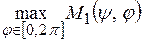аппроксимировалась кубическим сплайном 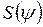[6].

При проектировании механизма необходимо удовлетворить только габаритным ограничениям

В такой постановке задача проектирования механизма регулятора длины стежка решена для механизма подачи материала с длиной стежка до 5 мм. В результате проектирования удалось уменьшить значение момента в 2,6 раза по сравнению с исходным механизмом, который был получен при синтезе механизма только по положениям звеньев, и применялся в швейной машине 1022М класса.

Алгоритм синтеза механизма регулятора длины стежка по трем заданным положениям ведущего и ведомого звеньев:

1. ;

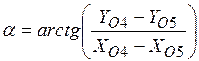2. ;

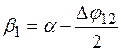3. ;

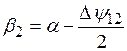4. ;

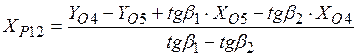5. ;

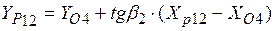6. ;

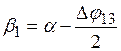7. ;

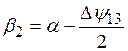8. ;

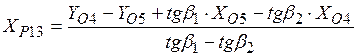9. ;

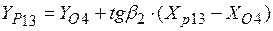10. ;

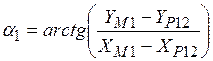11. ;

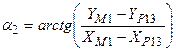12. ;

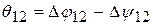13. ;

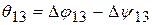14. ;

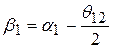15. ;

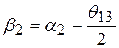16. ;

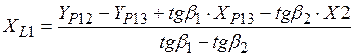17. ;

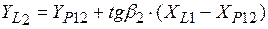18. ;

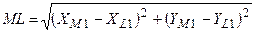19. ;

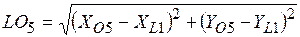20. ;

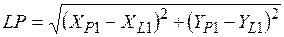21. .

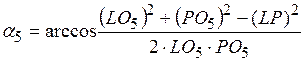2.2 Оптимального проектирования механизмов ультразвуковой

швейной машины

Ультразвуковая швейная машина предназначена для соединения материалов, содержащих синтетические волокна, при помощи ультразвуковых колебаний и содержит два основных механизма: механизм пуансона и реечный механизм подачи материалов. Механизм пуансона прижимает соединяемые материалы к акустическому узлу, который получает питание от ультразвукового генератора.

Рабочий цикл ультразвуковой швейной машины состоит из двух основных этапов: перемещения материала и сварки. Так как заданная продолжительность процесса сварки обеспечивается выстоем пуансона в нижнем рабочем положении, то цикловая производительность машины будет тем выше, чем большую часть цикла будет занимать высота пуансона. В то же время цикловая производительность машины зависит от величины перемещения материала (длины стежка). Таким образом, фазовый угол поворота главного вала машины, соответствующий выстою пуансона, лимитируется временем перемещения материала. Поэтому задача выбора оптимальных параметров механизмов должна решаться при их совместном проектировании.

К механизмам пуансона предъявляются следующие технологические требования: колебания пуансона на выстое при выполнении процесса сварки не должны превышать 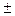0,02 мм, ход пуансона должен быть не менее 6 мм, сварочное усилие должно регулироваться в пределах 20 – 100 Н, время сварки должно быть не менее 0,02 секунды. Кроме технологических требований необходимо удовлетворить габаритным ограничениям, вытекающим из необходимости установки механизма в головку существующей швейной машины, в частности, в головку швейной машины 1022 класса Оршанского завода «Легмаш», и обеспечить хорошие динамические характеристики.

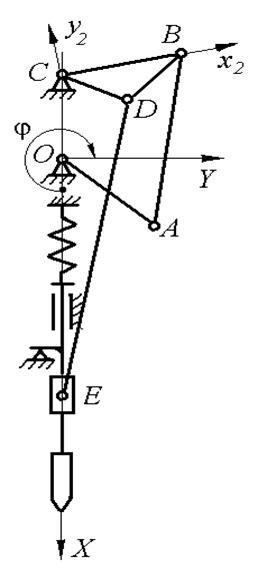
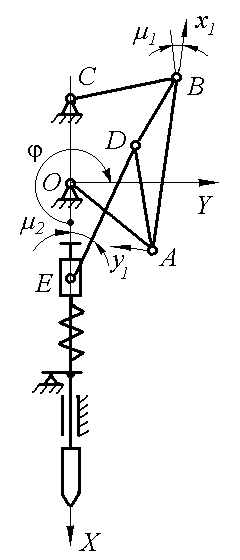
Для оптимизации была принята существующая структурная схема механизма подачи пуансона [10] (рисунок 10). Она состоит из ведущего звена ОА, присоединенной к нему двухповодковой группы ABC с тремя вращательными кинематическими парами, образующей с ведущим звеном шарнирный четырехзвенник ОАВС, и двухповодковой группы DE с внешней поступательной парой, состоящей из шатуна DЕ и ползуна Е. B зависимости от того, к какому звену присоединяется точка D шатуна DE (к коромыслу BС или шатуну АB шарнирного четырехзвенника), получаются две группы механизмов. Ведомое звено ВС шарнирного четырехзвенника может быть коромыслом или кривошипом.

С помощью рычажных механизмов невозможно осуществить точный выстой пуансона на большом интервале угла поворота ведущего звена. поэтому в конструкции механизма предусмотрено кинематическое размыкание звеньев. Предполагается, что во время этого размыкания, пуансон неподвижен, т.е. находится на упоре, и обеспечены необходимые условия сварки. Однако за счет упругой податливости обрабатываемого материала, упора и самого пуансона при некоторых режимах работы может происходить отскок пуансона от обрабатываемого материала. Отскок пуансона недопустим, так как он приводит к нарушению режима сварки и увеличению шума и вибрации машины.

Необходимое сварочное усилие создается пружиной. В зависимости от того, каким образом пружина взаимодействует с механизмом: нагружение ползуна осуществляется при его подъеме (рисунок 4.40а) или на выстое (рисунок 4.40б), по разному формулируются ограничения на динамические характеристики механизма.

а) б

а) нагружение ползуна при подъеме пуансона;

б) нагружение ползуна на выстое пуансона.

Рисунок 10 – Кинематические схемы механизмов пуансона

Задачу оптимального проектирования механизма подачи пуансона можно сформулировать следующим образом: подобрать параметры механизма так, чтобы интервал поворота главного вала, соответствующий выстою пуансона, был максимально возможным, а скорость ползуна в начале его выстоя была меньше допустимой, определяемой минимальной скоростью, при которой происходит отскок пуансона. Искомыми являются длины всех звеньев механизма ОА, АВ, ВС, DЕ, координаты точки С (Хс, Ус) в неподвижной системе координат ХОУ, координаты точки D (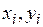) в подвижной системе координат 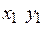, связанной с шатуном АВ, или в подвижной системе координат 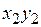, связанной с коромыслом ВС, и координата точки E (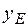), определяющая положение направляющей ползуна. Итого имеется девять варьируемых параметров механизма.

За основной критерий оптимальности принят интервал поворота ведущего звена, соответствующий выстою пуансона. Так как процедуры оптимизации предполагают поиск минимума целевой функции, то за целевую принята функция:

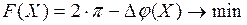, (15)

где 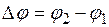; 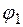, 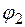- углы поворота ведущего звена ОА, соответствующие началу и концу интервала выстоя пуансона 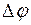(рисунок 11); X - вектор варьируемых параметров ().

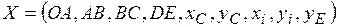На проектирование механизма были наложены следующие ограничения:

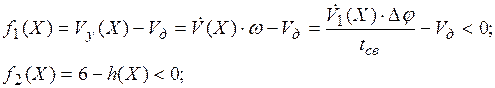
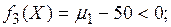
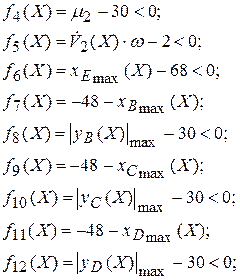(16)

где 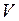– скорость ползуна;

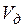- допустимая скорость ползуна;

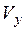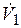, - скорость и аналог скорости ползуна в момент установки пуансона на упор при заданном векторе X;

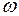- частота вращения ведущего звена;

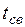- заданное время сварки материалов;

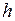- ход пуансона;

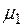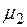, - углы давления;

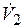- аналог скорости ползуна в конце выстоя пуансона;

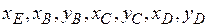- максимальные значения координат соответствующих точек механизма в неподвижной системе координат ХОY.

Первое и второе ограничения на проектирование обусловлены технологическими требованиями. Первое ограничение обеспечивает условия отсутствия отскока пуансона в момент его установки на упор, при котором скорость 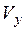должна быть меньше допустимой скорости ползуна 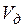. Допустимая скорость ползуна 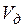, при которой еще не происходит отскока пуансона, вычисляемая по формуле [3], принята равной 0,6 м/с. Скорость ползуна 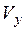в момент установки пуансона на упор определяется аналогом скорости 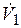и частотой вращения 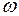ведущего звена. Величина частоты вращения 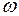определяется через интервал выстоя пуансона 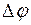и время сварки 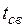, равное 0,02 с. Второе ограничение обеспечивает минимальный ход пуансона, который должен быть не менее 6 мм.

Последующие три ограничения определяют динамические характеристики механизма подачи пуансона. В третьем ограничении угол давления 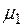не должен превышать 50 градусов либо на интервале подъема пуансона (рисунок 10а), либо во время выстоя пуансона (рисунок 10б), так как в эти периоды движения на ползун действует усилие, создаваемое пружиной, величина которого равна 100 Н. В четвертом ограничении угол давления 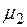не превышает 30 градусов на всем протяжении кинематического цикла. В момент подъема пуансона скорость ползуна может достирать больших значений. Увеличение этой скорости усиливает шум и может нарушить силовое замыкание пуансона на ползун. В пятом ограничении эта скорость не должна превышать 2 м/с. После проектирования проверялось наличие постоянного силового замыкания пуансона на кинематическую цепь по выполнению условия (3.39).Определение величины этой скорости приведено выше.

Остальные ограничения габаритные, обусловлены размещением механизма в головке швейной машины. Максимальные значения координат соответствующих точек механизма определяются на каждом шаге оптимизации.

Углы 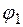и 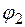соответствуют точкам пересечения прямой 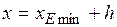c кривой 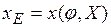(рисунок 11) и определяются на каждом шаге оптимизации. Угол 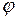, определяющий положение ведущего звена ОА, отсчитывается от оси Х. Вращение ведущего звена осуществляется по часовой стрелке.

Внутри каждой из указанных групп механизмов получено несколько оптимальных в указанном смысле механизмов подачи пуансона. Шарнирный четырехзвенник первого оптимального решения обеих групп механизмов имеет коромысло, а шарнирный четырехзвенник второго оптимального решения представляет собой двухкривошипный мexанизм. Внутри каждого оптимального решения учитывался вариант сборки четырехзвенника ОАВС.

X – координата точки Е, определяющая положение ползуна;

- угол поворота ведущего звена ОА; 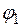, 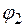- углы поворота ведущего звена ОА, соответствующие началу и концу интервала 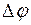выстоя пуансона; Н – ход ползуна; H – ход пуансона;

Рисунок 11 – График перемещения ползуна механизма пуансона.

В ультразвуковой швейной машине для перемещения материала применяется также реечный механизм подачи. Задачей оптимального проектирования реечного механизма подачи материала является определение таких параметров кинематической схемы механизма, при которых заданное максимальное перемещение материала осуществляется за время, отведенное циклограммой машины. Задача оптимального проектирования этого механизма формулируется также как и задача оптимального проектирования механизма подачи материала универсальной швейной машины с большой длиной стежка.

Задача поиска оптимальных параметров механизмов ультразвуковой швейной машины решается в следующей последовательности:

1) сначала определяются параметры механизма пуансона из условия минимизации целевой функции (15) и удовлетворения всем ограничениям на проектирование;

2) затем определяются параметры механизма подачи материала из условия минимизации целевой функции (11) и удовлетворения всем ограничениям на проектирование;

3) проводится анализ полученной циклограммы машины; если требования, предъявляемые к циклограмме машины, удовлетворены, то решение задачи заканчивается или осуществляется переход к следующему пункту;

4) интервал 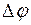выстоя пуансона уменьшается до тех пор, пока не будут удовлетворены требования циклограммы машины при решении задачи пункта 2.

ПРИ ОПТИМАЛЬНОМПРОЕКТИРОВАНИИ МЕХАНИЗМОВ

Выше отмечалось, что задача оптимального проектирования формулируется как задача нелинейного программирования. Точное аналитическое решение задачи нелинейного программирования в большинстве случаев невозможно, так как целевая функция имеет сложную структуру и известен лишь алгоритм ее вычисления при фиксированных параметрах. Поэтому для решения задачи нелинейного программирования применяются поисковые методы оптимизации, обеспечивающие численное решение задачи при помощи ЭВМ.

Существуют различные классификации методов поисковой оптимизации, в которых различают методы поиска безусловного минимума и условного минимума целевой функции. В методах поиска первой группы предполагается, что на вектор искомых параметров 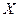не наложено никаких ограничений. В методах второй группы ищется минимум целевой функции 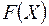внутри допустимой области .

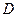В основе методов поиска безусловного минимума лежит итерационная схема

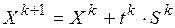, (17)

где 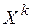- вектор параметров механизма на 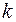-ой итерации; 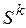- вектор сдвига из точки 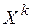в направлении минимума на 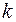-ой итерации; - величина шага вдоль направления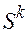

Дата добавления: 2014-01-04