Регулярные и критические невырожденные точки гладких функций

Ниже мы будем рассматривать только гладкие функции.

Рассмотрим, какие особенности присущи функциям. В свое время
П. Монтень тонко заметил, что «функции, как и живые существа, характеризуются своими особенностями». Именно особенности гладких функций позволяют выявить качественные изменения фазовых траекторий на данном фазовом пространстве.

Если задана гладкая функция 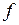, то точка 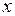называется регулярной (некритической) точкой функции 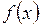, если:

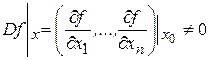. (4.20)

В том случае, если в некоторой точке 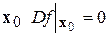, а функция 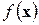имеет смысл потенциальной функции, то эта точка характеризует состояние равновесия (устойчивого или неустойчивого) и ее называют критической. При этом тип равновесия определяется собственными значениями матрицы устойчивости, или матрицы Гессе в точке :

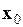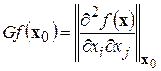. (4.21)

Такого рода точки х ₀, где 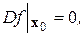и гессиан 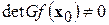, называют критическими вырожденными точками.

Если все критические точки функции 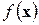являются критическими невырожденными, то функция 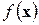называется морсовской.

Всякая невырожденная критическая точка функции f изолирована в множестве всех критических точек этой функции, то есть обладает окрестностью, свободной от других критических точек.

Критические точки имеют большую ценность, чем регулярные (некритические), так как именно они в основном характеризуют глобальные качественные изменения в поведении функции .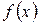

Рассмотрим морсовскую функцию 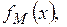, вид которой показан на рисунке 4.5.

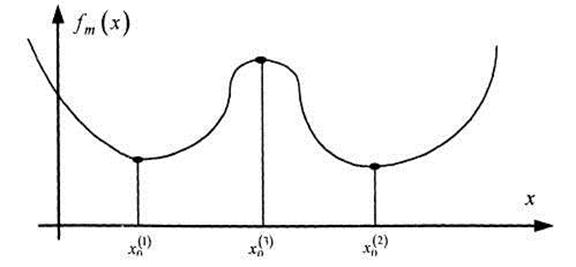
Рисунок 4.5 – Морсовская функция с двумя “бассейнами” (областями притяжения) и аттракторами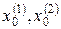

Здесь три критические изолированные точки, причем точки 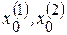имеют по морсовской классификации индекс 0, а 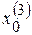– индекс 1.

Точки 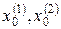являются аттракторами, причем каждый со своим «бассейном» (областью притяжения).

Важность критических точек состоит в том, что при переходе из одного «бассейна» в другой всегда необходимо проходить через критическую точку, имеющую другой морсовский тип.

Следовательно, если 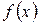имеет лишь изолированные критические точки (является морсовской) и координаты всех этих точек известны, можно определить все качественные изменения в поведении функции 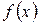при условии, что известен тип каждой морсовской точки.

Немалую роль в поведении некоторых динамических систем играют критические вырожденные точки, наличие которых подчас приводит к внезапному качественному изменению состояния систем. Появление критических вырожденных точек 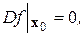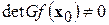обычно связано с погружением данной функции 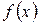в параметрическое семейство функций, т.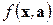е. , где 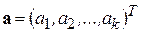– вектор параметров.

Перестройку качественной картины движения динамической системы, анализ особенностей отображения у функции 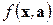при плавном изменении параметров изучают теория бифуркаций, а также теория особенностей гладких отображений. Приложения этих теорий к исследованию скачкообразных реакций механических, физических, химических, биологических, экономических систем, систем управления и иных систем на плавное изменение внешних условий (управляющих параметров) получили название теории катастроф.

Дата добавления: 2014-01-04