Неморсовские функции. Функции катастроф

Критические точки функции 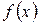, в которых гессиан 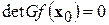, являются неизолированными вырожденными, или неморсовскими критическими точками.

Если функция 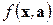зависит от одного или более управляющих параметров 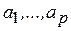, то матрица Гессе 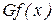и ее собственные значения зависят от этих параметров. В этом случае возможно, что при некоторых значениях управляющих параметров одно (или несколько) собственных значений матрицы G может (могут) обратиться в нуль.

Тогда можно найти такую замену переменных 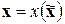, что функция 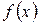может быть представлена в виде суммы двух функций: неморсовской 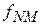, зависящей от координат 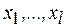, которые являются гладкими функциями переменных 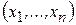и параметров 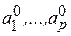, и морсовской 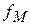, зависящей от 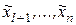, которые являются гладкими функциями только искомых координат 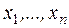, то есть:

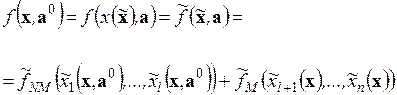. (4.22)

Назовем координаты 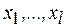неморсовскими, а 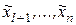, соответственно, морсовскими.

Р. Том показал, что (4.22) может быть представлено в следующем виде:

. (4.23)

Функцию 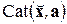называют функцией катастрофы, или просто катастрофой. Из представления (4.23) и названия функций можно сделать зрительный вывод о том, что именно неморсовские функции «создают катастрофы.

Возмущение функции одной переменной в морсовской критической точке не влияет на качественную природу этой функции и, хотя при этом критическая точка сдвигается, тип критической точки остается без изменения (рис. 4.6), то есть морсовские функции структурно (качественно) устойчивы.

Рисунок 4.6 – Возмущение функции в морсовской критической точке

Рассмотрим, что происходит, если возмущение действует в окрестности неморсовской критической точки.

Пусть неморсовская функция одной переменной 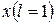представлена выражением:

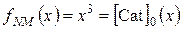, (4.24)

а функция возмущения имеет вид .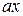

С учетом возмущения запишем:

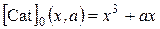. (4.25)

Проанализируем свойства этого 1-параметрического семейства функций F(x;a), приведенного на рисунке 4.7.

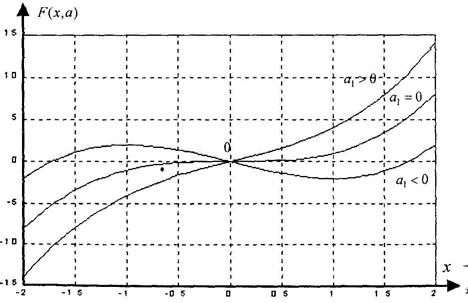
Рисунок 4.7 – Параметрическое семейство функций F(x;a)

Из рисунка видно, что:

1) при 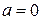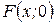имеет критическую вырожденную точку в х_о = 0;

2) при 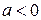имеет в плоскости две изолированные морсовские критические точки;

3) при 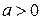F(x;a) не имеет критических точек.

Отсюда можно сделать вывод: возмущение функции f(x) в неморсовской критической точке вызывает качественное изменение в поведении f(x) в окрестности данной критической точки.

Дата добавления: 2014-01-04