Вынужденные колебания простейшей системы

Изобразим движение подвешенной на колесе массы m, когда колесо катится по жесткому пути, имеющему неровности косинусоидальной формы.

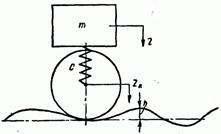
В этой системе силы инерции массы m, т.е. 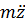, уравновешиваются силами, возникающими при деформации рессоры (z – z_k), т.е. силой ж(z – z_k).

Используя принцип Даламбера

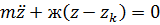
С учетом 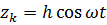проведем преобразование данного уравнения:

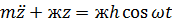
Поделив все члены этого уравнения на m, получим

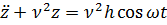
где 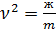– круговая частота свободных колебаний системы.

Общее решение этого уравнения с правой частью (неоднородного) можно представить как сумму решения однородного уравнения z₁ и частного решения неоднородного уравнения z₂, т.е. z=z₁+z₂.

Найдем вначале частное решение уравнения. Допустим

и подставим его в общее уравнение:

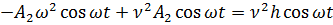
Откуда

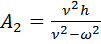т.е. .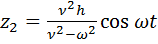

Решение однородного уравнения можно представить в виде:

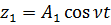
Тогда общее решение уравнения представляется как

.

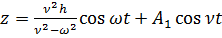Начало отсчета времени (t=0) в этой системе можно принять для такого момента, когда z=0. Подставив, получим

,

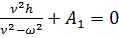Откуда .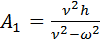

Подставляя А₁ в основное уравнение, получим

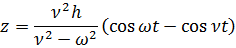
Величину 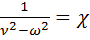называют коэффициентом нарастания колебаний.

Приняв это значение, уравнение запишется

.

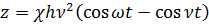Это и будет общим решением нашего уравнения при принятых выше начальных условиях.

Исследуем поведение колебательной системы в том случае, когда частота возмущений 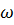приближается к частоте собственных колебаний .

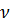Для удобства дальнейшего анализа формулу (1.47) пред­ставим в следующем виде:

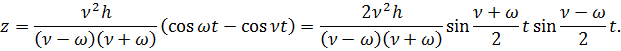
Обозначая 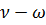= 2ε, подставим это выражение в преды­дущую формулу и, полагая, что 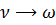, получим

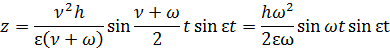
Преобразуем

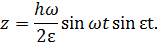
Поскольку ε малая величина, то ее период T₁ весьма велик и значительно больше периода T₂, определяемого частотой возмущений за счет неровностей ω.

Это позволяет рассматривать такие колебания (при близ­ких ω и 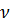), как колебания с частотой ω и с переменной ампли­тудой. Такие колебания называют биением с периодом 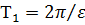. С приближением ω к ν

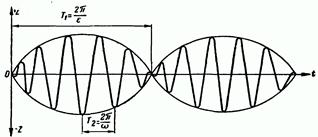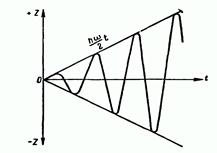
период Т₁ увеличивается. При точном совпадении величин v и ω наступает явление резонанса.

Биение Резонанс

Дата добавления: 2014-01-04