Уравнение колебаний модели плоской двухосной тележки

Используя такую модель можно получить подробную информацию динамических свойств вагона. Появляется возможность учесть, кроме подпрыгивания ещё и колебания галопирования, а также неодновременность задания (запаздывание) возмущения по две колесных пары.

Рисунок.

В модели масса m (тележка) совершает колебания (подпрыгивания) z и галопирование φ_у. Причиной колебаний являются возмущения 𝜂₁(t) и 𝜂₂(t) передаваемые через первую и вторую колесные пары. При движении экипажа с поступательной скоростью υ неровность 𝜂₂ повторяет неровность 𝜂₁ через некоторое время τ, называемым транспортным запаздыванием. Это время определяется скоростью движения υ и расстоянием между осями колесных пар 2am и рассчитывается по формуле:

τ=2am / υ

Выражение для неровностей под первой и второй колесными парами запишется в следующем виде:

𝜂₁(t) = 𝜂(t)

𝜂₂(t) = 𝜂 (1 – τ)

𝜂(t) – единичное возмущение входного воздействия.

Уравнение колебаний подпрыгивания примет следующий вид:

F_ин + F_у1 +F_∂1 + F_у2 + F_∂2 = 0

Перемещение в точках 1 и 2 складываются из колебаний подпрыгивания z и вертикальных составляющих угловых колебаний галопирования φ_у.

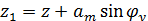
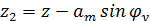
С учетом малости угла φ_у 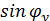= , получаем:

Силы входящие в уравнение вертикальных колебаний определяются:

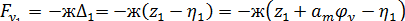
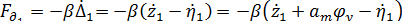
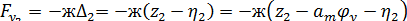
Подставляя в общее уравнение, получим:

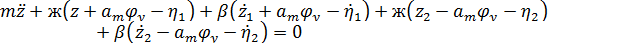
Для вывода уравнения колебания галопирования составим уравнение моментов, которое будет выглядеть следующим образом:

M_ин + M_у1 +M_∂1 + M_у2 + M_∂2 = 0

M_ин = - I_y φ_у

где I_y – момент инерции.

Окончательное уравнение:

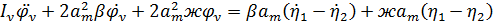
Таким образом колебания рассматриваемой модели описываются двумя уравнениями, эти колебания между собой не связаны. Данная модель позволяет получить различные значения ускорений и перемещений по длине и различные показатели динамики в комплектах рессорного подвешивания.

Дата добавления: 2014-01-04