Составление уравнений вертикальных колебаний моделей с одной степенью свободы при кинематическом возмущении

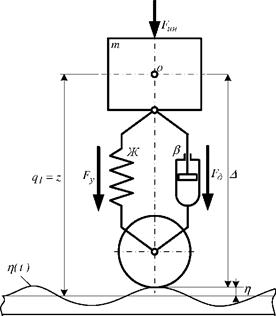
Динамическая модель вагона.

Для исследования динамических свойств вагонов составляют его механическую модель.

Механико-математической (динамической) моделью называют механическую модель вагона описанную системой дифференциальных уравнений.

Динамическая модель должна отражать основные свойства рассматриваемой системы в такой степени, чтобы с её помощью можно было с требуемой точностью оценить динамические качества вагона.

Модель вагона характеризуется набором следующих параметров:

1. инерционные характеристики (массы тел и моменты инерции)

2. характеристики элементов соединения (жесткости и показатели демпфирования)

3. геометрические размеры (длина, высота..)

Положение механической системы может определяться набором k независимых параметров различной физической и кинематической природы, к которым относятся:

· декартовы координаты точек

· расстояния отсчитываемые от траектории

· углы поворота

Число k называют числом степеней свободы, а сами параметры обобщенными координатами q. Простейшей динамической моделью является модель с одной степенью свободы.

Число степеней свободы - это число дополнительных связей, которые необходимо наложить на систему, чтобы сделать равными нулю все возможные перемеще­ния.

Путь считается абсолютно жестким. Данная модель позволя­ет оценить особенности динамиче­ских свойств, определяемых ее структурой и характером возмуще­ния, а также данная модель в первом приближении соответствует вагону с одноступенчатым рессорным подвешиванием.

Масса m на расчетной схеме соответствует сумме масс кузова и тележек, а жесткость Ж и коэффициент затухания β являются эквивалентными характеристиками рессорного подвешивания.

При движении системы, кинематическое возмущение вызывает вертикальные колебания надрессорного строения, которые характеризуются одной обобщенной координатой q₁ = z (подпрыгивание).

В системе действуют силы:

· сила инерции F_ин =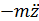

· упругая сила Fy =,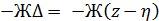

· диссипативная сила F∂ =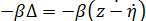

Используя принцип Даламбера, уравнение колебаний рассматриваемой динамической модели записывается

F_ин + Fy + F∂ = 0.

с учетом формул

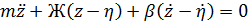
Преобразуем полученное уравнение, перенеся в правую часть члены с возмущающим воздействием

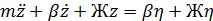
Полученное уравнение представляет собой уравнение вертикальных колебаний модели (колебаний подпрыгивания) с одной степенью свободы, левая часть которого это собственные колебания, а правая - вынужденные (т.к. правая часть - сила от кинематического возмущения).

Решение уравнения колебаний позволит получить значения вертикальных перемещений z, скоростей 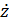и ускорений 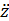массы m и приближенно оценить динамические свойства модели.

Дата добавления: 2014-01-04