Метод Гаусса

Решение.

det A=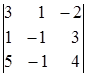==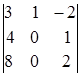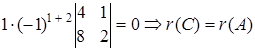<3,

и система имеет бесконечное множество решений.

Найдем минор второго порядка отличный от нуля:.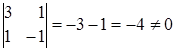

Следовательно, первое и второе уравнения системы являются линейно-независимыми, а третье выражается через первые два, поэтому отбросим третье уравнение. Так как отличный от нуля минор состоит из коэффициентов пр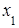и и 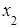, то эти переменные будут базисными, а 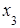– свободной. Получим систему из двух уравнений:

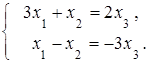
Сложив первое и второе уравнения, получим .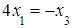

Отсюда ,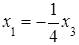

.

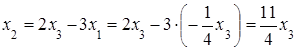Таким образом, решением исходной системы будет:

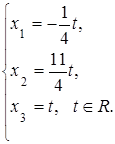
Задавая произвольные значения переменной t, мы получаем каждый раз новое решение исходной системы, то есть система имеет бесконечное множество решений.

Рассмотрим еще один метод решения систем линейных алгебраических уравнений – метод Гаусса, который применим к любой системе линейных алгебраических уравнений. Иногда этот метод называют методом последовательного исключения неизвестных. Заметим, что при использовании этого метода мы также автоматически будем вычислять ранг матрицы системы.

Итак, пусть задана система m линейных алгебраических уравнений с n неизвестными:

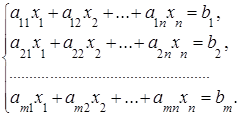(6)

В матричном виде система (6) записывается АХ=В, где А – прямоугольная матрица размера m´n:

А=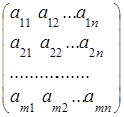, а Х и В – матрицы-столбцы: Х=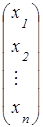, В=.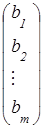

Если в результате преобразований матрицы системы получится треугольная матрица, то система будет иметь вид:

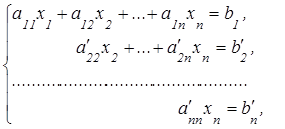
где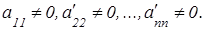

Из последнего уравнения можно найти 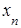, а затем, подставляя найденное 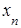в предпоследнее уравнение, найти 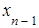и т.д. В итоге будем иметь единственное решение 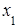, , 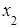…, 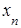. В этом случае ранг матрицы А системы уравнений равен n.

Если в результате преобразований матрицы системы получится трапециевидная матрица, то система примет вид:

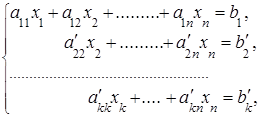
где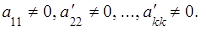

В этом случае k<n, следовательно, система уравнений будет неопределенной, то есть будет иметь бесконечное множество решений, так как она содержит n – k свободных переменных:

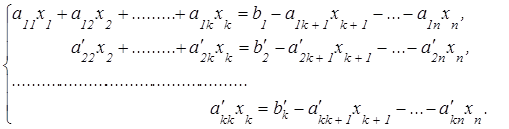
Придавая свободным переменным 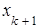, , 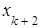…, 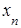произвольные значения, будем иметь каждый раз новое решение исходной системы уравнений, то есть решений будет бесконечное множество. В этом случае ранг матрицы А системы равен k.

Если в результате преобразований получено уравнение, в котором коэффициенты при всех неизвестных равны нулю, а свободный член отличен от нуля, то такая система будет несовместной, то есть не иметь решения.

Следует отметить, что треугольная или трапециевидная форма системы уравнений получалась ввиду предположения, что коэффициенты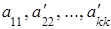отличны от нуля. Если же какой-либо из этих коэффициентов равен нулю, то система уравнений приобретет треугольную или трапециевидную форму лишь после надлежащего изменения нумерации неизвестных.

В заключение отметим, что метод Гаусса применяется и для однородных систем линейных алгебраических уравнений. В этом случае, если получаем треугольный вид системы уравнений, то она будет иметь единственное (нулевое) решение 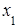==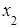 …= =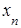0, если же получаем трапециевидный вид системы, то будем иметь бесконечное множество решений.

При решении системы линейных алгебраических уравнений методом Гаусса удобно выписать расширенную матрицу системы и все преобразования выполнять над строками и столбцами расширенной матрицы.

Рассмотрим примеры решения систем линейных алгебраических уравнений методом Гаусса.

Пример 1.

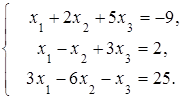
Дата добавления: 2013-12-11