Уравнениеплоской волны

Рис. 1.12. К выводу уравнения бегущей плоской волны

Рассмотрим общий случай, когда распространение колебаний, заданное направляющим вектором n, не совпадает с какой-либо из пространственных осей координат. Пусть в момент времени t=0 в начале координат – точке О, возникают гармонические колебания величины x, описываемые уравнением

.

Благодаря конечной скорости V распространения волны в пространстве, колебания в точке М будут запаздывать во времени по отношению к колебаниям в точке О на время t=ℓ/V, равное времени распространения волны от источника до точки М. С учетом запаздывания волна, распространяющаяся вдоль направления n, описывается уравнением

,

где ℓ – расстояние от начала координат до точки наблюдения. Это расстояние, как видно из рисунка 1.12, равно проекции радиус-вектора r точки наблюдения на направление n:

.

Уравнение (1.53) можно записать так:

.

Полученное уравнение является уравнениемгармонической волны, распространяющейся (бегущей) в направлении, заданном вектором n. Очевидно, что функция, описывающая бегущую волну, содержащая периодическую функцию косинуса или синуса, является периодической функцией двух аргументов: времени t и координаты Х.

· Гармоническаяволна – это волна, соответствующая распространению гармонических колебаний.

· Амплитудаволны – наибольшее значение колеблющейся величины.

· Фазаволны – величина или j=, равная аргументу функции косинуса (или синуса) в уравнении волны.

Отметим, что фаза колебания, приходящего от источника в некоторую точку пространства, увеличивается монотонно и линейно с течением времени, а при увеличении расстояния от источника до точки наблюдения фаза уменьшается.

· Начальная ф азаволны j₀ – фаза в момент времени t=0; очевидно j₀=j(t=0).

Используя общепринятое обозначение для так называемого волнового вектора k (k =w n /V), преобразуем уравнение волны (1.53) к виду:

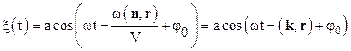
Очевидно, что уравнениеволны распространяющейся вдоль оси Х, имеет вид:

,

или

,

здесь k и i X – волновой вектор и радиус-вектор точки наблюдения с координатой Х.

Несложно показать, что уравнениеволны распространяющейся в направлении, противоположном направлению оси Х, имеет вид:

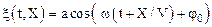. (1.56а)

· Волновойвектор – вектор, определяемый соотношением .

· Волновоечисло – это модуль волнового вектора: . Волновое число показывает, сколько длин волн укладывается на отрезке длиной 2p метров.

Используя понятие волнового числа, уравнению волны бегущей вдоль оси х можно придать симметричный вид:

.

Наконец, учитывая разложение векторов k и r по осям координат: и , запишем уравнение (1.54) следующим образом:

.

Из аналитической геометрии известно, что всякое уравнение первой степени с тремя переменными X,Y,Z вида

(*)

определяет в пространстве плоскость. Сравнение выражения (1.58) с (*) показывает, что коэффициент D играет роль фазы волны и содержит в себе зависимость от времени. Таким образом, уравнение (*) определяет положение некоторой плоскости в каждый момент времени. Во всех точках этой плоскости, называемой волновой поверхностью, фазы волны одна и та же.

1.9.2. Общие характеристики волны

· Волновоеполе – область пространства, в которой существуют колебания.

· Волноваяповерхность – геометрическое место точек постоянной фазы.

· Волновойфронт – волновая поверхность, до которой в данный момент времени распространились колебания. Можно говорить также, что:

· Волновойфронт – поверхность, отделяющая волновое поле от области, в которой еще не началось колебательное движение. Иначе, волновой фронт – геометрическое место точек, до которых к данному моменту времени дошли колебания, таким образом, он является передним краем волны, граничащим с невозмущенной средой.

Форма волновой поверхности зависит от симметрии излучателя: так колебания от точечного источника, распространяющиеся в изотропной и однородной среде, имеют сферический волновой фронт, в иных случаях фронт может иметь вид плоскости, цилиндра и т. п. Соответственные волны называются сферическими, плоскими или цилиндрическими.

· Волновойлуч – линия, определяющая направление распространения колебаний и переноса энергии. В однородной и изотропной среде волновые лучи ортогональны по отношению к волновому фронту. Если волновой фронт плоский, то лучи параллельны между собой.

Как уже отмечено, в волновом поле определена периодическая функция от аргументов t, и X. Найдем период Т волны во времени, для чего используем условие периодичности функции косинуса, и запишем:

,

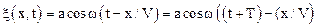что равносильно условию:

,

откуда следует ,

или:

.

Последняя формула показывает, что период волны определяется периодом колебаний источника (ср. (1.52)).

· Периодволны – время, за которое совершается полное колебание в источнике волны.

· Частотаволны – величина обратная периоду колебаний

.

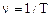Исследуем пространственную периодичность волны. Обозначим пространственный период через l. Используя условие периодичности функции косинуса, можно записать:

.

Это равенство выполняется, если

,

откуда следует, что

,

или

.

Величину l, являющуюся периодом волны в пространстве называют длиной волны.

· Длинаволны – расстояние, на которое распространяется волна за один период колебаний.

Используя определение частоты колебаний n, запишем

Длину волны определяют также как минимальное расстояние между двумя точками пространства, в которых колеблющаяся величина имеет одно и то же значение, поэтому можно дать другое определение:

· Длинаволны есть наименьшее расстояние между точками пространства, в которой колебания происходят в одной фазе.

Уравнение волны позволяет:

· определить значение колеблющейся величины в произвольной точке пространства в произвольный момент времени,

· изучать характер изменения колеблющейся величины в некоторой точке пространства (при фиксированной координате),

· для некоторого фиксированного момента времени позволяет исследовать распределение значений колеблющейся величины в пространстве.

Используя определение периода и длины волны уравнениебегущей волны, взятое, например, в виде (1.56) можно записать следующим образом:

.

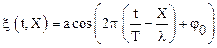1.9.3. Распространение, отражение и преломление волн

Формально процесс распространения волн объясняется принципом Гюйгенса.

· ПринципГюйгенса утверждает: каждая точка среды, до которой доходит волна, становится источником вторичных волн. Поверхность, огибающая в некоторый момент вторичные фронты, указывает положение фронта распространяющейся волны в этот момент времени. Огибающей называют поверхность, касательную ко всем вторичным фронтам.

Принцип Гюйгенса позволяет достаточно просто объяснить явления преломления и отражения волн. В соответствии с принципом, наложение вторичных волн, образованных на границе раздела сред приводит к появлению в первой среде отраженной волны, а во второй – преломленной. Напомним, что в волновой механике направление распространения волны в пространстве задает волновой луч. При наличии отражающих и преломляющих поверхностей используют так называемые углы падения и преломления.

· Уголпадения – это угол между волновым лучем падающей волны и нормалью к границе раздела сред в точке падения.

· Уголпреломления – это угол между нормалью к границе раздела сред в точке падения волнового луча и волновым лучом преломленной волны.

Рассмотрим явление преломления волн. Пусть элемент плоского волнового фронта AС (см. рис. 1.13), распространяясь в однородной среде со скоростью V₁, падает сверху на плоскую границу раздела сред ОО. Предположим, что скорость волны во второй среде V₂ меньше, чем ее скорость V₁ в первой среде. Построим положение огибающей вторичных волн во второй среде для промежутка времени, соответствующего приходу точки С фронта на границу раздела сред. Очевидно, что это время t равно BC/V₁. За время t вторичная волна пройдет во второй среде расстояние AD, равное

V₂t=BC×V₂/V₁.

Рис. 1.13. Преломление волны на границе раздела сред. АС – фронт падающей волны, ВD- фронт преломленной волны

Из чертежа (рис. 1.13) видно, что:

.

Полученный результат позволяет сформулировать закон преломления волн, который утверждает, чтоотношение синуса угла падения к синусу угла преломления равно отношению скорости волны во второй среде к ее скорости в первой среде:

.

Примем без доказательства следующее утверждение: луч падающий, луч преломленный и нормаль, восстановленная в точке падения волны на границу преломляющей среды, лежат в одной плоскости.

Законпреломления волн содержит два утверждения:

· луч падающий, луч преломленный и нормаль, восстановленная в точке падения волны на границу преломляющей среды, лежат в одной плоскости.

· Отношение синуса угла падения к синусу угла преломления равно отношению скорости волны во второй среде к ее скорости в первой среде.

Соотношение (1.64) есть математическое выражение закона преломления.

Рассмотрим теперь явление отражения волн. Пусть часть плоского волнового фронта AF (см. рис. 1.14), распространяясь в однородной среде со скоростью V, падает на плоскую отражающую поверхность ОО.

Построим огибающую вторичных отраженных волн в момент времени, когда точка F фронта достигнет отражающей поверхности в точке В. К этому моменту времени весь участок фронта AF полностью отразится от поверхности ОО. Вторичные сферические волны будут иметь различные радиусы, поскольку они начинают распространяться в различные моменты

Рис. 1.14. Отражение волны от плоской поверхности

времени, соответственно достижению точками фронта поверхности ОО. Радиусы полусфер равны расстояниям, которые проходят фронты вторичных волн от их источников, расположенных на границе раздела сред. Для волны, испущенной в точке А, радиус фронта равен AD, для точки Е он равен EG, для точки В – нулю. Из равенства треугольников AFB и ADB следует, что угол падения a равен углу отражения b.

· Законотраженияволн, как и закон преломления, содержит два утверждения:

1. Луч падающий, луч отраженный и нормаль, восстановленная в точке падения волны на границу преломляющей среды, лежат в одной плоскости.

2. Угол падения волны на отражающую поверхность равен углу отражения.

Математическое выражение закона отражения таково:

a=b.

1.9.4. Продольные и поперечные волны

Как отмечалось ранее, в колебаниях могут участвовать физические величины различной природы, что обуславливает существование различных типов волн. Различие в характере проще всего понять на примере упругих механических волн – волн, в которых частицы среды колеблются в зависимости от амплитуды, частоты и направления колебаний соседних частиц. Колебания частиц вещества могут происходить как в направлении волнового луча, так и в направлении перпендикулярном ему. В первом случае волны называют продольными; продольные волны могут распространяться в веществе в любом агрегатном состоянии: твердом, жидком, газообразном и плазменном.

· Продольныеволны – волны, в которых колеблющаяся величина периодически изменяется в направлении распространения волны.

На рисунке 1.15 показано как при движении частиц, участвующих в продольных колебаниях образуются чередующиеся области их сгущения или разрежения. Длина изображенной на нем волны соответствует расстоянию между двенадцатью частицами.

Рис. 1.15. Рапространение продольных колебаний в упругой среде

· Поперечныеволны – это волны, в которых колеблющаяся величина изменяется в направлении перпендикулярном направлению распространения волны.

Поперечные упругие (механические) волны могут распространяться только в твердых телах, поскольку лишь в них могут возникать напряжения сдвига. Движение частиц в поперечной волне показано на рисунке 1.16.

Рис. 1.16. Распространение поперечной волны

Вдоль волнового луча расположены чередующиеся группы частиц, смещенные вверх или вниз и образующие бугры и впадины[2]. Скорость распространения гармонических волн зависит от упругих свойств среды, но не зависит от частоты и амплитуды колебательного движения частиц среды.

· При переходе волны из одной среды в другую ее частота не изменяется, но за счет различной скорости распространения колебаний изменяется длина волны.

Из рисунков 1.15 и 1.16 видно, что и в продольной, и в поперечной волне частицы среды не движутся в направлении распространения волны, а совершают колебания относительно положения равновесия, которое, в среднем, остается неизменным. Движение каждой последующей частицы, вовлекаемой в колебательный процесс, отстает по фазе от предыдущей. Это вызывает кажущийся эффект поступательного движения гребней и впадин волны (но не частиц! среды). Конечная скорость V передачи взаимодействий частиц среды вызывает запаздывание волны (в точке наблюдения с координатой х) во времени на величину t=x/V.

1.9.5. Интерференция волн

Если в веществе распространяются волны малой амплитуды, то, проходя одновременно через некоторую область пространства, они подчиняются принципу суперпозиции. При наложении друг на друга волны не искажаются: разойдясь, они не несут на себе следов прошедшего взаимодействия. Суперпозиция волн приводит к характерным для волнового движения явлениям: интерференции и дифракции.

· Интерференция – явление наложения в волновой зоне конечного числа (двух или более) волн, в результате чего в различных точках пространства происходит усиление или ослабление амплитуды результирующей волны.

· Дифракция – любое отклонение волн от прямолинейного распространения, в узком смысле – это огибание волнами препятствий.

· Когерентнымиволнами называют волны, имеющие одинаковую частоту и неизменную во времени разность фаз для всех точек пространства.

Рассмотрим процесс наложения двух плоских когерентных волн с частотой w, распространяющихся от источников I₁ и I₂. Предположим, что амплитуды волн А равны между собой, начальные фазы колебаний источников равны нулю. Волны (см. рис. 1.17) проходят до точки наблюдения М различные пути S₁ и S₂, и возбуждают в ней колебания, которые описываются уравнениями:

.

В формулах (1.65) величина t соответствует времени, прошедшему от начала работы источников волн, V – скорость распространения волн.

Рис. 1.17. К расчету интерференционного поля

При условии, что оба колебания происходят в одном направлении, амплитуда результирующего колебания в точке М может быть определена на основании принципа суперпозиции (см. (1.40)):

.

Из соотношения (1.66) видно, что амплитуда А_Р колебаний в точке наблюдения при прочих, указанных выше условиях зависит от величины слагаемого , а конкретней, от множителя cosd.

Величину называют интерференционным членом, d=Ф₂-Ф₁ – разностьюфаз Ф₁ и Ф₂ колебаний, вызванных первой и второй волной в точке наблюдения:

.

Интенсивность волны I пропорциональна квадрату ее амплитуды A, т. е. I~A², поэтому для интенсивности результирующего колебания (см.(1.66)) можно записать:

.

Величину D=S₁-S₂ называют разностьюхода волн. Очевидно, что при условиях, указанных выше, разность хода D и разность фаз d определяются положением точки М, а значит, в различных точках пространства результирующее колебание будет иметь различную амплитуду и интенсивность. Таким образом, при наложении когерентных волн в волновом поле образуется некоторое распределение интенсивности колебаний, а значит, – неравномерное распределение энергии колебаний. Распределение амплитуды результирующего колебания, характеризуемое положением минимумов и максимумов колебаний, дает интерференционную картину. Интерференционная картина неподвижна, несмотря на то, что она образована бегущими волнами. Это связано с тем, что для когерентных волн разность фаз колебаний d в точке М, а, значит, и амплитуда колебаний остается постоянной с течением времени.

В зависимости от знака интерференционного члена (знака функции косинуса) интенсивность колебаний в точке наблюдения М может быть больше суммы интенсивностей I₁ и I₂ колебаний от источников (если cosd>0), или меньше этой суммы (cosd<0). Особенно отчетливо интерференция наблюдается при равенстве интенсивностей налагающихся волн: I₁=I₂, в этом случае наибольшее значение I равно 2I₁, наименьшее – нулю.

Вернемся к формуле (1.67), которую запишем, используя разность хода, как

.

Проведем следующие преобразования

.

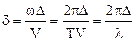Из последнего следует, что если разность хода D для некоторой точки наблюдения М равна целому числу длин волн D=nl, то разностьфаз d будет кратна 2p (d=2pn); в этом случае говорят, что разностьфаз составляет четое число p. Колебания, возбуждаемые первой и второй волной в этой точке, будут происходить синхронно и амплитуда колебаний в ней будет наибольшей: в точке М располагается интерференционный максимум.

Условие (1.70) окончательно можно сформулировать так:

· интерференционныймаксимум в некоторой точке пространства наблюдается при условии, что разность хода волн до нее составляет целое число длин волн (или четное число длин полуволн):

.

Несложно видеть, что если разность хода волн составляет нечетное число длин полуволн, то в точке наблюдения имеется интерференционныйминимум:

,

здесь l – длина волны в среде, в которой распространяются волны. Из соотношений (1.70) и (1.71) следует, что в этом случае разность фаз равна нечетному числу p, т. е.

.

Если разность фаз d колебаний в точке М меняется случайным образом, то в результате усреднения по времени (время усреднения много больше периода колебаний) интерференционный член обращается в ноль, поскольку среднеезначение косинуса равно нулю. В этом случае соотношение (1.66) дает

,

или

,

т. е. интерференционная картина отсутствует, и в точках пространства наблюдается равномерное распределение энергии колебаний.

1.9.6. Стоячие волны

Стоячая волна– периодические во времени синфазные колебания с характерным распределением амплитуды колебаний: чередованием узлов – областей с амплитудой колебаний равной нулю и пучностей – областей, в которых амплитуда максимальна. Стоячая волна может быть представлена как результат наложения (суперпозиции) двух бегущих навстречу друг другу волн одной частоты.

Пусть источник колебаний помещен в пространственно ограниченную среду и работает постоянно, излучая волны, причем созданы условия для их отражения на границе, например, в заполненной воздухом трубе с закрытым или открытым концом. Предположим, что отсутствует диссипация энергии, так что амплитуда падающей и отраженной волны одинаковы.

Произвольная частица среды, имеющая координату Х, участвует в двух механических колебаниях, возбужденных волнами. Без ущерба для общности положим начальную фазу колебаний источника равной нулю. Смещения частицы в точке с координатой Х, согласно (1.56) и (1.56а) определяются формулами:

Результирующее смещение по принципу суперпозиции равно:

.

Величина x колеблется с постоянной во времени циклической частотой w, но с зависящей от координаты Х точки наблюдения амплитудой. Амплитуда колебаний равна:

.

Волна, описываемая уравнением(1.75), называется стоячей волной. Легко видеть, что в некоторых точках оси Х, вдоль которой распространяется волна, амплитуда колебаний тождественно равна нулю, т. е. в этих точках отсутствуют смещения частиц. Точки, в которых амплитуда стоячей волны равна нулю, называются узловыми точками или "узлами" волны.

· Узел стоячей волны – точка пространства, в которой амплитуда колебаний тождественно равна нулю.

Используя уравнение (1.76), найдем координаты узлов для стоячей волны. Из условия следует:

,

где n=0, ±1, ±2, ±3… – любое целое число и ноль. Выражая из последнего равенства координаты узлов, имеем:

.

Очевидно, что максимальное значение амплитуды колебаний (А=2а) достигается в точках пространства, координаты которых удовлетворяют условию:

.

Такие точки называются "пучностями" волны.

· Пучность стоячей волны – точка пространства, в которой амплитуда колебаний достигает максимального значения.

Найдем координаты пучностей. Из условия (1.78) следует, что

откуда

,

где n любое целое число и ноль. Как показывают соотношения (1.77) и (1.79), координаты узлов и пучностей не меняются с течением времени при условии, что длина волны не изменяется. В точках пространства, координаты которых не удовлетворяют условиям минимума и максимума, величина амплитуды колебаний имеет промежуточные значения из интервала [0,2а].

Единство колебаний и волн проявляется в колебательных процессах в струнах, стержнях и трубах. Так, в заполненной воздухом трубе с закрытым или открытым концом устанавливается стоячая волна со следующей картиной расположения узлов и пучностей.

Рис. 1.18. Стоячие волны в струне и трубе

Отметим некоторые особенности стоячей волны. В отличие от бегущей волны, вызывающей последовательно одинаковые смещения частиц среды, смещения частиц в стоячей волне отличаются друг от друга. В бегущей волне все точки имеют различную фазу. Когда одни точки достигают максимального отклонения, другие проходят положение равновесия и т. п. Такую волну можно представлять себе как синусоиду, движущуюся вдоль волнового луча. В стоячей волне колебания частиц происходят иначе. В некоторые моменты времени все частицы среды одновременно проходят положение равновесия.

Действительно, из (1.75) следует, что xº0 при условии coswt=0. Последнее равенство выполнено, если

, (n=0,1,.2, 3….целое).

Используя определение периода колебаний, получим

, (n=0,1,.2, 3….целое).

Из последнего соотношения следует, что в моменты времени t, удовлетворяющие условию

,

значение колеблющейся величины во всех точках пространства оказываются равными нулю.

Если ½coswt½=1, или wt=np, где n=0,1,.2, 3… произвольное целое число, то колеблющаяся величина во всех точках пространства (исключая узлы) одновременно приобретает свое наибольшее значение, зависящее от соответствующей координаты. Этому состоянию соответствуют моменты времени t=np/w.

.

Рис. 1.19. Стрелки показывают направление скорости частиц. Наклонная линия в левой части рисунка демонстрирует распространение постоянной фазы. Временной масштаб рисунка равен T/8

Рисунок 1.19 показывает различие в движении частиц бегущей и стоячей волны. Соотношения (1.77) и (1.79) позволяют утверждать, что расстояние между узлами и пучностями стоячей волны одинаково и равно половине длины бегущей волны той же частоты. При переходе через произвольный узел величина 2Аcos(wX/V) меняет знак, что означает: частицы среды, лежащие по разные стороны от узла, колеблются в противофазе.

Частицы среды, заключенные между двумя соседними узлами, совершают синфазные колебания.

В стоячей волне не происходит переноса энергии в пространстве, а лишь перекачка одного вида энергии в другой с частотой в два раза большей, чем частота бегущей волны. Дифференцируя уравнение (1.75) стоячей волны в упругой среде по времени и координате найдем формулы для скорости колеблющихся частиц среды и величины относительной деформации среды:

,

.

Эти формулы имеют вид, аналогичный уравнению (1.75), а значит, описывают стоячие волны скорости и деформации. Очевидно, что смещение и деформация колеблются в фазе, например, одновременно достигают максимума, при этом скорость частиц среды обращается в ноль.

1.9.7. Эффект Доплера

В соответствии с принципом Доплера, волна, испущенная источником, распространяется в пространстве независимо от своего источника. Скорость ее распространения определяется характером волны и свойствами среды, и не зависит от скорости движения источника. Однако, частота (и длина волны) зависит как от скорости источника, так и от скорости наблюдателя (приемника), регистрирующих волну.

· Изменение частоты волны, воспринимаемой наблюдателем в зависимости от относительного движения источника волн и самого наблюдателя, носит название эффектаДоплера. Если источник волны и/или наблюдатель, ее воспринимающий, движутся относительно среды, в которой распространяется волна, то частота, измеряемая наблюдателем, будет зависеть не только от частоты посылаемой волны, но также от направления и скоростей движения, как источника, так и наблюдателя.

А	В
Рис. 1.20. Волновые поверхности неподвижного (А) и движущегося (В) источника

Получим количественные соотношения для эффекта Доплера в простейшем случае, когда источник колебаний и наблюдатель движутся вдоль одной и той же оси Х. Обозначим: V – скорость распространения волны, V _И и V _Н – скорости источника и наблюдателя в некоторой инерциальной системе отсчета. Источник I, находящийся в начале координат в момент времени =0 начинает излучать волны с частотой n₀.

Рис. 1.21. К эффекту Доплера

Рассмотрим случай, когда источник движется в направлении оси Х со скоростью, удовлетворяющей условию V_И<V. Пусть за время t волновой фронт достиг точек М₁ и М₂ оси Х с координатами ±Vt. Предположим, что в точках М₁ и М₂ находятся неподвижные наблюдатели, измеряющие частоту приходящей волны. За время t источник переместится в положение I₁, с координатой V_Иt. При частоте колебаний источника n₀ за это время будет испущен цуг волн длиной (V-V_И)t в направлении оси Х и длиной (V+V_И)t в направлении, противоположном оси Х. Эти цуги содержат N=n₀t волн. Длина волны в направлении оси Х равна:

.

Используя определение длины волны, запишем

.

Последнее соотношение позволяет найти частоту волны воспринимаемой наблюдателем в М₁:

.

Аналогичным образом получим частоту волны, регистрируемой наблюдателем, находящимся в точке М₂:

.

Рассмотрим теперь случай, когда источник волн неподвижен, а наблюдатель М₁ приближается к источнику со скоростью V_H. Частота источника по-прежнему равна n₀. За время t мимо неподвижного наблюдателя прошел бы цуг волн длиной Vt, содержащий N=n₀t волн. В результате встречного движения наблюдатель зарегистрирует дополнительные волны укладывающиеся на пройденном им пути V_Нt. Число таких волн равно:

,

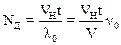здесь l₀ длина волны неподвижного источника.

Полное число зарегистрированных за время t волн будет равно:

.

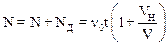Частота волны для такого наблюдателя равна:

.

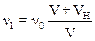Для наблюдателя удаляющегося от источника частота n₂ будет равна

.

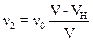Формулу для частоты волны, регистрируемой при совместном движении наблюдателя и источника можно получить, если в соотношениях (1.84) и (1.85) вместо n₀ использовать значения частоты, определяемые формулами (1.86) и (1.87):

.

Верхний знак необходимо записывать, если источник и наблюдатель приближаются друг к другу, нижний – когда удаляются.

Глава 2. Динамика

2.1. Первый закон Ньютона. Инерциальные системы отсчета. Принцип относительности

I-йзаконНьютона: существуют такие системы отсчета, в которых тело движется равномерно, прямолинейно или покоится, если на него не действуют другие тела.

Из опыта известно, что в разных системах отсчета движение тела и законы, описывающие его, могут выглядеть по-разному. Опыт показывает, что всегда можно выбрать

инерциальную систему отсчета, которую для краткости сокращенно обозначают ИСО.

Инерциальнаясистемаотсчета, – система отсчета, которая или покоится, или движется прямолинейно и равномерно.

По отношению к инерциальной системе отсчета пространство однородно и изотропно, а время однородно. В инерциальной системе отсчета изолированная материальная точка или покоится, или бесконечно долго движется поступательно – равномерно и прямолинейно в соответствии с уравнениями:

,

здесь V ₀, r ₀ – начальная скорость и радиус-вектор начального положения движущейся материальной точки.

· Однородностьпространства означает эквивалентность всех его точек.

· Изотропность пространстваозначает эквивалентность всех направлений в пространстве.

· Однородностьвремени означает, что все его моменты физически эквивалентны.

Строго инерциальных систем, по-видимому, не существует. Система отсчета, связанная с Землей – геоцентрическая – не является неинерциальной, так как Земля вращается вокруг своей оси и вокруг Солнца. Гелиоцентрическая система отсчета – тоже, поскольку Солнечная система совершает сложное движение около центра Галактики. Но при решении большинства практических задач обе эти системы с большой точностью можно считать инерциальными.

· ПринципотносительностиГалилея: законы механики имеют одинаковый вид во всех инерциальных системах отсчета.

Отсюда следует равноправие всех инерциальных систем отсчета: механическими опытами нельзя установить движется система отсчета прямолинейно и равномерно или покоится.

2.1.1. Классический законсложения скоростей

Пусть некоторая система К' (X',Y',Z',O') движется равномерно и прямолинейно относительно другой, неподвижной системы К (X,Y,Z,O), со скоростью V ₀.

Рис. 2.1. К преобразованию скоростей.

Как видно из рисунка 2.1, справедливо равенство:

,

где r – радиус-вектор точки М в неподвижной системе отсчета, r ^I – радиус-вектор точки М в подвижной системе отсчета К' и R – радиус-вектор начала подвижной системы отсчета относительно неподвижной. Если предположить, что в начальный момент времени начала координат систем К и К^I совпадают, то вектор R=V ₀t.

С учетом последнего замечания дифференцирование (2.2) по времени дает

.

Формула (2.3) – математическое выражение классического закона сложения скоростей, где V – скорость материальной точки М относительно неподвижной СО, V _I – скорость точки М относительно подвижной СО и V ₀ – скорость подвижной СО относительно неподвижной.

В проекциях на оси координат X, Y, Z (2.3) записывается так:

Последнее уравнение системы выражает представление об абсолютном времени, которое течет равномерно и одинаково во всех инерциальных системах отсчета.

2.2. Второй законНьютона

· Ускорение а, с которым движется материальная точка, прямо пропорционально векторной сумме всех сил, действующих на нее, и обратно пропорционально ее массе:

.

Уравнение (2.5) является основным уравнениемдинамики поступательного движения материальной точки (тела). С формальной точки зрения оно представляет собой векторное дифференциальное уравнение второго порядка.

Во втором законе динамики появились два новых понятия: сила и масса.

· Масса – является мерой инертных и гравитационных свойств тела.

Понятие "масса" для обозначения физической величины, характеризующей инерционные и гравитационные свойства тел, ввел И. Ньютон в "Началах натуральной философии". Инертная m_И масса тела входит в уравнении второго закона Ньютона (2.5), она характеризуют способность тела отвечать определенным ускорением на действие определенной силы. Гравитационная масса m_ГР – входит в закон всемирного тяготения (см. далее (2.6)), она характеризуют способность тела притягивать другие тела.

До настоящего времени физическая природа массы и причины ее вызывающие не выяснены, эти проблемы относят к фундаментальным проблемам современной физики. Исследования позволили сформулировать

· принципэквивалентности: инертная и гравитационная массы равны между собой. В ходе экспериментов, проведенных в 1971 году, точность[3], с которой доказана справедливость принципа эквивалентности, была доведена до 10 ¹². На этом основании, в дальнейшем используется термин масса, безотносительно к ее физической природе.

· Сила – векторная величина, являющаяся количественной характеристикой механического воздействия одного тела на другое.

В результате механического воздействия на тело у него появляется ускорение или происходит его деформация.

2.3. Силы в механике

Основные силы, действие которых рассматривает механика Ньютона следующие:

2.3.1. Сила всемирного тяготения

· Законвсемирноготяготения:

все тела притягивают друг друга. Сила(всемирного тяготения), с которой две материальные точки притягивают друг друга, пропорциональна произведению масс этих точек и обратно пропорциональна квадрату расстояния между ними.

Математическое выражение закона всемирного тяготения имеет вид:

,

здесь g=6,670·10^-11 м³/кг·с² – гравитационная постоянная.

Физический смысл гравитационной постояннойG состоит в следующем: она показывает силу, с которой притягивается материальная точка массой 1 кг к другой такой же точке, находящейся на расстоянии одного метра. Векторная форма записи закона всемирного тяготения такова:

,

здесь F ₁₂ сила, действующая на первую материальную точку со стороны второй, e ₁₂- единичный вектор, направленный от первой точки ко второй (см. рис. 2.2).

Рис. 2.2. К закону всемирного тяготения.

Вычисление силы, с которой притягиваются тела произвольной формы, представляет собой сложную математическую задачу, которая имеет аналитическое представление:

,

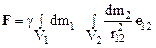интегрирование ведется по объему V₁ первого и второго V₂ тела, r ₁₂ радиус-вектор, направленный из элементарной массы dm₁ первого тела к элементарной массе dm₂ второго тела.

Расчеты на основании соотношения (2.8) показывают, что формулу (2.6) можно использовать в случае взаимодействия шаров, в этом случае величина r равна расстоянию между центрами шаров. Формулу (2.6) можно применять при учете гравитационного взаимодействии шарообразной Земли и тела произвольной формы, которое можно считать материальной точкой по сравнению с размерами Земли.

Закон всемирного тяготения позволил теоретически обосновать три эмпирических законаКеплера, описывающие движение планет:

1. Траектория планеты представляет собой эллипс, в одном из фокусов которого находится Солнце.

2. Радиус-вектор планеты за равные промежутки времени описывает одинаковые площади.

3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит.

Сила всемирного тяготения, называемая также гравитационной силой является одной из фундаментальных сил в природе. Универсальный характер силы тяготения обуславливает ее большую роль в явлениях природы. Приведем дополнительно некоторые характеристики силы всемирного тяготения.

Дата добавления: 2013-12-12