Решение задач по динамике движения материальной точки по окружности. Это уравнение является одним из основных уравнений динамики вращательного движения материальной точки

.

Получаем:

.

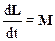Это уравнение является одним из основных уравнений динамики вращательного движения материальной точки. Оно является следствием и аналогом уравнения (2.31) d P /dt= F.

Из соотношения (2.40) следует, что под воздействием приложенного момента сил М ¹0 момент импульса материальной точки изменяется таким образом, что

.

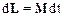Соотношение (2.41) выражает закон изменения момента импульса. Очевидно, что вектор приращения момента импульса d L направлен параллельно вектору М момента силы.

Выражение момента импульса можно представить в следующем виде:

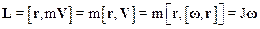
Обратим внимание на то, что соотношения (2.37) и (2.40) получены нами для материальной точки.

2.7. Динамика вращательного движения

относительно неподвижной оси

В предыдущем разделе рассмотрено вращательное движение материальной точки. Многие понятия этого раздела легко обобщаются на случай вращательного движения твердого тела конечного размера. Вращательным движением твердого тела называют движение, при котором все точки тела описывают окружности в плоскостях, перпендикулярных оси вращения, при этом их центры лежат на оси вращения. Для кинематического описания вращательного движения достаточно определить в пространстве положение оси вращения, величину угловой скорости, углового ускорения и использовать уравнения кинематики вращательного движения.

Рассмотрим систему, состоящую из n материальных точек. На объекты системы могут действовать внутренние силы, т. е. силы, определяемые взаимодействиями объектов между собой, и внешние силы – силы со стороны тел, не входящих в систему. Для i-й материальной точки механической системы (тела) можно записать уравнение вида (2.40):

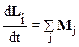, (j=1, 2, …, n).

Запишем аналогичные уравнения для всех элементов системы и сложим их почленно:

.

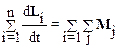Преобразуем левую часть полученного уравнения:

,

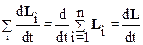где d L /dt=Sd L _i/dt – момент импульса системы. Отметим, что соотношение (2.43) указывает на аддитивность момента импульса.

Используя третий закон Ньютона и аддитивность момента сил, легко показать, что суммарный момент внутренних сил равен нулю. Таким образом, двойная сумма в правой части уравнения (2.42) равна результирующему моменту внешних сил:

.

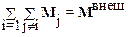С учетом сказанного уравнение (2.42) принимает вид:

.

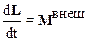Это уравнение отличается от уравнения (2.29), записанного для одной материальной точки тем, что теперь L – это момент импульса системы материальных точек относительно точки. Однако, как и для отдельной точки,

· скорость изменения момента импульса механической системы равна моменту внешних сил, действующих на нее.

Если рассматривать вращение системы относительно оси Z, то уравнение (2.45) преобразуется следующим образом:

,

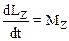где L_Z момент импульса системы относительно оси вращения Z, M_Z – суммарный момент внешних сил относительно той же оси.

Твердое тело, вращающееся вокруг неподвижной оси с постоянным угловым ускорением (e_z = const), можно рассматривать как механическую систему, образованную совокупностью бесконечно малых материальных точек dm. Таким образом, результаты, полученные выше для механической системы, можно использовать при описании движения твердого тела. В частности, применимо уравнение(2.37) в векторнойили скалярной форме:

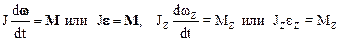
2.7.1. Момент инерции твердого тела

Момент инерциитвердого тела – величина аддитивная. Момент инерции твердого тела относительно некоторой оси равен арифметической сумме моментов инерции частиц, составляющих это тело, относительно той же оси:

,

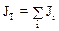здесь J_i – момент инерции i-ой частицы, на которые можно мысленно разбить тело. Говоря иначе, момент инерциитвердого тела относительно некоторой оси равен сумме произведений элементарных масс dm_i тела на квадраты расстояний этих масс от той же оси вращения:

.

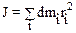Для твердого тела, с непрерывным распределением вещества, момент инерции находят интегрированием по объему V, занятым телом:

,

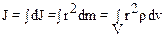где dm=rdV, r – плотность тела, dV – элементарный объем.

B качестве примера вычислим момент инерции однородного диска относительно оси симметрии, перпендикулярной плоскости диска (см. рис. 2.17). Пусть толщина диска h, радиус R, плотность r. Для вычислений воспользуемся полярной системой координат r,j. Элементарная масса частицы диска равна dm=rhrdrdj, элементарный момент инерции dJ==rhr³drdj. Используя (2.49) запишем:

.

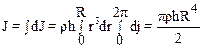Произведение prhR² равно массе М диска, окончательно

.

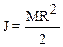Рис. 2.17. К вычислению момента инерции диска.

Момент инерции однородного тела вращения с некоторой образующей, заданной функцией f(z), вычисляется следующим образом. Пусть твердое тело имеет плотность r. Тогда (см. (2.49))

,

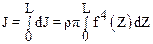где L – длина тела вращения.

Таблица 2

Моменты инерции некоторых тел правильной геометрической формы

Тело	Ось, относительно которой определяется момент инерции	Формула момента инерции
Однородный тонкий стержень массой m и длиной L	Проходит через центр тяжести стержня перпендикулярно стержню	mL^2/12
Проходит через конец стержня перпендикулярно стержню	mL^2/3
Тонкое кольцо, обруч, труба радиусом R и массой m, маховик радиусом R и массой m, распределенной по ободу	Проходит через центр перпендикулярно плоскости основания	mR^2
Круглый однородный диск (цилиндр) радиусом R и массой m	Проходит через центр диска перпендикулярно плоскости основания	mR^2/2
Однородный шар массой m и радиусом R	Проходит через центр шара	2mR^2/5

ТеоремуШтейнера примем без доказательства:

· момент инерции тела J относительно оси, не проходящей через его центр масс, равен сумме двух слагаемых. Первое слагаемое равно моменту инерции тела J₀ относительно оси, проходящей через центр масс и параллельной данной. Второе слагаемое – произведение массы тела на квадрат расстояния b между осями:

J = J₀+mb².

Пример 2.4.

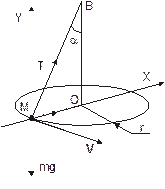
Определить угол между вертикальной осью конического маятника и нитью, если тело движется с постоянной угловой скоростью w. Длина невесомой нити подвеса L.

Решение

a=?

w, L, g=9,8 м/с²

Пусть масса конического маятника равна m. Движение материальной точки происходит в горизонтальной плоскости под действием силы натяжения нити Т и силы тяжести m g (см. рисунок).

Основной закон динамики для данной задачи имеет вид:

m a = Т + m g. (1)

Выберем начало системы координат в центре движущегося по окружности тела так, чтобы ось Х проходила через центр окружности, а ось Y направим вверх. Проецируя уравнение (1) на оси, имеем:

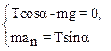(2)

Нормальное ускорение материальной точки а_n = w²r. Из чертежа следует, что радиус траектории маятника r=ОМ равен r=Lsina, где L=МВ – длина подвеса. Используя дополнительные соотношения, преобразуем уравнения системы (2):

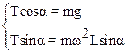(3)

Из уравнений (3) следует:

cosa = g/w²L,

или

a = arccos(g/w²L).

Пример 2.5.

На веревке длиной R = 1м висит груз массой m = 5 кг. Максимальное натяжение, которое может выдержать веревка, TMAX = 60 Н. Оборвется ли веревка, если ее отклонить на угол a = 30°? На какой максимальный угол можно отклонить веревку, чтобы она не разорвалась?

aMAX=? ОА=R=1м, m=5 кг, TMAX=60 H, a=30°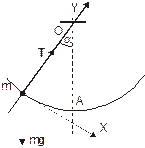

Решение.

На груз m действуют две силы: сила тяжести m g и сила натяжения Т. Основной закон динамики принимает вид:

m a = m g + Т. (1)

Выберем начало системы координат в центре движущегося по окружности тела так, чтобы ось Y проходила через центр окружности, а ось Х направим по касательной.

Проецируя уравнение (1) на оси Y и X имеем:

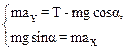(2)

Ускорение а_х, входящее во второе уравнение системы (2) представляет собой тангенциальное ускорение и указывает, что модуль скорости движущегося тела меняется с течением времени. Сила натяжения Т в точке А определяется первым из уравнений (2):

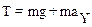(3)

Ускорение a_Y, есть нормальное или центростремительное, ускорение а_n. Очевидно, что максимальное натяжение веревка испытывает в точке А, так как в этой точке тело имеет максимальную скорость, а значит – максимальное нормальное ускорение. Используя выражение a_Y=а_n=V²/R для нормального ускорения, преобразуем уравнение (3):

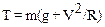(4)

Скорость тела в точке А можно определить с помощью закона сохранения механической энергии. В точке наибольшего отклонения полная механическая энергия – это потенциальная энергия е_П = mgh, где h = R(1- соsa). В точке А механическая энергия равна кинетической (за нулевой уровень потенциальной энергии удобно принять уровень соответствующий нижней точке А). Уравнение закона сохранения энергии запишем так:

.

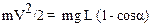Откуда получим, что квадрат скорости с точке А равен

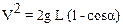. (5)

Подставляя в (4) выражение (5) получим окончательно для силы натяжения:

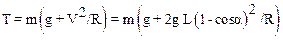. (6)

Подставляя в (6) максимальное значение силы Т=Тmax можно определить угол при котором веревка оборвется, т. к. достигается предельное усилие. Расчеты дают что a_max=45°.

Итак, если веревку отклонить на 30°, то она не оборвется.

Пример 2.6.

Тело скатывается с вершины гладкой сферической поверхности радиуса R. Найти, при какой скорости тело оторвется от поверхности. Считать, что трение отсутствует.

Решение.

H=? R m=0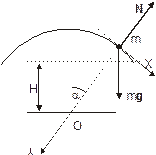

На скользящее тело действуют сила тяжести m g и сила N нормальной реакции полусферы. Уравнение движения имеет вид

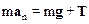. (1)

Направим ось Х по касательной поверхности полусферы, ось Y – радиально в направлении ее центра. Проецируя уравнение (1) на оси получим:

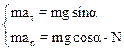
Преобразуем полученные уравнения.

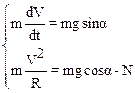(3)

Если учесть, что время движения dt может быть вычислено по формуле dt=dℓ/V, где dℓ=Rda, то первое уравнение приводится к следующему виду

.

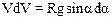Интегрируя последнее по V и a, получим соотношение

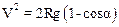. (4)

В момент отрыва тела от полусферы реакция опоры обращается в ноль, и второе из уравнений (3) принимает вид

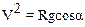(5)

исключив a из соотношений (4) и (5) найдем

.

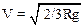Пример 2.7.

Найти максимальную разность между силами натяжения нити при вращении в вертикальной плоскости шарика массой m на невесомой нити.

Решение

(Т1-Т2)МАХ=? m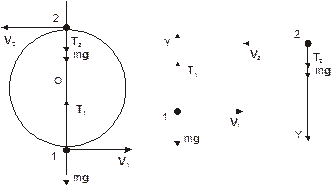

На шарик действуют две силы: сила натяжения Т и сила тяжести m g. Уравнение движения (второй закон Ньютона) запишется так:

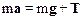. (1)

Для нахождения максимальной разности между силами натяжения, возникающими при вращении шарика, вычислим силы натяжение нити в точках 1 и 2.

Для положения 1 уравнение движения в проекции на оси координат "1" запишется в виде:

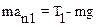, (2)

где .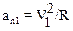

Аналогично, в положении 2 для проекций в системе координат "2" имеем:

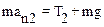. (3)

так как 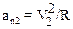, то из (2) и (3) имеем

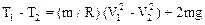(4)

Разность 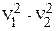определим из закона сохранения энергии. Если выбрать за нулевой уровень отсчета потенциальной энергии уровень точки 1, то можно записать, что

.

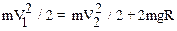Следовательно,

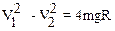. (5)

Подставляя (5) в соотношение (4) имеем окончательно

.

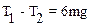Пример 2.8.

Вал в виде сплошного цилиндра массой m=10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m₁=2 кг. С каким ускорением a будет опускаться гиря, если её предоставить самой себе.

a=?

m=10 кг, m₁=2 кг

Решение

В задаче участвуют два тела, совершающие различные движения: тело m₁ движется прямолинейно, вал – вращается. Уравнения движения имеют следующий вид:

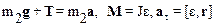, (1)

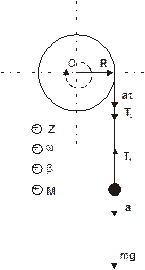
в системе уравнений (1) введены обозначения: а _t – тангенциальное ускорение точек на периферии вала, Т – сила натяжения шнура, r – радиус вала, М – момент, вращающий вал, а – ускорение тела m₁.

Момент, вращающий вал равен 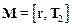, J – момент инерции вала относительно геометрической оси. Рассматривая вал как однородный цилиндр, считаем, что его момент инерции равен J = 1/2m₁r².

Определим направление векторных величин (по правилу буравчика) и выбрав направление осей координат как показано на рисунке запишем систему (1) в проекциях.

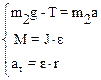(2)

При условии, что шнур нерастяжим и отсутствует его скольжение по поверхности вала тангенциальное ускорение а _t по модулю равно поступательному ускорению а груза m₁: а_t=а. С учетом дополнительных соотношений уравнения системы (1) примут вид:

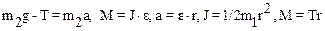(3) Решая систему относительно ускорения a получим:

.

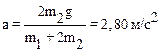Пример 11.

Через блок в виде диска, имеющий массу m=80г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m₁=100г и m₂=200г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.

Решение.

а1, а2=? m=80 г=8×10^–2 кг m1=100 г =10^–1 кг m2=200 г=2×10^–1 кг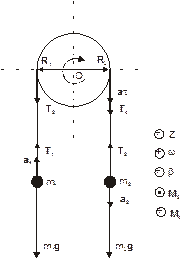

Рассматриваемая в задаче система состоит из двух движущихся поступательно грузов и одного вращающегося диска. На каждый из грузов действует две силы: сила тяжести m g, направленная вниз, и сила Т натяжения нити, направленная вверх. Запишем законы поступательного и вращательного движения этих тел.

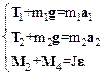(1)

Результирующий вращающий момент, приложенный к диску, равен

М = М ₂+ М ₄=[ R ₁, T ₂]+[ R ₂, T ₄],

R ₁ и R ₂ – радиус-векторы точек приложения сил натяжения нити T ₂ и T ₄. Предположим, что m₂ > m₁, поэтому ускорения грузов будет направлено, как показано на рисунке. Выберем произвольное направление осей координат (например, как на рисунке) и запишем систему уравнений в проекциях.

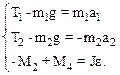(2)

При условии, что нить нерастяжима, отсутствует ее скольжение по поверхности диска, тангенциальное ускорение точек на поверхности диска а _t по модулю равно поступательному ускорению а грузов: а_t=а. Угловое ускорение диска связано с линейным ускорением грузов соотношением 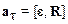; в скалярной форме 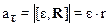. Пренебрегая массой нити приходим к выводу, что силы натяжения Т₁ и Т₂ равны по величине. Учтем также, что момент инерции диска J = mr²/2. С учетом приведенных дополнительных соотношений система (2) принимает вид:

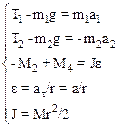
Решая полученную систему, получим

.

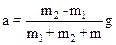После подстановки числовых значений имеем

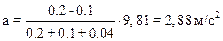
Задачи к главе 2 для самостоятельного решения

2.1. Определить, на каком расстоянии от поверхности Земли должен находиться спутник, если он вращается в плоскости экватора с периодом, равным периоду вращения Земли вокруг оси.

35870 км.

2.2. Какова должна быть продолжительность суток на Земле, чтобы тела, находящиеся на экваторе, были невесомы.

1,41 часа.

2.3. Тело массой 1 кг, закрепленное на конце невесомого стержня длиной 0,5 м, вращается в вертикальной плоскости в поле силы тяжести с постоянной частотой 0,2Гц. Вычислить разность сил, действующих на стержень в нижнем и верхнем положении.

1,6 Н.

2.4. Камень массой 0,5 кг, привязанный к веревке длиной 50 см, вращается в вертикальной плоскости. Сила натяжения веревки в нижней точке окружности равна 44 Н. На какую высоту поднимется камень, если веревка отрывается в тот момент, когда его скорость направлена вертикально вверх?

2 м.

2.5. Определить плотность планеты, если тела на ее экваторе невесомы. Период обращения планеты вокруг оси – Т = 20 ч.

r = 27, 25кг/м3.

2.6. Определить максимальную силу натяжения, которую выдерживает нить, к концу которой привязан шарик массой m = 500 г, если она разрывается, когда ее отклоняют на угол, больший 60°.

Т = 9,8Н.

2.7. На горизонтально вращающемся диске на расстоянии 1 м от вертикальной оси вращения лежит груз. При каком числе n оборотов в секунду груз начнет скользить, если коэффициент трения между грузом и диском 0,01?

n = 0,05 об/с.

2.8. Маленький шарик массы m, подвешенный на невесомой нити, отклоняют от положения равновесия на угол a = 60° и отпускают. Определить натяжение нити в начальный момент движения.

Т = mg/2.

2.9. В конусе лежит шарик. Конус начинают вращать с угловой скоростью w. На каком расстоянии от вершины конуса шарик будет находиться в состоянии равновесия? Угол раствора конуса равен 2a.

L=g/(w2cosa).

2.10. Два тела массами m₁ и m₂ находятся на стержне, по которому они могут свободно двигаться. Тела соединены нитью длиной L. Стержень вращается с угловой скоростью w относительно вертикальной оси вращения. Определить, на каком расстоянии от оси вращения установятся тела.

x₁ = m₁L/(m₁ + m₂), x₂ = m₂L/(m₁ + m₂).

2.11. Радиус планеты Марс составляет 0,53 радиуса Земли, а плотность - 0,74 плотности Земли. Найти ускорение свободного падения на Марсе.

3,86 м/с².

2.12. Найти линейную скорость и период обращения искусственного спутника Земли по круговой орбите на расстоянии Н=R от поверхности Земли, где R = 6400 км - радиус Земли. Ускорение свободного падения на поверхности Земли принять равным 9,8м/с².

v = 5, б км/с; Т = 4 ч.

2.13. Пуля попадает в шар массой М, висящий на нити длиной L, и застревает в нем. С какой максимальной скоростью может лететь пуля, чтобы нить не оборвалась? Максимальная сила натяжения, которую выдерживает нить, равна F_MAX, масса пули m₀.

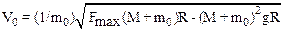
2.14. Определить угловую скорость w вращения двойной звездной системы. Массы звезд М₁ и М₂, расстояние между их центрами R. Найти также ускорения, с которыми движутся звезды.

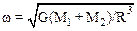; a₁ = GМ₂ / R²; a₂ = GМ₁ / R².

2.15. Найти первую космическую скорость на планете, масса которой в 3 раза, а радиус в 2 раза больше, чем у Земли. Принять первую космическую скорость на Земле равной 8×10³ м/с.

9,8×10³ м/с.

2.16. Найти момент инерции: а) тонкого однородного стержня относительно оси, перпендикулярной к стержню и проходящей через его конец, если масса стержня m и длина L; б) тонкой однородной прямоугольной пластинки относительно оси, проходящей через одну из вершин пластинки перпендикулярно к ее плоскости, если стороны пластинки раны a и b, а ее масса равна m.

а) I = mL²/3; б) I = m(a²+b²)/3.

2.17. Тонкая однородная пластинка массы m=0,60 кг имеет форму равнобедренного прямоугольного треугольника. Найти ее момент инерции относительно оси, совпадающей с одним из катетов, длина которого а=200 мм.

I=ma²/6=4,0 г·м².

2.18. Вычислить момент инерции: а) медного однородного диска относительно оси симметрии, перпендикулярной к плоскости диска, если его толщина b=2,0 мм и радиус R=100 мм; б) однородного сплошного конуса относительно его оси симметрии, если масса конуса m и радиус его основания R.

а) I = πρbR⁴/2=2,8 г·м²; б) I = 0,3mR².

2.19. Найти момент инерции тонкого проволочного кольца радиусом R и массы m относительно оси, совпадающей с его диаметром.

I=mR²/2.

2.20. Однородный диск радиуса R имеет круглый вырез (рис. 1). Масса оставшейся части диска равна m. Найти момент инерции такого диска относительно оси, перпендикулярной к плоскости диска и проходящей: а) через точку О, б) через его центр масс.

а) I_O = (13/24)mR²; б) I_C=(37/72)mR².

2.21. На ступенчатый блок (рис. 2) намотаны в противоположных направлениях две нити. На конец одной нити действуют постоянной силой F, а к концу другой нити прикреплен груз массы m. Известны радиусы R₁ и R₂ блока и его момент инерции I относительно оси вращения. Трения нет. Найти угловое ускорение блока.

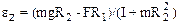
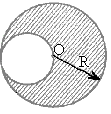Рис 1.

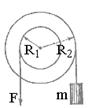Рис. 2

2.22. Человек массой m₁ стоит на краю горизонтального однородного диска массой m₂ и радиусом R, который может свободно вращаться вокруг неподвижной вертикальной оси, проходящей через его центр. В некоторый момент человек начал двигаться по краю диска, совершил перемещение на угол 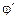относительно диска и остановился. Пренебрегая размерами человека, найти угол, на который повернулся диск к моменту остановки человека.

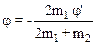
2.23. Два горизонтальных диска свободно вращаются вокруг вертикальной оси, проходящей через их центры. Моменты инерции дисков относительно этой оси равны I₁ и I₂, а угловые скорости – w₁ и w₂. После падения верхнего диска на нижний оба диска благодаря трению между ними начали через некоторое время вращаться как единое целое. Найти: а) установившуюся угловую скорость вращения дисков; б) работу, которую совершили при этом силы трения.

а) ω=(I₁ω₁+I₂ω₂)/(I₁+I₂),

б) А = - [I₁I₂/2(I₁+I₂)](ω₁ -ω₂)².

2.24. На горизонтальную ось насажены маховик и легкий шкив радиусом R=5см. На шкив намотан шнур, к которому привязан груз массой m=0,4кг. Опускаясь равноускоренно, груз прошел путь s=1,8м за время t=3с. Определить момент инерции J маховика. Массу шкива считать пренебрежимо малой.

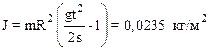
2.25. Вал массой m=100кг и радиусом R=5см вращался с частотой n=8c^-1. К цилиндрической поверхности вала прижали тормозную колодку с силой F=40Н, под действием которой вал остановился через t=10с. Определить коэффициент трения f.

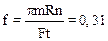
2.26. На цилиндр намотана тонкая гибкая нерастяжимая лента, массой которой по сравнению с массой цилиндра можно пренебречь. Свободный конец ленты прикрепили к кронштейну и предоставили цилиндру опускаться под действием силы тяжести. Определить линейное ускорение а оси цилиндра, если цилиндр: 1) сплошной; 2) полый тонкостенный.

1) a=2g/3; 2) a=g/2.

2.27. Человек стоит на скамье Жуковского и ловит рукой мяч массой m=0.4кг, летящий в горизонтальном направлении со скоростью V=20м/с. Траектория мяча проходит на расстоянии r=0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью w начнет вращаться скамья Жуковского с человеком, поймавшим мяч, если суммарный момент инерции J человека и скамьи равен 6кг·м².

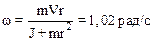
2.28. На краю горизонтальной платформы, имеющий форму диска радиусом R=2м, стоит человек массой m₁=80кг. Масса m₂ платформы равна 240кг. Платформа может вращаться вокруг вертикальной оси, проходящий через ее центр. Пренебрегая трением, найти, с какой угловой скоростью w будет вращаться платформа, если человек будет идти вдоль ее края со скоростью V=2м/с относительно платформы.

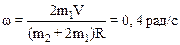
2.29.В центре скамьи Жуковского стоит человек и держит в руках стержень длиной L=2,4 м и массой m=8 кг, расположенный вертикально по оси вращения скамьи. Скамья с человеком вращается с частотой n₁=1 с^-1. С какой частотой n₂ будет вращаться скамья с человеком, если он повернет стержень в горизонтальное положение? Суммарный момент инерции J человека и скамьи равен 6 кг·м².

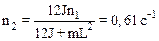
2.30. Чему равен момент инерции тонкого прямого стержня длиной 0,5 м и массой 0,2 кг относительно оси, перпендикулярной к его длине и проходящей через точку стержня, которая удалена на 0,15 м от одного из его концов?

6·10^-2 кг·м².

2.31. На барабан радиусом R=10 см намотана нить, к концу которой привязан груз массой m= 0,50 кг. Найти момент инерции барабана, если груз опускается с ускорением а =1,0 м/с².

I=mR²(g- a)/ a =4,4·10^-2 кг·м².

2.32. Через блок, масса которого m=100 г, перекинута тон­кая гибкая нерастяжимая нить, к концам которой подвешены два груза массами m₁ = 200г и m₂=300 г. Грузы удерживаются в неподвижном положении. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Чему равно угловое ускорение блока, если его радиус 10 см? Трением пренебречь.

a =(m₂-m₁)g/(m₁+m₂+m/2)=1,8 м/с²; ε=(m₂-m₁)g/(m₁+m₂+m/2)R=18 с^-2.

2.33. Из колодца с помощью ворота поднималось ведро с водой массой m=10 кг. В момент, когда ведро находилось на высоте h=5,0 м от поверхности воды, рукоятка освободилась, и ведро стало двигаться вниз. Определить линейную скорость рукоятки в момент удара ведра о поверхность воды в колодце, если радиус рукоятки R=30 см, радиус вала ворота r =10 см, его масса m₁=20 кг. Трением и массой троса, на котором подвешено ведро, пренебречь.

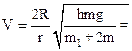21 м/с.

2.34. Маховик массой m₁=l,0 кг укреплен на шкиве радиусом r=5,0 см и массой m₂=200 г, который приводится во вращение с помощью опускающейся гири массой m₃=500 г, привя­занной к концу намотанной на шкив веревки. Через какое время скорость маховика достигнет n=5,0 об/с? Считать, что вся масса маховика распределена по его ободу радиусом R=40 см.

Глава 3. Статика

· Статика – это раздел механики, посвященный изучению условий равновесия механической системы, а так же отдельного тела.

Пусть тело в начальный момент времени покоится, т. е. его начальная линейная скорость V ₀ и начальная угловая скорость w ₀ равны нулю. Условия, при которых тело и в последующие моменты времени будет находиться в равновесии (в покое), следуют из второго закона Ньютона и уравнения моментов:

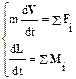
Действительно, V = V ₀=0 если d V/ dt= a =0 и поступательное движение не начнется. Аналогично момент импульса L = L ₀ останется равным нулю при отсутствии углового ускорения. Эти условия выполнены, если равнодействующая приложенных сил равна нулю и суммарный момент сил равен нулю:

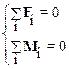
Уравнения (3.2) называются условиями равновесия механической системы (тела). Для материальной точки в качестве условий равновесия могут выступать первое уравнение системы. Система (3.2) двух векторных уравнения соответствуют следующей системе шести скалярных уравнений для проекций сил и моментов сил, действующих на материальную систему:

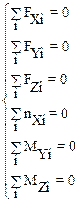
При исследовании равновесия положение осей X, Y, Z можно выбрать произвольно. Удобно провести их через центр масс тела.

· Центроммасс (центроминерции) системы называют воображаемую точку, радиус – вектор которой определяется следующим образом:

,

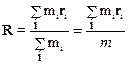здесь m_i и r _i – масса и радиус-вектор i-ой частицы системы (тела) в некоторой системе отсчета, 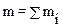– масса системы.

Дифференцируя (3.4) легко получить, что импульс Р системы равен произведению ее массы на скорость V _c движения центра масс:

.

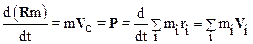Используя соотношение (3.5) и уравнение второго закона Ньютона d P /dt= F ^внеш запишем

.

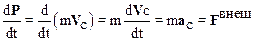Таким образом, приходим к теоремео движении центра масс системы:

· центр масс системы движется, как материальная точка с массой равной массе системы, к которой приложена равнодействующая сил.

Уравнение для моментов 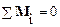может быть написано для произвольного полюса. Можно показать, что при условии 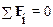величина результирующего момента сил не зависит от выбора полюса.

Найдем суммарный момент сил тяжести, действующих на все частицы системы (тела), относительно произвольной точки О:

,

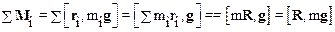где 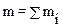– масса тела, R -радиус - вектор центра масс тела. Таким образом, момент сил тяжести частиц тела относительно произвольной точки О равен моменту силы тяжести тела m g, приложенной к центру масс тела. Из формулы (3.7) следует, что суммарный момент сил тяжести относительно центра масс тела равен нулю (так как радиус-вектор центра масс R = 0).

Глава 4. Работа силы. Мощность

· Элементарнойработой dA силы F на элементарном перемещении d S называют скалярную физическую величину, равную скалярному произведению вектора силы F и вектора перемещения d S:

,

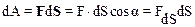здесь через F_dS обозначена проекция вектора силы на направление перемещения d S.

В общем случае, когда материальная точка под действием переменной силы F движется по некоторой криволинейной траектории L, работа силы равна

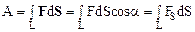
Это соотношение получено предельным переходом в сумме

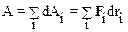
элементарных работ dA_i, совершаемых силой на каждом из элементарных перемещений d S _i вдоль трактории L:

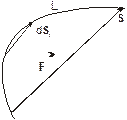
Рис. 4.1. К вычислению работы силы

· Работапостояннойсилы F на перемещении S, как следует из (4.2) равна скалярному произведению вектора силы F и перемещения S:

,

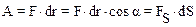где a – угол между векторами F и S, F– проекция вектора силы на направление вектора перемещения.

Если зависимость проекции вектора силы на направление перемещения представлена графически (см. рис. 4.2), то работу силы можно определить как площадь криволинейной трапеции.

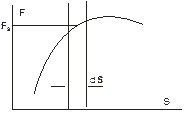
Рис. 4.2. Вычисление работы переменной силы

Наконец, соотношение (4.2) может быть записано для случая действия нескольких сил F _i. Пусть равнодействующая R равна:

,

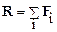тогда:

.

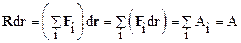Последние соотношения выражают следующие утверждения:

· работаравнодействующей силы равна алгебраической сумме работ, совершенных всеми ее составляющими.

Для нахождения работы часто удобно пользоваться следующим правилом:

,

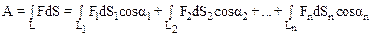где L=L₁+L₂+L₃+…+L_n:

· работа, совершенная при перемещении вдоль некоторой траектории, равна сумме работ, совершенных на отдельных участках этой траектории.

Скорость совершения работы во времени характеризует мощность.

· Средняямощность, развиваемая некоторой силой – это физическая величина, равная отношению работы силы A к промежутку времени, в течение которого эта работа была совершена:

.

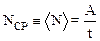· Мгновеннаямощность – мощность, затрачиваемая (выделяемая) в данный момент времени.

· Мгновеннаямощность – определяется как предел средней мощности (4.6) при условии, что промежуток времени t стремится к нулю. Это позволяет определить мощность как первую производную работы по времени:

.

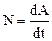Мощность, сила и скорость движения связаны между собой следующим соотношением:

.

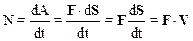Единицей измерения работы в системе СИ является джоуль (Дж). Один джоуль равен работе, совершаемой постоянной силой в 1Н на перемещении в 1м при условии, что векторы силы и перемещения сонаправлены: 1Дж = 1Н·1м. Единица измерения мощности – ватт (Вт). Один ватт равен мощности, при которой за время 1с совершается работа, равная 1Дж.

4.1. Консервативные и неконсервативные силы

в механике

Все силы в механике делятся на консервативные и неконсервативные. Такое деление связано с понятием "потенциальная энергия", которое рассматривается далее. В связи с этим, консервативные силы являются потенциальными, а неконсервативные – не потенциальными.

· Консервативнымисилами называют силы, работа которых не зависит от формы траектории, а только от начального и конечного положения движущейся материальной точки, к которой они приложены.

Консервативные силы зависят от взаимного расположения материальных точек (тел) системы, т. е. от ее конфигурации, а также от положения системы во внешних силовых полях. Отметим сразу, что в механике рассматриваются следующие консервативные силы: сила всемирного тяготения, сила тяжести и упругости. К консервативным силам относят также силу Кулона, описывающую взаимодействие заряженных частиц.

· Все силы, которые не являются консервативными, например, диссипативные и гироскопические силы, относят к неконсервативным силам.

· Диссипативными [4] силами называют силы, полная работа которых в замкнутой системе всегда отрицательна.

Диссипативные силы зависят не только от взаимного расположения взаимодействующих тел, но и от их относительной скорости. К ним, например, относятся сила трения скольжения, сила сопротивления движению в жидкой или газовой среде. Направление диссипативных сил всегда противоположно направлению относительной скорости взаимодействующих тел. В разделе будет показано, что, в самом общем случае, механическая энергия системы может не сохраняться. Одна из причин этого заключается в действии диссипативных сил, которые приводят к частичному или полному переходу механической энергии во внутреннюю энергию.

· Гироскопическимисилами называют силы, которые действуют перпендикулярно скорости движения частицы (тела) и зависят от ее величины.

Гироскопической силой является, например, сила Лоренца 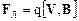. В силу специфической направленности гироскопических сил они не совершают работы, не изменяют модуль скорости, а только изменяют ее направление. Действительно, вектор векторного произведения 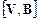перпендикулярен V, поэтому:

.

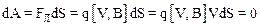Возвращаясь к изучению свойств консервативных сил, докажем их основное свойство:

· работа консервативных сил по любой замкнутой траектории равна нулю.

Пусть материальная точка (система) из положения 1 перешла в положение 2 по траектории 132 (см. рис. 4.3).

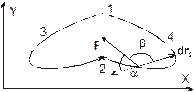
Рис. 4.3. Свойство консервативных сил

При этом консервативной силой F, действующей на нее, была совершена работа 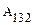. Предположим, что при переходе в положение 2 по траектории 142, работа равна 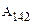. По определению консервативных сил имеем 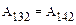. Заметим теперь, что работы, совершенные на участках 142 (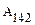) и 241 (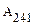) отличаются знаком: т. е. 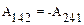. Это связано с тем, что на каждом элементарном участке траектории 241 угол b между вектором F и вектором перемещения d r ₂=d r ₂₄₁ является дополнительным к углу a между векторами F и вектору d r ₁=d r ₁₄₂, который противоположен вектору d r ₂. По этой причине знак функции косинуса (и работы) в выражении (4.1) изменяется на противоположный.

На основании (4.5) заключаем, что работа консервативных сил по замкнутой траектории 13241 А₁₃₂₄₁ равна сумме работ А₁₃₂ и А₂₄₁ вдоль траекторий 132 и 241, соответственно:

А₁₃₂₄₁= А₁₃₂+ А₂₄₁= А₁₃₂–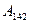=0.

Сформулированное утверждение доказано.

4.1.1. Работасилы тяжести

Вычислим работу силы тяжести m g, совершаемую при перемещении материальной точки (тела) массой m из положения 1 в положение 2. Используя формулу (4.2) получим,

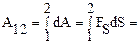
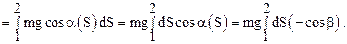
Из чертежа видно, что dScosb=dh; тогда выражение для А₁₂ можно преобразовать так:

.

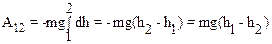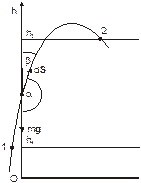
Рис. 4.4 К вычислению работы силы тяжести

Полученное выражение для А₁₂ показывает, что независимо от вида траектории работа по перемещению материальной точки (тела) в поле тяжести зависит только от ее начальной и конечной высоты:

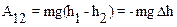
4.1.2. Работасилы всемирного тяготения

Вычислим работу, совершаемую силой всемирного тяготения со стороны тела массой М при перемещении тела массой m из положения, характеризуемого радиус-вектором r ₁ в положение с радиус-вектором r ₂ (см. рис. 4.5).

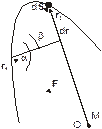
Рис. 4.5. Вычисление работы силы тяготения и силы упругости. Тяготеющая масса М расположена в точке О

Гравитационное поле является центральным, поскольку сила тяготения действует вдоль линии соединяющей материальную точку m (или центр масс этого тела) с центром О поля тяготения. По определению работы (4.2) имеем:

,

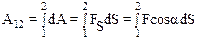где сила F определяется законом (2.12).

Из рисунка видно, что dScosa=dr, поэтому dA=F(r)dr, и для А₁₂ имеем:

.

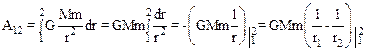Полученное выражение не содержит сведений о траектории движения тела, и можно утверждать, что работа центральной силы зависит только от начального и конечного расстояния r₁ и r₂ движущейся точки до силового центра.

4.1.3. Работасилы упругости

Вывод формулы для работы силы упругости проводится аналогично выводу для силы всемирного тяготения. Эта работа равна

,

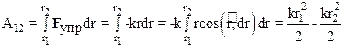Здесь r₁ и r₂ – величина абсолютной деформации тела в начальном и конечном состояниях. Эти деформации представляют собой координаты точки приложения внешней (деформирующей) силы при условии, что начало координат соответствует недеформированному состоянию тела. Как в ранее рассмотренных случаях, работа силы оказывается независимой от формы траектории точки приложения силы, и определяется только ее начальным и конечным положениями.

Глава 5. Энергия

· Энергия – это способность тела (системы) совершать работу.

Энергия служит универсальной количественной мерой движения и взаимодействия всех видов материи. Различают два вида механической энергии: потенциальную и кинетическую.

Дата добавления: 2013-12-12