Динамика поступательного движения

материальной точки (тела)

Динамика, как составная часть механики решает основную задачу механики. Собственно, задача динамики состоит в нахождении ускорения движущейся материальной точки (тела) при условии, что известны силы, действующие на нее. После этого задача об определении движения сводится к кинематическим соотношениям. Таким образом, исследование движения материальной точки состоит в совместном решении системы кинематических уравнений и уравнения второго закона Ньютона:

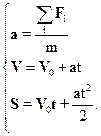
2.5.1. Импульс материальной точки

· Импульсомматериальнойточки массой m, движущейся со скоростью V называют векторную физическую величину, равную произведению массы точки на ее скорость:

.

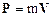Обратим внимание, что в литературе предыдущих лет широко использовался термин "количество движения", в настоящее время вместо него рекомендовано использовать термин "импульс".

Дифференцируя соотношение (2.22) по времени, получим:

.

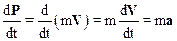Из последнего соотношения следует, что уравнение второго закона Ньютона можно записать следующим образом:

.

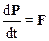Известно, что первая производная некоторой величины по времени характеризует скорость ее изменения, поэтому уравнение (2.23) читают так:

· скорость изменения импульса материальной точки равна действующей на нее силе.

Пусть на материальную точку m действует несколько постоянных сил F ₁, F ₂, … F _i. Обозначим равнодействующую этих сил через R:

,

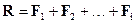и пусть Dt – время действия этих сил. Разделим этот промежуток времени на малые промежутки dt. За время dt, под действием внешних сил скорость материальной точки изменится в соответствии со вторым законом Ньютона:

.

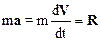Разделяя переменные в последнем соотношении 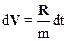, и интегрируя по времени в пределах от t1 до t2(Dt= t2- t1), получим:

.

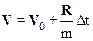Преобразуем полученное выражение к виду, определяющему изменение импульса:

.

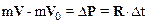В проекциях на оси координат формула (2.24) записывается так:

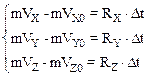
· Импульс действия силы – векторная величина, равная произведению силы F на время ее действия Dt.

Смысл соотношения (2.24) может быть выражен следующим образом:

· приращение импульса материальной точки равно импульсу действия силы

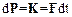или .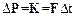

Если сила F изменяется с течением времени, то импульс действия силы К равен

,

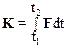где t₁ и t₂ время начала и окончания действия силы.

2.5.2. Импульс механической системы

Определение механической системы, как совокупности тел, рассматриваемых в данной задаче, позволяет считать механической системой совокупность материальных точек, материальное тело, а также совокупность материальных тел.

· Импульс Р механической системы, состоящей из N материальных точек (тел) равен векторной сумме импульсов этих точек (тел), входящих в эту систему:

.

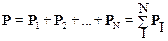Таким образом, импульс – есть величина аддитивная.

При поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по величине и направлению скорости и ускорения. Импульс Р тела, имеющего конечные размеры и массу m, движущегося поступательно со скоростью V, равен импульсу материальной точки такой же массы m, движущейся с той же скоростью:

Р=mV.

Заметим, что силы, действующие на материальную точку, всегда происходят от иных материальных точек (тел). На тела механической системы могут действовать силы со стороны тел системы, так и со стороны тел, не входящих в эту систему. Силы взаимодействия между телами системы называются внутренними; силы, действующие со стороны иных тел, называются внешними.

· Внутренние силы – это силы взаимодействия между телами механической системы.

В дальнейшем силы будут обозначаться следующим образом: f_ij – внутренняя сила, действующая на i-ое тело системы со стороны j-го тела системы, F_i – внешняя сила, действующая на i-ое тело системы.

Рассмотрим механическую систему, состоящую из N материальных точек массами m₁, m₂, …, m_N. Предположим, что на каждое из них действуют как тела самой системы, так и внешние, по отношению к ней, тела.

Запишем уравнение второго закона Ньютона для каждого из тел системы:

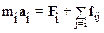, (i=1, 2, …,N).

Сложим почленно правые и левые части уравнений, в результате чего получим

.

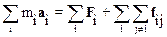Третий закон Ньютона позволяет утверждать, что сумма всех внутренних сил, действующих в системе, равна нулю. Таким образом:

.

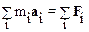Преобразуем полученное соотношение:

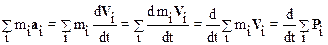
Обозначим 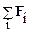через R ^ВНЕШ – равнодействующую всех внешних сил, а 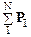как Р – импульс системы.

Уравнение (2.30) примет вид:

.

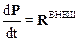Можно сделать следующие выводы.

· Скорость изменения импульса механической системы равна сумме внешних сил, действующих на эту систему.

· Уравнение (2.23), полученное для материальной точки, аналогично уравнению (2.31) справедливому для системы материальных точек и для механической системы.

Замечание.

· Импульс тела, имеющего неподвижную ось вращения, равен нулю.

Это утверждение несложно доказать в общем случае. Проиллюстрируем его примером. Вычислим импульс однородного диска, вращающегося вокруг неподвижной оси, проходящей через его центр.

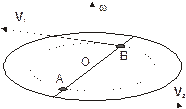
Рис. 2.15

Для этого разделим мысленно диск на элементарные части, так, чтобы массы этих частей были одинаковыми. Рассмотрим две частицы тела dm₁ и dm₂, расположенные в точках А и В диаметра на равных расстояниях и по разные стороны от центра диска (см. рис.2.15).

Линейные скорости этих частиц равны по величине, но противоположны по направлению: V ₁ = – V ₂. Суммарный импульс частиц dm₁ и dm₂ равен нулю, т. к.

dm V ₁+dm V ₂=dm (V ₁+ V ₂)=0.

Так как каждой частице на диске найдется частица ей диаметрально противоположная, то суммарный импульс диска равен нулю.

Импульс имеет большое значение при рассмотрении процессов соударения, которые будут рассматриваться далее.

· Удар– взаимодействие, протекающее в течение малого промежутка времени.

· Абсолютнонеупругимударом называется взаимодействие, в результате которого тела начинают двигаться вместе с одинаковыми скоростями. Можно говорить, что при неупругом ударе образуется составное тело с массой, равной массе сталкивающихся тел.

· Абсолютноупругимударом называется взаимодействие, в результате которого скорости тел изменяются, но суммарные импульс механическая энергия остаются неизменными.

2.5.2. Динамика движения материальной точки

по окружности

Кинематика вращательного движения материальной точки рассматривалась в пунктах 1.4-1.5. Было отмечено, что даже при равномерном движении материальной точки по окружности, ее линейная скорость непрерывно изменяется по направлению. Это происходит благодаря ускорению (см.(1.24)), называемому центростремительным а_Ц, или нормальным ускорением – а_n. Ускорение материальной точки, в соответствии со вторым законом Ньютона, сонаправлено с вектором равнодействующей приложенных сил, и равно:

.

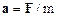Таким образом, равномерное движение по окружности материальная точка может совершать, если равнодействующая F всех сил, приложенных к ней, направлена к центру окружности. Часто силу вызывающую центростремительное ускорение называют "центростремительной силой". Этот термин, как правило, вызывает заблуждение, ориентируя на поиск специфической центростремительной силы. Такой особой – центростремительной силы в природе не существует. Центростремительное ускорение вызывает равнодействующая приложенных сил! Во избежание недоразумений и ошибок мы рекомендуем не пользоваться термином "центростремительная сила", а уравнение динамики вращательного движения материальной точки, масса которой равна m, записывать в следующем виде:

.

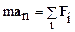Динамика движения материальной точки по окружности может быть изучена на основе общего подхода – с помощью основного закона динамики вращательного движения. Уточним некоторые определения.

· Моментсилыотносительноточки О (полюса О) – векторная физическая величина, равная векторному произведению радиус-вектора r точки приложения силы, проведенного из точки О, и вектора силы F:

.

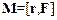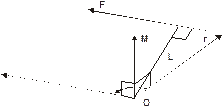
Рис. 2.16. К определению вектора момента силы.

Напомним, что векторное произведение представляет собой вектор, направление которого определяется по правилу буравчика (см. (Б.II), параграф 1.5). Абсолютная величина (модуль) вектора векторного произведения равна произведению модулей векторов–сомножителей и синуса угла между ними

.

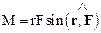Из рисунка 2.16 видно, что модуль М можно представить следующим образом:

,

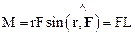где 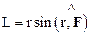– плечо силы относительно точки О.

· Плечосилы – кратчайшее расстояние от полюса О до линии действия силы, т. е. длина перпендикуляра, опущенного из полюса на линию действия силы.

· Моментсилыотносительнооси – это скалярная величина М, равная проекции на эту ось вектора момента силы М, определенного относительно точки, лежащей на этой оси:

,

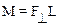где F_┴ – проекция силы F на плоскость, перпендикулярную оси Z, L – плечо силы F относительно оси Z.

В случае действия нескольких сил F _i результирующий момент равен векторной сумме моментов M _i всех сил:

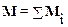или ,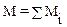

в последнем выражении берут алгебраическую сумму, в которой знак M_i зависит от знака проекции M _i на ось Z.

· Моментимпульсаматериальнойточкиотносительноточки (полюса – О) – это векторная величина, равная векторному произведению L= [ r,р ], где r – радиус-вектор материальной точки (начало которого находится в полюсе О), р – импульс точки.

· Моментинерцииматериальнойточкиотносительнооси – скалярная величина, равная произведению массы m материальной точки на квадрат расстояния r от материальной точки до оси:

.

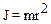Вращательное движение материальной точки описывается уравнением, которое называется основным уравнением динамики вращательного движения. Запишем уравнение второго закон Ньютона для материальной точки, движущейся по окружности радиусом r:

. (*)

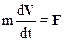Учитывая формулу Эйлера 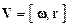, перепишем (*) следующим образом:

.

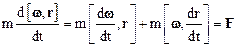Умножим справа обе части полученного уравнения векторно на радиус-вектор r материальной точки:

.

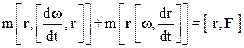Соотношение (2.35) можно упростить. Действительно, поскольку вектор 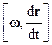параллелен вектору r, то

.

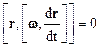Имеем:

.

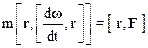Раскрывая оставшееся двойное векторное произведение(см. (1.23)):

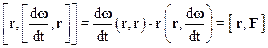
и учитывая, что векторы r иd w /dt взаимно перпендикулярны, а поэтому их скалярное произведение равно нулю, приходим к выражению:

.

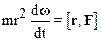Правая часть уравнения (2.36) представляет собой момент М силы F относительно полюса.Произведение mr²=J есть момент инерции материальной точки, d w /dt= e – угловое ускорение вращательного движения. Следовательно, уравнение (2.36) можно записать так:

.

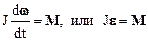Уравнения(2.37) выражает основной закон динамики вращательного движения материальной точки. Оно является не только следствием, но и полным аналогом второго закона Ньютона m a = F для случая поступательного движения материальной точки.

Заметим, что уравнение 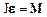получено для случая, когда полюс совпадает с центром вращения материальной точки. Если рассматривать движение материальной точки относительно оси вращения Z, то уравнение движения примет соответствующую скалярную форму:

,

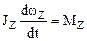где M_Z – суммарный момент сил относительно оси Z, J_Z – момент инерции относительно оси, w_Z – проекция угловой скорости на ось Z, dw_Z/dt=e – угловое ускорение.

Продифференцируем уравнение L =[ r, P ], определяющее момент импульса L материальной точки по времени:

Дата добавления: 2013-12-12