Лекция 18

Методы решения простейших дифференциальных уравнений первого порядка (с разделяющимися переменными, «однородных», линейных и сводящихся к ним).

Лекция 17.

1. Уравнения с разделяющимися переменными.

Дифференциальные уравнения вида

f₂(y)dy = f₁(x)dx (17.1)

называются уравнениями с разделяющимися переменными. Тогда любое решение у(х) этого уравнения будет удовлетворять и уравнению

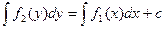, (17.2)

где с – произвольная постоянная. Если удается найти первообразные функций f₁(x) и f₂(y), выраженные в элементарных функциях, то из (17.2) можно получить конечное уравнение вида Ф (х, у) = 0, (17.3)

которое определяет решение у(х) уравнения (17.1) как неявную функцию х.

Определение 17.1. Уравнение вида (17.3) называется интегралом уравнения (17.1), а если оно определяет все решения (17.1) – общим интегралом этого уравнения.

Пример.

. Приведем уравнение к виду (17.1): , откуда 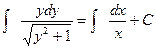. Проинтегрируем обе части равенства: 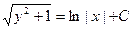. Полученное уравнение можно считать общим интегралом или решением исходного уравнения.

Если требуется найти частное решение уравнения (17.1), удовлетворяющее условию у(х₀)=у₀, достаточно подставить значения х₀ и у₀ в уравнение (17.3) и найти значение с, соответствующее начальному условию.

Пример.

Найти решение уравнения y′ ctg x + y = 2, удовлетворяющее условию у (0) = -1.

Разделим переменные: 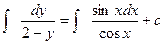, -ln | 2 – y | = -ln | cos x | - ln | c |,

2 – y = c • cos x. Подставив в это равенство х = 0 и у = -1, получим, что с = 3. Следовательно, искомое частное решение имеет вид: y = 2 – 3cos x.

2. Уравнения, приводимые к уравнениям с разделяющимися переменными.

Если требуется решить уравнение вида 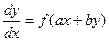, (17.4)

где а и b – постоянные числа, то с помощью замены переменной z = ax+by оно сводится к уравнению с разделяющимися переменными:

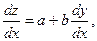
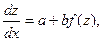
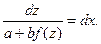
Пример.

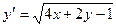. Замена: z = 4 x + 2 y – 1, тогда 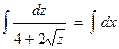+ с. Вычислим интеграл в левой части равенства: замена 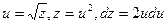приводит к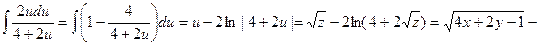

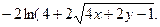Проинтегрировав теперь правую часть равенства, получим общий интеграл: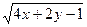

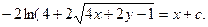
3.Однородные уравнения.

К уравнениям с разделяющимися переменными приводятся и так называемые однородные дифференциальные уравнения первого порядка, имеющие вид:

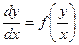. (17.5)

Действительно, замена 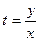или y = xt приводит к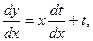

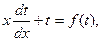
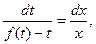
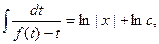
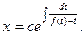
Еще одной формой однородного уравнения является уравнение

M(x,y) dx + N(x,y) dy = 0, (17.6)

если М(х,у) и N(x,y) – однородные функции одинаковой степени однородности. При этом .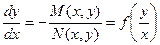

Пример.

y ² + x ² y′ = xyy′. Преобразуем уравнение к виду (17.5): y′ (xy – x ²) = y ², ,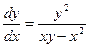

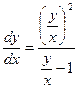. После замены y = xt получим: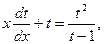

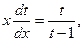
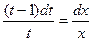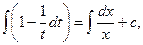, t – ln | t | = ln | x | + ln | C|, , .

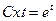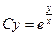В однородные можно преобразовать и уравнения вида

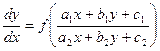(17.7)

с помощью замены Х = х – х₁, Y = y – y₁, где х₁, у₁ – решение системы уравнений

a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0.

(C геометрической точки зрения производится перенос начала координат в точку пересечения прямых a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0). Тогда, поскольку 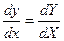, в новых переменных уравнение примет вид:

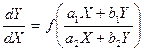или 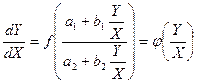- однородное уравнение.

Пример.

(у + 2) dx = (2 x + y – 4) dy. Запишем уравнение в виде 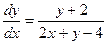. Решением системы у + 2 = 0, 2 х + у ­ – 4 = 0 будут х₁ = 3, у₁ = -2. В новых переменных Х = х – 3,

Y = y + 2 получим однородное уравнение 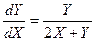, которое можно решить с помощью обычной замены Y = Xt. Тогда , ,

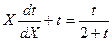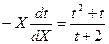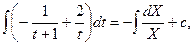
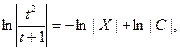, и после обратной замены общий интеграл выглядит так: 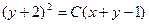. Заметим, в это общее решение входит при С =0 и частное решение у = 1 – х, которое могло быть потеряно при делении на у + х –1.

4. Линейные уравнения.

Линейным дифференциальным уравнением первого порядка называется уравнение вида

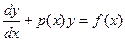, (17.8)

линейное относительно неизвестной функции у(х) и ее производной. При этом будем предполагать, что р(х) и f(x) непрерывны.

В случае, когда f(x) ≡ 0, уравнение (17.8) называется однородным. Такое уравнение является уравнением с разделяющимися переменными:

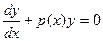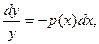
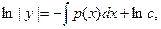
, откуда 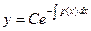.(17.9)

При делении на у могло быть потеряно решение у = 0, но оно входит в общее решение при С = 0.

Для решения неоднородного уравнения (17.8) применим метод вариации постоянной. Предположим, что общее решение уравнения (17.8) имеет форму (17.9), в которой С – не постоянная, а неизвестная функция аргумента х: 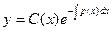. Тогда

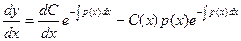. Подставив эти выражения в уравнение (17.8), получим: 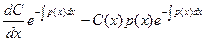+ р(х) 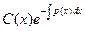= f(x), откуда

(17.10)

Замечание. При решении конкретных задач удобнее не использовать в готовом виде формулу (17.10), а проводить все указанные преобразования последовательно.

Пример.

Найдем общее решение уравнения у′ = 2 х (х ² + y). Представим уравнение в виде:

y′ - 2 xy = 2 x³ и решим соответствующее однородное уравнение: y′ - 2 xy = 0.

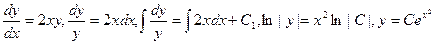. Применим метод вариации постоянных: пусть решение неоднородного уравнения имеет вид:

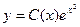, тогда . Подставим полученные выражения в уравнение: . Следовательно, ,

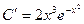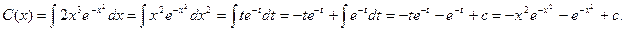При этом общее решение исходного уравнения .

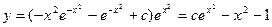К линейным уравнениям можно свести с помощью замены некоторые другие дифференциальные уравнения, например, уравнение Бернулли:

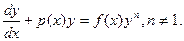(17.11)

Разделив на у^п, получим: , а замена z = y ^{1- n}, приводит к линейному уравнению относительно z:

.

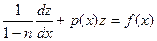Пример.

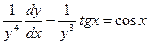. Сделаем замену:

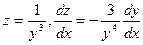. Относительно z уравнение стало линейным: .

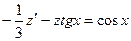Решим однородное уравнение: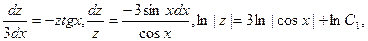

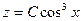. Применим метод вариации постоянных:

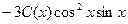. Подставим эти результаты в неоднородное уравнение:

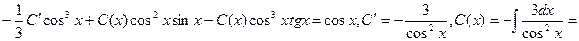
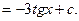Окончательно получаем: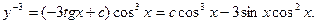

Дополним это общее решение частным решением у = 0, потерянным при делении на у ⁴.

Дата добавления: 2013-12-12