Свойства векторного произведения. Векторное произведение векторов, смешанное произведение векторов, основные свойства

Векторное произведение векторов, смешанное произведение векторов, основные свойства. Условия ортогональности, коллинеарности, компланарности векторов.

Лекция 6

Цель: Изучить векторное и смешанное произведение векторов, их свойства, методы вычисления, условия ортогональности, компланарности и коллинеарности векторов.

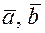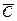Определение. Векторным произведением двух векторов , обозначают называется вектор удовлетворяющий трем условиям:

1) Модуль вектора равен площади параллелограмма, построенного на этих векторах

(6.1)

2) Вектор ортогонален перемножаемым векторам: 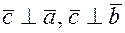т.е. ортогонален плоскости построенного на этих векторах параллелограмма

3) составляют правую тройку векторов (рис.6.1).

Рис. 6.1

1) (антикоммутативность)

Свойство следует из перемены ориентации векторов;

2) Скалярный множитель можно вынести за скобку ;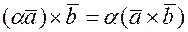

3) (дистрибутивность);

4) Векторный квадрат равен нуль-вектору:

(6.2)

Свойство непосредственно вытекает из определения векторного произведения

Теорема. Чтобы векторы и 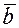были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулю.

(6.3)

Доказательство. Докажем, что есливекторы коллинеарны, то их векторное произведение равно нулю. Действительно, т.к. векторы и 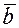коллинеарны, значит, угол 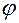между ними составляет либо . Тогда , т.е. длина вектора, полученного в результате перемножения коллинеарных векторов, равна нулю, это возможно только у нулевого вектора.

Докажем теперь, что если векторное произведение равно нулю, то векторы коллинеарны. Пусть оба вектора и 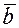ненулевые (в противном случае доказательство тривиально), тогда и , поэтому 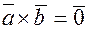только в том случае, если , т.е. векторы 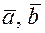должны быть коллинеарны.

Теорема. В ортонормированном базисе декартовой прямоугольной системы координат 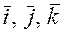компоненты векторного произведения могут быть вычислены по формуле:

(6.4)

где , .

Доказательство. Поскольку 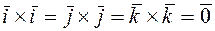и

, , , , ,

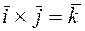тогда

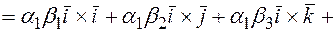
=(учитывая выше записанные равенства, упрощаем полученное выражение)

.

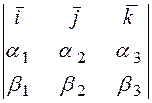Вместо 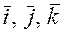можно взять любой ортонормированный базис.

Теорема (о коллинеарных векторах). Если два вектора коллинеарны, то их координаты пропорциональны:

(6.5)

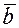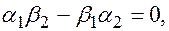
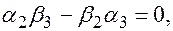
Доказательство. Пусть и , т.к. вектор коллинеарен, тогда , согласно предыдущей теореме, выполняются равенства , получаем пропорцию .

Дата добавления: 2013-12-11