Лекция 13. 2. Решение ЛОДУ n –го порядка с постоянными коэффициентами.

2. Решение ЛОДУ n –го порядка с постоянными коэффициентами.

Задача нахождения общего решения ЛОДУ n-го порядка 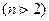с постоянными коэффициентами

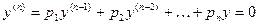(18)

Где 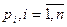- числа,решается аналогично случаю уравнения второго порядка с постоянными коэффициентами.

Покажем как это делается.

Частные решения уравнения (18) будем также искать в виде 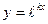,где k – const.Характеристическим для этого уравнения является алгебраическое уравнение n-го порядка 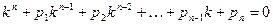(19)

Последнее уравнение имеет, как известно, n корней (в их числе могут быть и комплексные).Обозначим их через 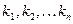.Кстати, не все из корней уравнения (19) обязаны быть различными так, например, уравнение 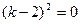имеет два одинаковых корня k=2.В этом случае говорят, что корень один k=2 и имеет кратность mk= 2.

Если mk=1,то такой корень называют простым.

Вариант 1. Если все корни уравнения (19) действительны и просты, то функции

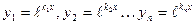являются частными решениями уравнения (18) и образуют фундаментальную систему решений (линейно независимых). Поэтому общее решение уравнения (18) запишется в виде

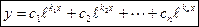
Пример: Решить

Характеристическое уравнение примет вид 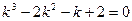и имеет корни 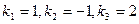.Следовательно 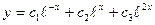- общее решение нашего уравнения.

Вариант 2. Все корни характеристического уравнения действительные, но не все простые (есть корни имеющие кратность 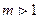) Тогда каждому простому корню k соответствует одно частное решение вида 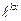,а каждому корню k кратности 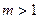соответствует m частных решений .

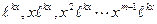Пример: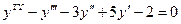

Характеристическое уравнение 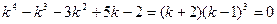имеет корни 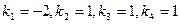, следовательно

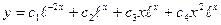- общее решение.

Вариант 3. Среди корней уравнения (19) есть комплексные корни. Тогда каждой паре 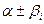простых комплексно сопряженных корней соответствует два частных решения

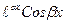и 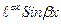,а каждой паре 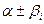корней кратности 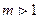соответствуют 2m частных решений вида

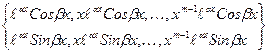
Эти решения, как можно доказать, образуют фундаментальную систему решений.

Пример: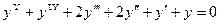

Характеристическое уравнение 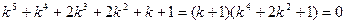имеет корни 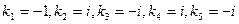, следовательно

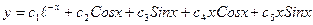- общее решение уравнения.

Дата добавления: 2013-12-12