Организационные структуры управления

ВВЕДЕНИЕ

Вопросы

1. Выделите направленность методов менеджмента и их теоретические основы.
2. Дайте характеристику общенаучным методам менеджмента.
3. Назовите компоненты административных методов управления.
4. Приведите описание регуляторов административных методов.

Основной задачей радиотехники является передача сообщения на расстояние. Расстояние разделяет отправителя и адресата, датчик команд и исполнительное устройство, исследуемый процесс и измерительный механизм, источник космического радиоизлучения и регистрирующий прибор радиотелескопа, различные блоки ЭВМ — словом, источник и потребитель информации.

Расстояние, на которое передается сообщение, может быть очень незначительным (передача команд в ЭВМ от одного блока к другому) или огромным (межконтинентальная или космическая связь). Передача сообщений осуществляется с помощью проводных, кабельных, волноводных линий или в свободном пространстве. Естественно, что для передачи сигналов целесообразно использовать те физические процессы, которые имеют свойство перемещаться. К числу таких процессов относятся применяемые в радиотехнике электромагнитные колебания — радиоволны.

Любой физический процесс, используемый в качестве агента (посредника, переносчика) для передачи информации, должен обладать свойством принимать всю совокупность состояний, по которым можно было бы однозначно установить соответствующее состояние объекта или процесса, являющегося источником информации. Для этого радиоволны подвергают модуляции. Процесс модуляции заключается в том, что высокочастотное колебание, способное распространяться на большие расстояния, наделяется признаками, характеризующими полезное сообщение. Таким образом, это колебание используется как переносчик сообщения, подлежащего передаче.

Выбор длины волны излучаемого колебания весьма существен для обеспечения устойчивой и надежной связи. Выбор того или иного диапазона волндля каждой конкретной системы связи определяется следующими факторами:

- особенностью распространения электромагнитных волн данного диапазона;

- характером помех в данном диапазоне;

- характером сообщения (шириной спектра);

- габаритными размерами антенной системы, необходимыми для осуществления направленного излучения.

Практически для использования пригодны те участки диапазона, в которых обеспечиваются благоприятные условия распространения радиоволн и в приемлемой степени удовлетворяются остальные перечисленные условия. Для современной радиотехники характерны интенсивное изучение малоисследованных диапазонов волн и стремление к расширению диапазона используемых волн в сторону как весьма длинных, так и коротких, вплоть до световых. Последнее не должно казаться странным, так как радиоволны и световые волны имеют одинаковую природу (электромагнитные волны).

В процессе передачи и приема сообщений сигналы подвергаются различным преобразованиям. Некоторые из этих преобразований являются типовыми, обязательными для большинства радиотехнических систем независимо от их назначения, а также от характера передаваемых сообщений. Перечислим эти фундаментальные процессы и попутно отметим их основные черты применительно к обобщенной схеме радиотехнического канала, представленной на рис. 1.1.

Преобразование исходного сообщения в электрический сигнал и кодирование. При передаче речи и музыки такое преобразование осуществляется с помощью микрофона, при передаче изображений (телевидение) — с помощью передающих трубок (например, суперортикона). При передаче письменного сообщения (радиотелеграфия) сначала осуществляют кодирование, заключающееся в том, что каждая буква текста заменяется комбинацией стандартных символов (например, точек, тире и пауз в коде Морзе), которые затем преобразуют в стандартные электрические сигналы (например, импульсы разной длительности или разной полярности).

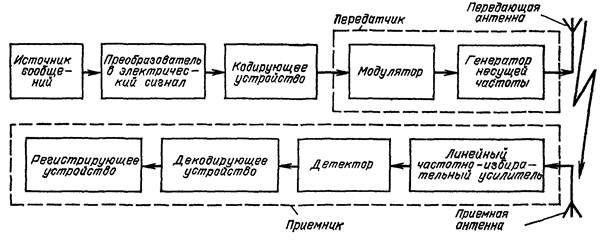
Рис. 1.1. Обобщенная схема радиотехнического канала связи

Следует отметить, что схема на рис. 1.1 соответствует введению информации «в начале» канала связи, т. е. непосредственно в передатчике. Несколько иначе обстоит дело, например, в радиолокационном канале, где информация о цели (дальность, высота, скорость и т. д.) получается в результате приема радиоволны, отраженной от цели.

Генерация высокочастотных колебаний. Высокочастотный генератор является источником колебаний несущей частоты. В зависимости от назначения радиоканала связи мощность колебаний изменяется от тысячных долей до миллионов ватт. Естественно, что конструктивные формы и размеры этих генераторов различны — от простейшего малогабаритного элемента до грандиозного технического сооружения.

Основными характеристиками высокочастотного генератора являются частота и диапазонность (возможность быстрой перестройки с одной рабочей частоты на другую), мощность и КПД. Особенно важное значение для радиотехники имеет стабильность частоты колебаний. Условия распространения радиоволн и широкий спектр частот диктуют применение очень высоких несущих частот. Условия же обработки сигналов на фоне помех и необходимость ослабления взаимных помех между различными радиоканалами заставляют добиваться максимально возможного уменьшения абсолютных изменений частоты. Это приводит к чрезвычайно жестким требованиям к относительной стабильности частоты.

Управление колебаниями (модуляция). Процесс модуляции заключается в изменении одного или нескольких параметров высокочастотного колебания по закону передаваемого сообщения. Частоты модулирующего сигнала, как правило, малы по сравнению с несущей частотой генератора. Для осуществления модуляции используются различные приемы, обычно основанные на изменении потенциала электродов электронных приборов, входящих в радиопередающее устройство. Основная характеристика процесса модуляции — степень соответствия между изменением параметра высокочастотного колебания и модулирующим сигналом.

Усиление слабых сигналов в приемнике. Антенна приемника улавливает ничтожную долю энергии, излучаемой антенной передатчика. В зависимости от расстояния между передающей к приемной станциями, от степени направленности излучения антенн и условий распространения радиоволн мощность на входе приемника 10^-10 — 10^-14 Вт. На выходе же приемника для надежной регистрации сигнала требуется мощность порядка единиц ватт и более. Отсюда следует, что усиление в приемнике должно достигать 10⁷— 10¹⁴ по мощности или 10⁴—10⁷ по напряжению.

В современных приемниках уверенная регистрация сигнала обеспечивается при напряжениях на входе порядка 1 мкВ. Решение этой сложной задачи оказывается возможным благодаря достижениям современной электроники. Большую роль играют также специальные методы построения схем приемников, обеспечивающие большое усиление при сохранении устойчивости работы приемника.

Проблема усиления в приемнике неотделима от проблемы выделения сигнала на фоне помех. Поэтому одним из основных параметров приемника является избирательность, под которой подразумевается способность выделять полезные сигналы из совокупности сигнала и посторонних воздействий (помех), отличающихся от сигнала частотой. Частотная избирательность осуществляется с помощью резонансных колебательных цепей.

Выделение сообщения из высокочастотного колебания (детектирование и декодирование). Детектирование является процессом, обратным модуляции. В результате детектирования должно быть получено напряжение (ток), изменяющееся во времени так же, как изменяется один из параметров (амплитуда, частота или фаза) модулированного колебания, т. е. должно быть восстановлено передаваемое сообщение. Детектор, как правило, включается на выходе приемника, следовательно, к нему подводится модулированное колебание, уже усиленное предыдущими ступенями приемника. Основное требование к детектору — точное воспроизведение формы сигнала. После детектирования осуществляется декодирование сигнала, т. е. процесс, обратный кодированию. В ряде радиотехнических каналов кодирование и декодирование не используются.

Помимо перечисленных процессов, так или иначе связанных с преобразованием частотных спектров, в радиотехнических устройствах широкое применение находит усиление колебаний без трансформации частоты, осуществляемое в различных усилителях. К таким усилителям относятся:

- низкочастотные усилители управляющих сигналов, используемые перед модулятором передатчика, а также на выходе приемника;

- усилители коротких импульсов, применяемые в телевизионной и радиолокационной технике, а также в импульсных системах радиосвязи;

- высокочастотные усилители большой мощности, используемые в радиопередающих устройствах;

- высокочастотные усилители слабых сигналов, применяемые в радиоприемных и измерительных устройствах.

Кроме упомянутых процессов, присущих, как уже отмечалось, любому радиотехническому каналу, в ряде специальных случаев широко применяются другие процессы: умножение и деление частоты, генерация коротких импульсов, различные виды импульсной модуляции и т. д.

В соответствии с основной задачей радиотехники в курсе РТЦ и С изучаются следующие основные вопросы.

1. Свойства разнообразных сигналов и помех, а также принципы их математического описания.

2. Свойства физических систем, выполняющих роль радиотехнических цепей.

3. Методы анализа преобразований сигналов в радиотехнических цепях, способы построения основных видов цепей.

1. РАДИОТЕХНИЧЕСКИЕ СИГНАЛЫ

1.1. Классификация РТ сигналов

С информационной точки зрения сигналы можно разделить на детерминированные и случайные.

Детерминированным называют любой сигнал, мгновенное значение которого в любой момент времени можно предсказать с вероятностью единица. Примерами детерминированных сигналов могут служить импульсы или пачки импульсов, форма, амплитуда и положение во времени которых известны, а также непрерывный сигнал с заданными амплитудными и фазовыми соотношениями внутри его спектра.

К случайным относят сигналы, мгновенные значения которых заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью, меньшей единицы. Такими сигналами являются, например, электрическое напряжение, соответствующее речи, музыке, последовательности знаков телеграфного кода при передаче неповторяющегося текста. К случайным сигналам относится также последовательность радиоимпульсов на входе радиолокационного приемника, когда амплитуды импульсов и фазы их высокочастотного заполнения флуктуируют из-за изменения условий распространения, положения цели и некоторых других причин. Можно привести большое число других примеров случайных сигналов. По существу, любой сигнал, несущий в себе информацию, должен рассматриваться как случайный.

Перечисленные выше детерминированные сигналы, «полностью известные», информации уже не содержат. В дальнейшем такие сигналы часто будут обозначаться термином колебание.

Наряду с полезными случайными сигналами в теории и практике приходится иметь дело со случайными помехами — шумами. Уровень шумов является основным фактором, ограничивающим скорость передачи информации при заданном сигнале. Поэтому изучение случайных сигналов неотделимо от изучения шумов. Полезные случайные сигналы, а также помехи часто объединяют термином случайные колебания или случайные процессы.

Детерминированные сигналы могут быть подразделены на периодические и непериодические. Периодическим называется любой детерминированный сигнал, для которого выполняется условие S(t) = S(t + kT), где период Т является конечным отрезком времени, а k – любое целое число. Непериодическим детерминированным сигналом называется любой детерминированный сигнал, для которого не выполняется условие S(t) = S(t + kT).

Дальнейшее подразделение сигналов можно связать с их природой: можно говорить о сигнале как о физическом процессе или как о закодированных, например в двоичный код, числах. В первом случае под сигналом понимают какую-либо изменяющуюся во времени электрическую величину (напряжение, ток, заряд и т. д.), определенным образом связанную с передаваемым сообщением. Во втором случае то же сообщение содержится в последовательности двоично-кодированных чисел.

Сигналы, формируемые в радиопередающих устройствах и излучаемые в пространство, а также поступающие в приемное устройство, где они подвергаются усилению и некоторым преобразованиям, являются физическими процессами.

В предыдущем параграфе указывалось, что для передачи сообщений на расстояние используются модулированные колебания. В связи с этим сигналы в канале радиосвязи часто подразделяют на управляющие сигналы и на радиосигналы; под первыми понимают модулирующие, а под вторыми — модулированные колебания.

Обработка сигналов в виде физических процессов осуществляется с помощью аналоговых электронных цепей (усилителей, фильтров и т. д.). Обработка сигналов, закодированных в цифру, осуществляется с помощью вычислительной техники.

Представленная на рис. 1.1 структурная схема канала связи не содержит указаний о виде используемого для передачи сообщения сигнала и структуре отдельных устройств. Между тем сигналы от источника сообщений, а также после детектора (рис. 1.1) могут быть как непрерывные, так и дискретные (цифровые). В связи с этим применяемые в современной радиоэлектронике сигналы можно разделить на следующие классы:

- произвольные по величине и непрерывные по времени (рис. 1.2, а);

- произвольные по величине и дискретные по времени (рис. 1.2, б).

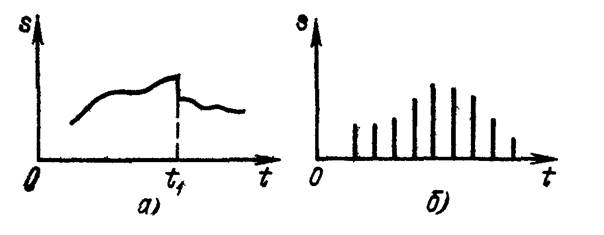
Рис. 1.2. Сигналы произвольные по величине и непрерывные

по времени (а), произвольные по величине и дискретные по времени (б)

Сигналы первого класса (рис. 1.2, а) иногда называют аналоговыми, так как их можно толковать как электрические модели физических величин, или непрерывными, так как они задаются по оси времени на несчетном множестве точек. Такие множества называются континуальными. При этом по оси ординат сигналы могут принимать любое значение в определенном интервале. Поскольку эти сигналы могут иметь разрывы, как на рис. 1.2, а, то, чтобы избежать некорректности при описании, лучше такие сигналы обозначать термином континуальный.

Итак, континуальный сигнал S(t) является функцией непрерывной переменной t, а дискретный сигнал S(x) — функцией дискретной переменной х, принимающей только фиксированные значения. Дискретные сигналы могут создаваться непосредственно источником информации (например, дискретными датчиками в системах управления или телеметрии) или образовываться в результате дискретизации континуальных сигналов.

На рис. 1.2, б представлен сигнал, заданный при дискретных значениях времени t (на счетном множестве точек); величина же сигнала в этих точках может принимать любое значение в определенном интервале по оси ординат (как и на рис. 1.2, а). Таким образом, термин дискретный характеризует не сам сигнал, а способ задания его на временной оси.

Особой разновидностью дискретных сигналов являются цифровые сигналы. Они характерны тем, что отсчетные значения сигнала представлены в форме чисел.

Таким образом, можно различать континуальные (рис. 1.2, а), дискретные (рис. 1.2, б), и цифровые сигналы.

1.2. Представление произвольного сигнала посредством суммы

элементарных сигналов

Любой реальный сигнал приближенно представляется суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени. Выбор элементарных сигналов произволен. Однако широкое применение нашли два способа представления. Согласно первому из них в качестве элементарных сигналов используются ступенчатые функции, возникающие через равные промежутки времени Δ (рис. 1.3, а). Высота каждой ступеньки равна приращению сигнала на интервале времени Δ.

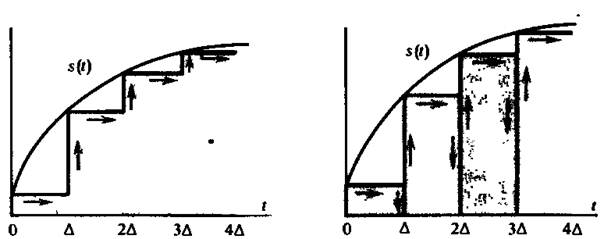
а б

Рис. 1.3. Способы представления сигналов

При втором способе элементарными сигналами служат прямоугольные импульсы. Эти импульсы непосредственно примыкают друг к другу и образуют последовательность, вписанную в кривую или описанную вокруг нее (рис. 1.3,6).

Для представления сигнала по первому способу используют в качестве математической модели элементарного сигнала так называемую функцию включения или функцию Хевисайда:

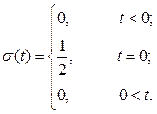
Это есть предел, к которому стремится некоторая функция

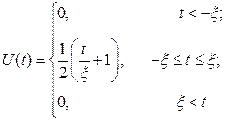
при ξ→ 0. В общем случае функция включения, может быть смещена относительно начала отсчета времени на величину t ₀. Запись смещенной функции такова:

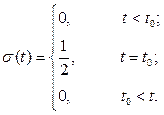(1.1)

При представлении сигнала S (t), с помощью функции включения положим, что S (t) = 0 при t < 0. Пусть {Δ, 2Δ, 3Δ,...} — последовательность моментов времени и { S ₁, S ₂, S ₃, …} — отвечающая им последовательность значений сигнала. Если S ₀ = S (0) — начальное значение сигнала, то текущее значение сигнала при любом t приближенно равно сумме ступенчатых функций:

.

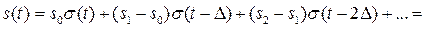
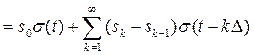Это равенство тем точнее, чем меньше шаг Δ. В пределе при Δ→ 0 равенство становится точным.

Прежде чем перейти ко второму способу динамического представления сигнала, когда элементами разложения служат короткие импульсы, следует ввести новое важное понятие.

Рассмотрим импульсный сигнал прямоугольной формы, заданный следующим образом:

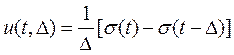. (1.2)

Этот импульс характерен тем, что при любом выборе параметра Δ площадь этого импульса равна единице:

.

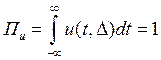Пусть теперь величина Δ стремится к нулю. Импульс, сокращаясь по длительности, сохраняет свою площадь, поэтому его высота должна неограниченно возрастать. Предел последовательности таких функций при Δ→ 0 носит название дельта-функции, или функции Дирака:

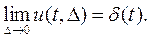
Дельта-функция — интересный математический объект. Будучи равной нулю всюду, за исключением точки t = 0 ((принято говорить, что она сосредоточена в этой точке), эта функция тем не менее обладает единичным интегралом

.

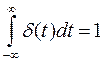Вернемся теперь к задаче описания аналогового сигнала суммой примыкающих друг к другу прямоугольных импульсов (см. рис. 1.3,6). Если S_k — значение сигнала на k -том отсчете, то элементарный импульс с номером k представляется так:

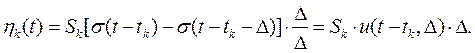
Исходный сигнал S (t) должен рассматриваться как сумма таких элементарных слагаемых:

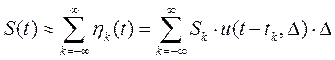. (1.3)

В пределе при Δ→ 0

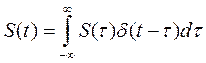. (1.4)

Итак, если непрерывную функцию умножить на дельта-функцию и произведение проинтегрировать по времени, то результат будет равен значению непрерывной функции в той точке, где сосредоточен дельта-нмпульс. Принято говорить, что в этом состоит фильтрующее свойство дельта-функции.

1.3. Энергетические характеристики вещественного сигнала

Основными энергетическими характеристиками вещественного сигнала S (t)являются:

1) мгновенная мощность p (t), определяемая как квадрат мгно­венного значения сигнала

p (t) = S² (t).

Если S (t)— напряжение или ток, то p (t)— мгновенная мощность, выделяемая на сопротивлении в 1 Ом.

Мгновенная мощность не аддитивна, т. е. мгновенная мощ­ность суммы сигналов не равна сумме их мгновенных мощностей, т.е. если S (t) = S ₁(t) + S ₂(t), то

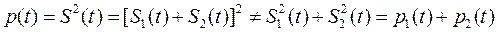
2) энергия Эна интервале времени (t ₁, t ₂)выражается как интеграл от мгновенной мощности

.

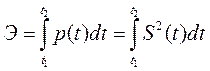3) средняя мощность P _ср на интервале (t ₁, t ₂) определяется
значением энергии сигнала на этом интервале, отнесенной к еди­нице времени

,

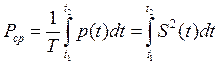где T = t ₁ — t ₂. Далее вместо средней мощности P _ср будем для краткости писать просто мощность Р.

Энергия и мощность сигналов, определяемые на произвольном интервале времени, могут быть аддитивными, если сигналы на этом интервале времени ортогональны. Рассмотрим два сигнала S ₁(t) и S ₂(t), которые заданы на интервале времени T = t ₁ — t ₂. Энергия и мощность суммы этих сигналов выражаются следующим образом:

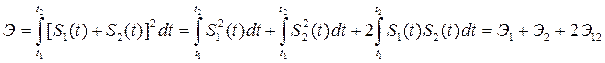
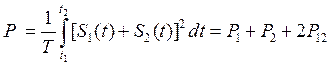
Здесь Э₁, P ₁ и Э₂, P ₂ — энергия и мощность первого и второго сигналов, Э₁₂ и P ₁₂— взаимная энергия и взаимная мощность этих сигналов (или энергия и мощность их взаимодействия). Если выполняется условие

,

то сигналы S ₁(t) и S ₂(t) на интервале времени T = t ₁ — t ₂ называют ор­тогональными и выражения и тогда

Э = Э ₁ + Э ₂; P = P ₁ + P ₂.

Образно говоря, сигналы S ₁(t) и S ₂(t) ортогональны, если они предельно непохожи друг на друга.

1.4. Геометрические методы в теории сигналов

Любой вектор N -мерного линейноговекторного пространства полностью характеризуется своими проекциями на N координат­ных осей. Например,длина и направление двумерного вектора А о пределяется двумя его проекциями а_х и а_у на координатные оси х и у (рис. 1.4).

Для разложения векторов удобно использовать взаимно пер­пендикулярные оси, удовлетворяющие условию ортонормированности:

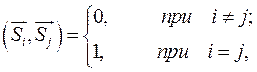
где 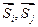— единичные координатные векторы (орты), a i и j — индексы, присвоенные координатным осям 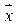(орт , орт ).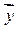

Условие ортонормированности означает, что скалярное произведе­ние 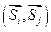любых двух векторов 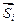и 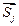должно быть равно ну­лю, а скалярное произведение любого вектора самого на себя должно быть равно единице. Напомню, что если имеется два вектора 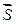и 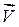то их скалярное произведение определяется следующим образом:

,

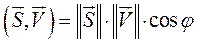где φ – угол между векторам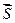и и .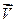

Если вектор задан в N – мерном пространстве, то его можно разложить на N векторов, т. е. выразить суммой вида

.

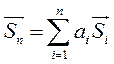Здесь a_i — проекция вектора 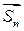на i – ю координатную ось, направление которой задается соответствующим координатным вектором 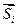. Число линейно-независимых векторов, составляющих базис 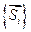, равно размерности векторного пространства. Полной координат­ной системой для заданного ансамбля векторов считается такая, которая позволяет осуществить точное разложение любого векто­ра из заданного ансамбля.

По аналогии с вектором сигнал (ко­нечной мощности или энергии) можно представить точкой N – мерного функционального (сигнального) пространства. Эта точка яв­ляется концом вектора, идущего из начала координат. Поэтому любой сигнал может быть охарактеризован своими «проекциями» на координатные оси, «направление» которых задается рядом функций.

Для разложения сигналов наиболее удобными оказываются некоторое множество функций (координатный базис), удовлетворяющий условию ортонормированности

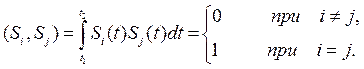
Здесь [ t ₁, t ₂] – интервал времени, на котором определены сигналы S_i (t).

Пространство (векторное или функциональное) называют мет­рическим, если введен способ определения расстояния между его двумя точками, и нормированным, если введено понятие нормы, т. е. расстояния между началом координат и какой-либо точкой пространства. Метрику линейного векторного пространства можно определитьчерез скалярное произведение векторов.

Так, длина вектора 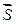, определяющая расстояние от начала координат до некоторой точки пространства, т. е. норма ||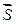|| ли­нейного векторного пространства может быть определена скаляр­ным произведением 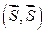вектора на самого себя

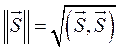
или через проекции а_х, а_у, a_z... вектора 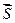на координатные оси x, у, z.

Аналогично расстояние от начала координат до точки, отобра­жающей функцию s(t), т.е. норма сигнального пространства ||S|| выражаетсясредней мощностью сигнала (скалярным произведе­нием сигнала на самого себя)

.

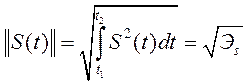Расстояние между двумя векторам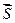и и 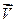, метрика векторного пространства, определяется как модуль разностноговектора 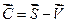, т.е.

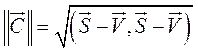
или через проекции а_х, b_х, а_у, b_у,... векторов 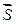и 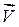на координатные оси х, у

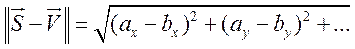
Аналогичноможет быть определено и расстояние между дву­мя сигналами S (t)и U (t), т. е. метрика сигнального пространства

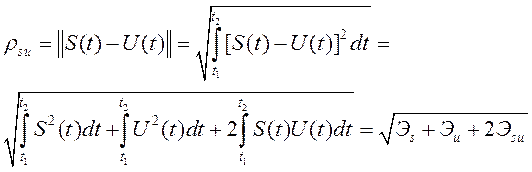
Линейное векторное пространство (конечномерное), в котором введено понятие скалярного произведения, является Евклидовым. При бесконечной размерности то же пространство называется Гильбертовым .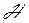

Векторное отображение сигналов нашло широкое применение в радиотехнике, так как оно позволяет наглядно представлять взаимодействие сигналов, степени их различия и подобия, вероят­ность перехода одного сигнала в другой под действием помех и т. д.

1.5. Разложение сигнала в обобщенный ряд Фурье

Пусть 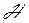— гильбертово пространство сигналов с конечным значением энергии. Эти сигналы определены на отрезке времени [ t ₁, t ₂], конечном или бесконечном. Предположим, что на этом же отрезке задана бесконечная система функций { u ₁, u ₂, u ₃, …. u_n, …}, попарно ортогональных друг другу и обладающих единичными нормами:

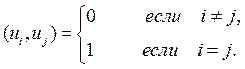(1.6)

Говорят, что при этом в пространстве сигналов задан ортонормированный базис.

В этом случае произвольный сигнал 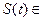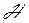можно представить суммой:

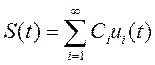(1.7)

Данное выражение называется обобщенным рядом Фурье сигнала S (t) в выбранном базисе.

Коэффициенты этого ряда находят следующим образом. Возьмем базисную функцию u_k с произвольным номером k, умножим на нее обе части равенства 1.7) b затем проинтегрируем результаты по интервалу времени, на котором заданы сигналы

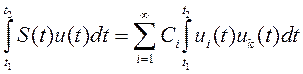. (1.8) Ввиду ортонормированности базиса в правой части равенства (1.8) останется только одно слагаемое с номером i = k, поэтому

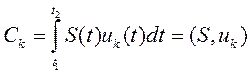. (1.9)

Возможность представления сигналов посредством обобщенного ряда Фурье является фактом большого принципиального значения. Вместо того чтобы изучать функциональную зависимость в несчетном множестве точек, мы получаем возможность характеризовать эти сигналы счетной (но, вообще говоря, бесконечной) системой коэффициентов обобщенного ряда Фурье С_k. Эти коэффициенты представляют собой “проекции” вектора S (t) в гильбертовом пространстве на базисные направления.

Вычислим энергию сигнала, представленного рядом (1.7)

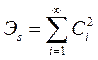. (1.10)

Поскольку базисная система функций ортонормирована, в сумме (1.10) отличными от нуля окажутся только слагаемые с номерами i = j. Отсюда получается замечательный результат:

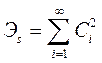. (1.11)

Это обобщение теоремы Пифагора для случая бесконечномерного пространства. Смысл этой формулы таков: энергия.сигнала есть сумма энергий всех компонент, из которых складывается обобщенный ряд Фурье.

Если мы учитываем не все слагаемые обобщенного ряда Фурье, то

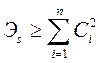(неравенство Бесселя).

Оно означает, что энергия приближенной копии сигнала S (t), полученной в результате его аппроксимации рядом

,

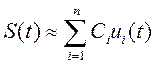Меньше или равна энергии оригинала. При этом ошибка аппроксимации

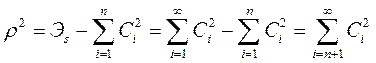
При увеличении n уменьшается.

Выбор наиболее рациональной ортогональной системы функций зависит от цели, преследуемой при разложении сложной функции в ряд. Среди разнообразных задач, требующих разложения сложного сигнала, наиболее важными являются:

1) точное разложение на простейшие ортогональные функции;

2) аппроксимация сигналов, процессов или характеристик, когда требуется свести к минимуму число членов ряда (при заданной допустимой погрешности).

При первой постановке задачи наибольшее распространение получила ортогональная система основных тригонометрических функций — синусов и косинусов. Это объясняется рядом причин. Во-перзых, гармоническое колебание является простейшей функцией, определенной при всех значениях t. Во-вторых, гармоническое колебание является единственной функцией времени, Сохраняющей свою форму при прохождении колебания через линейную систему.

В последнее время под влиянием методов обработки дискретных сигналов широкое распространение получила ортонормированная система функций Уолша. Эти функции характерны тем, что на интервале своего существования [- T /2, T /2] они принимают лишь значения ±1. Введем безразмерное время θ = t/T и будем обозначать k -ю функцию Уолша, как это принято, символом wal { k, θ). Идею образования функций Уолша легко усмотреть из, рис. 1.4, на котором изображены графики нескольких первых функций Уолшв. Интересно отметить, что номер функции k равен числу перемен знака на интервале ее существования.

При второй постановке задачи, приближенном разложении функции, применяются разнообразные системы ортогональных функций: полиномы Чебышева, Эрмита, Лагерра, Лежандра и многие другие. С некоторыми из них можно ознакомиться в учебнике Гоноровского.

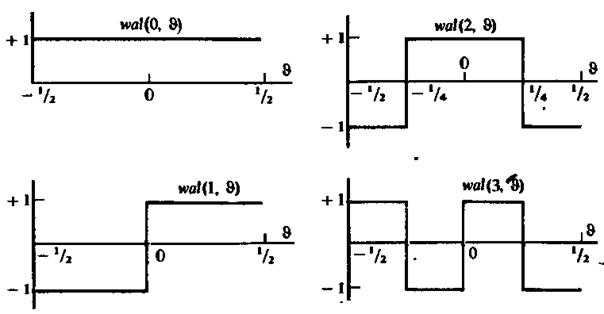
Рис. 1.4. Графики нескольких первых функций Уолша

1.6. Гармонический анализ периодических сигналов

Ранее было отмечено, что для периодического сигнала справедливо равенство

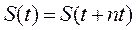, n =±1, ±2, ±3, … T – период сигнала.

При гармоническом анализе в качестве ортонормированного базиса берут функции:

....

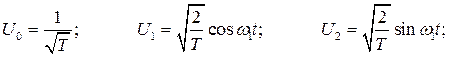
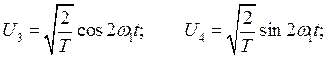Интервал ортогональности совпадает с периодом Т = 2π/ω₁ функции S (t). Выполнив разложение сигнала S (t) в этом базисе, т. е. вычислив коэффициенты C_m = (S,U_m), получим его спектральное представление

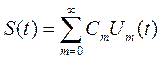(1.11)

Разложение справедливо на всей бесконечности оси времени. Ряд вида (1.11) называется рядом Фурье данного сигнала.

Вычисляя коэффициенты разложения, ряд (1.11) можно записать в виде

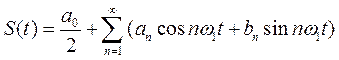, (1.12)

Где коэффициенты

,

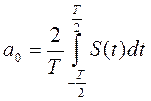, (1.13)

.

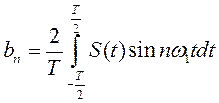Итак, в общем случае периодический сигнал содержит независящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами ω_n = nω ₁ , (n = 1, 2, 3,...), кратными основной частоте последовательности.

Каждую гармонику можно описать ее амплитудой А_n и начальной фазой φ_n. Для этого коэффициенты ряда Фурье следует записать в виде

так что

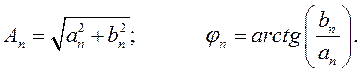
Подставив эти выражения в (1.12), получим другую, эквивалентную форму ряда Фурье:

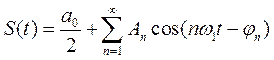, (1.14)

которая иногда оказывается удобнее.

Спектральная диаграмма периодического сигнала. Так принято называть графическое изображение коэффициентов ряда Фурье для конкретного сигнала. Различают амплитудные и фазовые спектральные диаграммы (рис. 1.5). Здесь по горизонтальной оси в некотором масштабе отложены частоты гармоник, а по вертикальной оси представлены их амплитуды и начальные фазы.

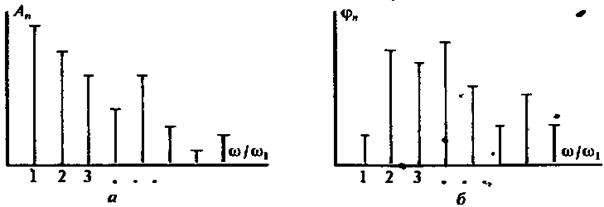
Рис. 1.5. Спектральные диаграммы некоторого периодического сигнала:

а — амплитудная; б — фазовая

Особо интересуются амплитудной диаграммой, которая позволяет судить о процентном содержании тех или иных гармоник в спектре периодического сигнала.

2.4. Спектры простейших периодических сигналов

Рассмотрим несколько примеров периодических колебаний, часто используемых в различных радиотехнических устройствах.

1. ПОСЛЕДОВАТЕЛЬНОСТЬ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ

Подобное колебание (рис. 1.6) находит широкое применение в измерительной технике. Применяя формулу (1.13), находим среднее значение (постоянную составляющую)

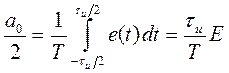
и коэффициент n – й гармоники

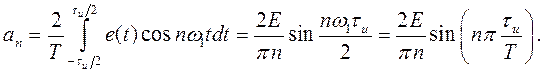
Так как функция е (t) четная, b_n = 0 и A_n = | a_n |. Таким образом,

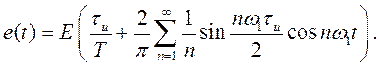(1.15)

Величина q = T / τ _и называется скважностью импульсной последовательности. При больших значениях q спектр сигнала содержит большое число медленно убывающих по амплитуде гармоник (рис. 1.7). Расстояние между спектральными линиями мало, а амплитуды соседних гармоник близки по величине.

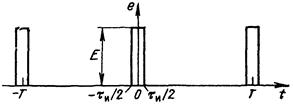
Рис. 1.6. Периодическая последовательность прямоугольных импульсов

с большой скважностью

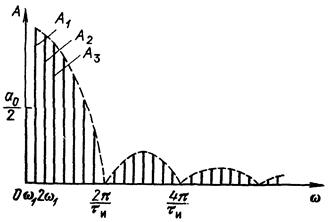
Рис. 1.7. Спектр импульсной

последовательности

При значении скважности q = 2, выражение (1.15) принимает следующий вид:

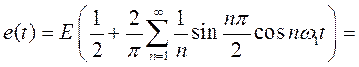
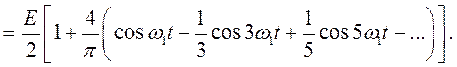
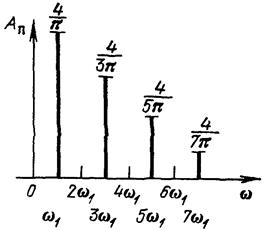Спектральная диаграмма колебания, соответствующая данному случаю, представлена на рис 1.8.

Рис. 1.8. Спектр импульсной

последовательности при q = 2

2. ПОСЛЕДОВАТЕЛЬНОСТЬ ПИЛООБРАЗНЫХ ИМПУЛЬСОВ

С подобными функциями (рис. 1.8) часто приходится иметь дело в устройствах для развертки изображения в осциллографах. Так как эта функция является нечетной, ряд Фурье для нее содержит только синусоидальные члены. С помощью формул (1.13) нетрудно определить коэффициенты ряда Фурье. Опуская эти выкладки, напишем окончательное выражение для ряда

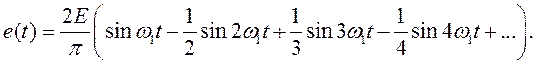
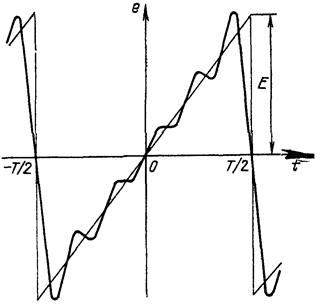Как видим, амплитуды гармоник убывают по закону 1/ n, где n = 1, 2, 3,... На рис. 1.9 показан график суммы первых пяти гармоник (в увеличенном масштабе).

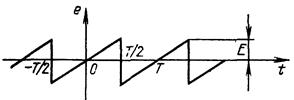
Рис. 1.8. Периодическое колебание

пилообразной формы

Рис. 1.9. Сумма первых пяти гармоник

колебания, показанного на рис. 1.8

3. ПОСЛЕДОВАТЕЛЬНОСТЬ УНИПОЛЯРНЫХ ТРЕУГОЛЬНЫХ ИМПУЛЬСОВ

Ряд Фурье для этой функции (рис. 1.10) имеет следующий вид:

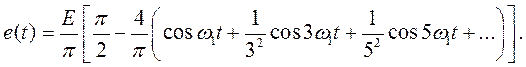
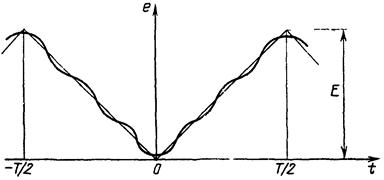На рис. 1.10 изображена сумма первых четырех слагаемых этого ряда. В данном случае отметим более быстрое убывание амплитуд гармоник, чем в предыдущих примерах. Это объясняется отсутствием разрывов (скачков) в функции.

Рис. 1.10. Сумма четырех

слагаемых ряда Фурье для

периодической функции

1.8. Гармонический анализ непериодических сигналов.

1.8.1. Комплексная форма ряда Фурье.

Прежде чем перейти к гармоническому анализу непериодических сигналов перепишем ряд (13), применив формулу Эйлера, в соответствии с которой

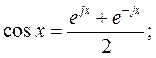
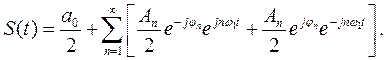(1.16)

Введем новые коэффициенты

Тогда ряд (1.16) можно представить следующим образом

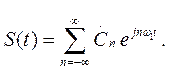(1.17)

Формула (1.17) является рядом Фурье в комплексной форме, коэффициенты такого ряда

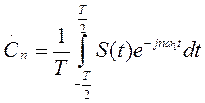. (1.18)

1.8.2. Спектральная плотность сигнала

Теперь распространим изложенный в подразделе 1.6 гармонический анализ периодических сигналов на некоторый непериодический сигнал.

Пусть такой сигнал S (t) задан в виде некоторой функции, отличной от нуля в промежутке [ t ₁, t ₂] (рис. 1.6). Выделив произвольный отрезок времени T, включающий в себе промежуток [ t ₁, t ₂], мы можем представить заданный сигнал в виде ряда Фурье:

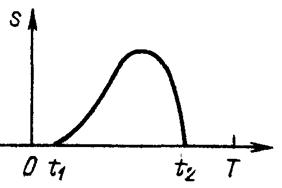
Рис. 1.6. Одиночный импульс

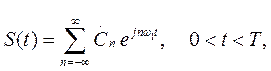(1.19)

где 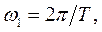а коэффициенты 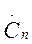в соответствии с формулой (1.18)

.

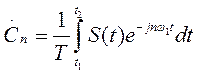Введем обозначение

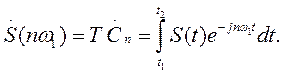(1.20)

Подстановка (1.20) в (1.19) приводит к следующему результату

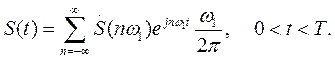(1.21)

Здесь учтено, что Т =2π/ω₁.

Вне отрезка (О, T) ряд (1.19) определяет функцию S (t) = S (t ± kT), где k — целое число, т. е. периодическую функцию, полученную повторением S (t) вправо и влево с периодом Т. Для того чтобы вне отрезка (О, Т) функция равнялась нулю, величина Т должна быть бесконечно большой. Но чем больше отрезок Т, выбранный в качестве периода, тем меньше коэффициенты C_n. Устремляя Т к бесконечности, в пределе получаем бесконечно малые амплитуды гармонических составляющих, сумма которых изображает исходную непериодическую функцию S (t), заданную в интервале t ₁ < t < t ₂ (см. рис. 1.6). Число гармонических составляющих, входящих в ряд Фурье, будет при этом бесконечно большим, так как при Т → ∞ основная частота функции ω₁ = (2л/ Т) → 0. Иными словами, расстояние между спектральными линиями, равное основной частоте ω₁ становится бесконечно малым, а спектр — сплошным. Поэтому в выражении (1.21) можно заменить ω₁ на d ω, n ω₁ на текущую частоту ω, а операцию суммирования операцией интегрирования. Таким образом, приходим к интегралу Фурье

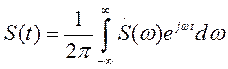, (1.22)

в котором в соответствии с (1.20)

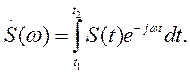
В общем случае, когда пределы t ₁ и t ₂ не уточнены

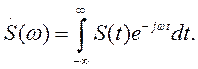(1.23)

Функция S (ω) называется спектральной плотностью или спектральной характеристикой сигнала S (t). Выражение (1.23) называется прямым преобразованием Фурье данного сигнала. Формула (1.22) называется обратным преобразованием Фурье.

1.8.3. Физический смысл спектральной плотности

Если применить формулу Эйлера, в соответствии с которой

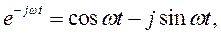
то выражение (1.23) можно переписать в следующем виде:

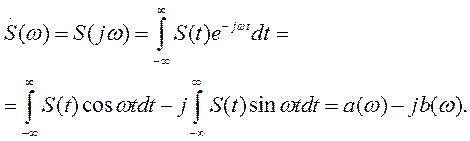
Модуль и аргумент спектральной плотности определяются выражения-

ми

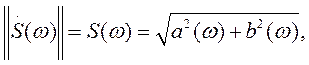
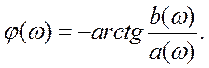
Первое из этих выражений можно рассматривать как амплитудно-частотную (АЧХ), а второе — как фазо-частотную характеристики (ФЧХ) сплошного спектра непериодического сигнала S (t). Как и в случае ряда Фурье, S (ω) является четной, а φ(ω) — нечетной функцией частоты ω.

С учетом вновь введенных обозначений, выражение для спектральной плотности можно записать в показательной форме

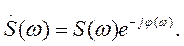(1.24)

На основании формулы (1.24) нетрудно привести интегральное преобразование (1.22) к тригонометрической форме (аргумент функции φ (ω) в последующих выражениях опущен):

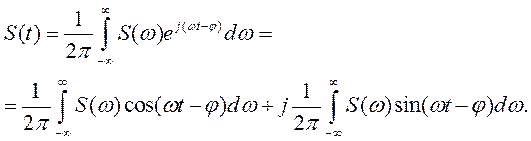
Из четности модуля и нечетности фазы следует, что подынтегральная функция в первом интеграле является четной, а во втором — нечетной относительно ω. Следовательно, второй интеграл равен нулю и окончательно

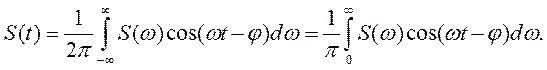
Сравним последнее выражение с формулой (1.14)

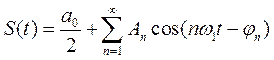(1.14)

Из сопоставления выражений видно, что величина

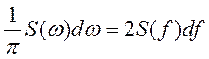
имеет смысл амплитуды A_n (бесконечно малой) гармонической составляющей частоты ω = 2 πf. Из сопоставления становится ясным физический смысл термина спектральная плотность. 2 S (f) — это амплитуда сигнала, приходящаяся на один герц в бесконечно узкой полосе частот, включающей в себя частоту f.

Отметим, что при ω = 0 выражение (1.23) переходит в следующее:

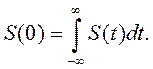(1.25)

Следовательно, для любого сигнала S (t) значение спектральной плотность S (ω) на нулевой частоте равно «площади сигнала». Это правило полезно для быстрого выявления структуры спектра некоторых сигналов.

1.8.4. Соотношение между спектрами одиночного импульса и

периодической последовательности импульсов

Пусть заданы импульс S ₁(t) и соответствующая ему спектральная плотность S ₁(ω) = S ₁(2π f) (рис. 1.7, а). На этом рисунке изображен модуль сплошного спектра S ₁(2π f) в виде функции, четной относительно f.

При повторении импульсов с периодом Т получается последовательность, представленная на рис. 1.7, б (слева). Линейчатый (дискретный) спектр этой последовательности изображен в правой части рисунка. При периоде Т интервал между любыми двумя соседними гармониками равен f ₁ = 1/ T.

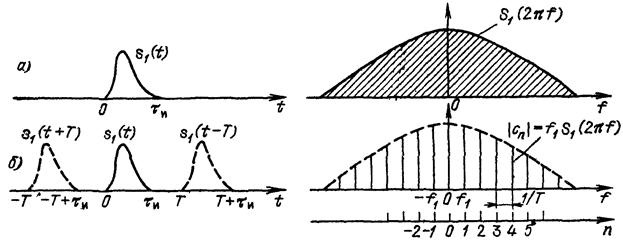
Рис. 1.7. Одиночный импульс и его спектральная плотность (а), периодическая последовательность импульсов и ее линейчатый спектр (б)

Сравним формулы (1.23) для S (ω) и (1.18) для коэффициента 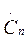ряда Фурье

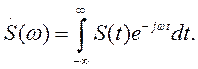(1.23)

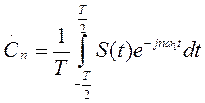. (1.18)

Из сравнения следует, что спектральная плотность S (ω=nω ₁) отличается от коэффициента C_n ряда Фурье периодической последовательности только отсутствием множителя 1/ T. Следовательно, при повторении импульса S (t) с периодом Т, коэффициенты ряда Фурье для полученной периодической последовательности, связаны со значением спектральной плотности одиночного импульса на частоте ω=nω ₁, простым соотношением

.

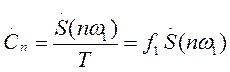Для уяснения связи между амплитудой k -ой, гармоники A_k, периодической последовательности импульсов и модулем спектральной плотности одиночного импульса рассмотрим два слагаемых ряда Фурье

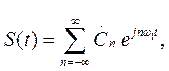
Соответствующих значениям n = k и n = - k

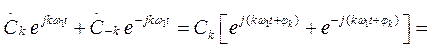
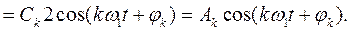
Следовательно

.

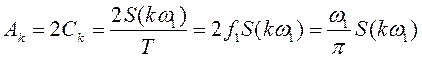Итак, модуль спектральной плотности одиночного импульса и огибающая линейчатого спектра периодической последовательности, полученной путем повторения заданного импульса, совпадают по форме и отличаются только масштабом.

На рис. 1.7, б штриховой линией обозначена огибающая линейчатого

спектра | C_n | = f ₁ S ₁(nω ₁).

1.9. Примеры определения спектров сигналов

1. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ПРЯМОУГОЛЬНОГО ИМПУЛЬСА

Простейшее колебание, определяемое выражением

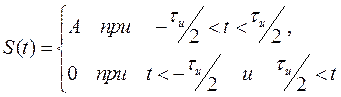
и представленное на рис. 1.8, а, получило широкое распространение как в технике, так и в теории сигналов и цепей. Применяя формулу (1.23), находим спектральную плотность (рис. 1.8, б)

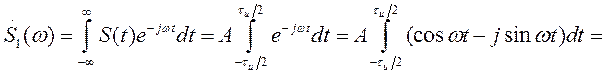
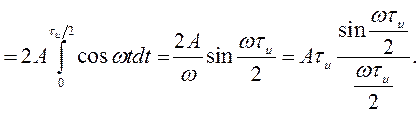
Заметим, что произведение Aτ _и, равное площади импульса, определяет

значение спектральной плотности импульса при ω = 0, т. е. S ₁(0) = Aτ _и [см. (1.25)].

При удлинении (растягивании) импульса расстояние между нулями функции S ₁(ω) сокращается, что равносильно сужению спектра. Значение S ₁(0) при этом возрастает. При укорочении (сжатии) импульса, наоборот, расстояние между нулями функции S ₁(ω) увеличивается (расширение спек- тра), а значение S ₁(0) уменьшается. В пределе при τ _и → 0 (А = const) точки ω ₁ = ±2π/ τ _и, соответствующие двум первым нулям функции S ₁(ω), удаляются в бесконечность и спектральная плотность, бесконечно малая по величине, становится равномерной в полосе частот от ─ ∞ до ∞.

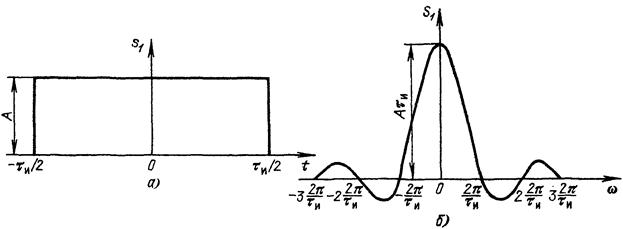
Рис. 1.8. Прямоугольный импульс (а) и его спектральная плотность (б)

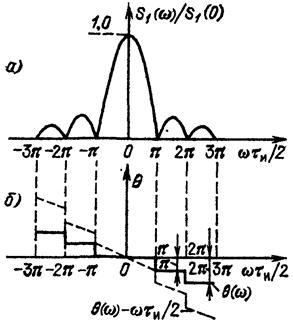На рис. 1.9 показаны отдельно графики модуля S ₁(ω), отнесенного к величине S ₁(0), и аргумента θ (ω) спектральной плотности. Первый из этих графиков можно рассматривать как АЧХ, а второй — как ФЧХ спектра прямоугольного импульса. Каждая перемена знака S ₁(ω) учитывается на рис. 1.9, б приращением фазы на π.

Рис. 1.9. Модуль (а) и аргумент (б) спек-

тральной плотности прямоугольного →

импульса

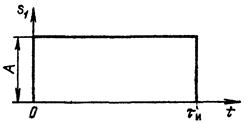
Рис. 1.10. Совмещение начала отсчета вре-

мени с фронтом прямоугольного импульса

При отсчете времени не от середины импульса (как на рис. 1. 8), а от фронта (рис. 1.10) ФЧХ спектра импульса должна быть дополнена слагаемым ωτ _и /2, учитывающим сдвиг импульса на время τ _и /2 (в сторону запаздывания). Результирующая ФЧХ принимает при этом вид, показанный на рис. 1.9, б штриховой линией.

2. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ДЕЛЬТА – ФУНКЦИИ

Пусть сигнал S (t) представляет собой короткий импульс, сосредоточенный в точке t = 0 и имеющий площадь А. Такой сигнал имеет математическую модель S (t) = Aδ (t). Спектральная плотность этого сигнала

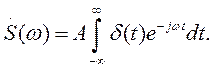
На основании фильтрующего свойства дельта-функции (см. разд. 1.3) входящий сюда интеграл численно равен значению непрерывной функции в той точке, где сосредоточен дельта-импульс. Поэтому

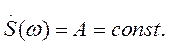
Итак, дельта-импульс имеет равномерный спектр на всех частотах.

Связь между длительностью импульса и шириной его спектра. Если проанализировать частные случаи, изученные выше, то можно сделать очень важный вывод: чем меньше длительность импульса, тем шире его спектр.

Под шириной спектра здесь и в дальнейшем будем понимать частотный интервал, в пределах которого модуль спектральной плотности не меньше некоторого наперед заданного уровня, например изменяется в пределах от | S |_max до 0,1| S |_max.

Рассмотрим прямоугольный видеоимпульс, полагая при этом, что верхняя граничная частота спектра ω _в — это частота, соответствующая первому нулю спектральной плотности. Нетрудно видеть, что

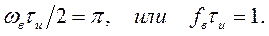
Итак, произведение ширины спектра импульса на его длительность есть постоянное число, зависящее только от формы импульса и, как правило, имеющее порядок единицы. Говорят, что ширина спектра и длительность импульса связаны соотношением неопределенности (термин, заимствованный из квантовой механики).

Это соотношение имеет первостепенное значение для радиотехники. Оно определяет требования к ширине полосы пропускания радиотехнического устройства. Например, чем короче длительность импульса, тем шире должна быть полоса пропускания соответствующего усилителя. Короткие импульсные помехи имеют широкий спектр и поэтому могут ухудшать условия радиоприема в значительной полосе частот.

1.10 Некоторые свойства преобразования Фурье

Между сигналом S (t) и его спектром S (ω) существует однозначное соответствие. Для практических приложений важно установить связь между преобразованием сигнала и соответствующим этому преобразованию изменением спектра. Из многочисленных возможных преобразований сигнала рассмотрим следующие наиболее важные и часто встречающиеся: сдвиг сигнала во времени, изменение масштаба времени, сдвиг спектра сигнала по частоте, дифференцирование и интегрирование сигнала. Кроме того, будут рассмотрены сложение сигналов, произведение и свертка двух сигналов.

1. СДВИГ СИГНАЛОВ ВО ВРЕМЕНИ

Пусть сигнал S ₁(t) произвольной формы существует на интервале времени от t ₁ до t ₂ и обладает спектральной плотностью S ₁(ω). При задержке этого сигнала на время t ₀ (при сохранении его формы) получим новую функцию времени

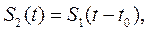
существующую на интервале от t ₁ + t ₀ до t ₂ + t ₀.

Спектральная плотность сигнала S ₂(t) в соответствии с (1.23)

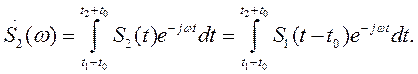
Вводя новую переменную интегрирования τ = t — t ₀, получаем

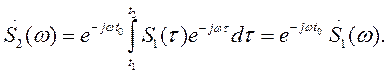
Из этого соотношения видно, что сдвиг во времени функции S (t) на ± t ₀ приводит к изменению фазовой характеристики спектра S (ω) на величину ± ωt ₀. Очевидно и обратное положение: если всем составляющим спектра функции S (t) дать фазовый сдвиг φ (ω) = ± ωt ₀, линейно-связанный с частотой ω, то функция сдвигается во времени на ± t ₀.

Амплитудно-частотная характеристика спектра (т. е, модуль спектральной плотности) от положения сигнала на оси времени не зависит.

2. ИЗМЕНЕНИЕ МАСШТАБА ВРЕМЕНИ

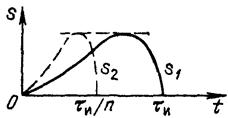Пусть сигнал S ₁(t), изображенный на рис. 1.11 сплошной линией, подвергся сжатию во времени. Новый сжатый сигнал S ₂(t) (штриховая кривая на рис. 1.11) связан с исходным соотношением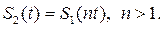

Длительность импульса S ₂(t) в n раз меньше, чем исходного, и равна τ _и./ n. Спектральная плотность сжатого импульса

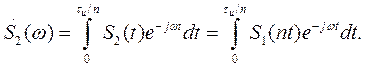Рис. 1.11. Сжатие сигнала

Вводя новую переменную интегрирования τ = nt, получаем

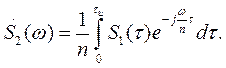
Но интеграл в правой части этого выражения есть не что иное, как спектральная плотность исходного сигнала S ₁(t) при частоте ω / n, т. е. S ₁(ω / n).

Таким образом,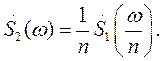

Итак, при сжатии сигнала в n раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшается в n раз. Очевидно, что при растягивании сигнала во времени (т. е. при n <. 1) имеют место сужение спектра и увеличение модуля спектральной плотности.

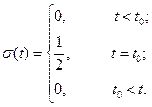
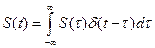
Под структурой управления организацией понимается упорядоченная совокупность взаимосвязанных элементов, находящихся между собой в устойчивых отношениях, обеспечивающих их функционирование и развитие как единого целого.

К элементам структуры относят отдельных работников организации, службы, отделы и другие звенья аппарата управления. В любой ОСУ каждый ее элемент имеет определенное место и соответствующие связи, посредством которых в процессе управления возникает взаимодействие элементов (прямые и косвенные связи).

Отношения между ними определяются и поддерживаются благодаря организационным связям четырех типов:

• горизонтальные;
• вертикальные;
• линейные;
• функциональные;
• межфункциональные.

Горизонтальные связи – связи, закрепляющие характер согласования элементов; как правило, одноуровневые.

Вертикальные связи – связи, закрепляющие характер подчинения элементов при иерархичности управления в организации; как правило, многоуровневые (т.е. характеризуют наличие нескольких уровней управления).

Линейные связи – связи между линейными руководителями, характеризующие движение управленческих решений и информации между ними. Возникают между подразделениями и руководителями разных уровней управления. Обычно данный вид связей появляется там, где один руководитель административно подчиняется другому.

Функциональные связи – связи между основными функциями управления в организации, характеризующие движение информации и управленческих реше

Дата добавления: 2013-12-12