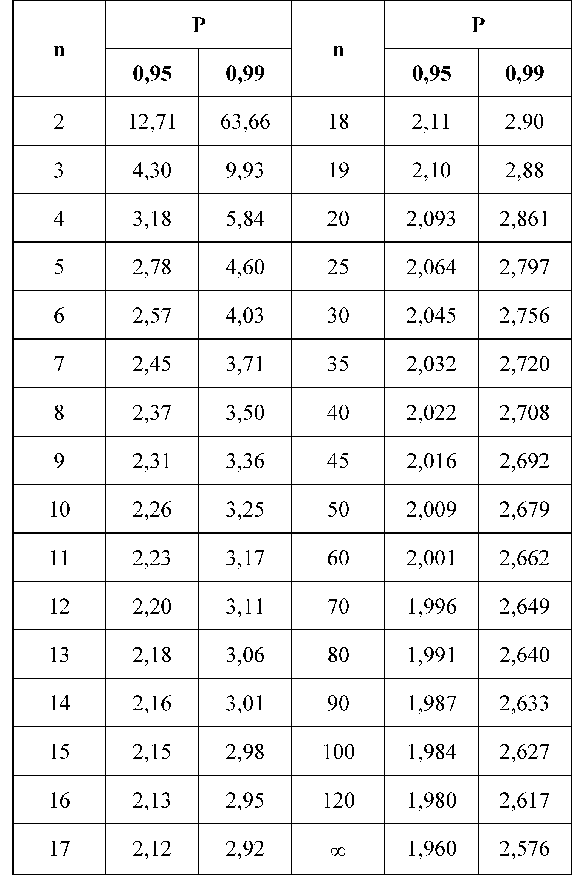
Значения t-критерия Стьюдента для вероятности 0,95 и 0,99

Пример 3. Из работников фирмы случайным образом отобрано 30 человек. По выборке оказалось, что средняя зарплата (в месяц) составляет 10 тыс. рублей при среднем квадратическом отклонении 3 тыс. рублей. С вероятностью 0,99 определить среднюю зарплату в фирме.

Решение: По условию имеем n = 30, Х_ср.=10000, S=3000, Р = 0,99. Для нахождения доверительного интервала воспользуемся формулой, соответствующей критерию Стьюдента. По таблице для n = 30 и Р = 0,99 находим t=2,756, следовательно,

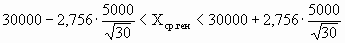
т.е. искомый доверительный интервал 27484 < Х_ср.ген < 32516. Итак, вероятностью 0,99 можно утверждать, что интервал (27484; 32516) содержит внутри себя среднюю зарплату в фирме. Мы надеемся, что Вы будете пользоваться этим методом, при этом не обязательно, чтобы при Вас каждый раз была таблица. Подсчеты можно проводить в Excel автоматически. Находясь в файле Excel, нажмите в верхнем меню кнопку fx. Затем, выберите среди функций тип "статистические", и из предложенного перечня в окошке - СТЬЮДРАСПОБР. Затем, по подсказке, поставив курсор в поле "вероятность" наберите значение обратной вероятности (т.е. в нашем случае вместо вероятности 0,95 надо набирать вероятность 0,05). Видимо, электронная таблица составлена так, что результат отвечает на вопрос, с какой вероятностью мы можем ошибиться. Аналогично в поле "степень свободы" введите значение (n-1) для своей выборки.

10.4. Центральная предельная теорема. Систематические изменения или случайность

Мы уже знаем, что нормальное распределение - особенное. Некоторые его свойства мы сможем использовать и для распределений, которые, строго говоря, нормальными не назовешь. Задача, которую мы рассмотрим в этом разделе имеет чрезвычайно важное значение для бизнеса, это задача о диагностировании тенденций к изменению показателей.

Удобство использование нормального распределения некоторых случайных величин и особые возможности, которые закон нормального распределения предоставляет исследователю, породили ряд теорем, которые позволяют пользоваться этими свойствами даже, если генеральная совокупность представляет собой "не вполне нормальное распределение".

Центральная предельная теорема имеет несколько формулировок, мы не будем их здесь полностью приводить и доказывать. Для нас важно знать только то, что в большинстве случаев среднее арифметическое выборки, взятой из генеральной совокупности (напомним, что это среднее арифметическое - тоже случайная величина), ложится на нормальное распределение гораздо лучше, чем исходная генеральная совокупность. Другими словами, если мы возьмем несколько выборок из генеральной совокупности, то средние арифметические величины этих выборок будут представлять собой новую случайную величину с практически нормальным распределением. Именно эта теорема и позволит нам проверять так называемые статистические гипотезы, т.е. делать заключение о наличии тенденции к изменению показателей деятельности, которые сами по себе, являясь случайными величинами, имеют право на некоторый разброс.

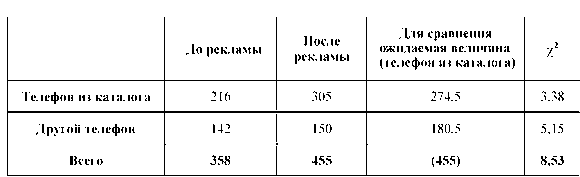
Пример. Фирма поместила информацию о своей продукции в каталоге. Был указан один из двух номеров телефона отдела продаж, на который и раньше поступали звонки потенциальных покупателей. Другой номер телефона в каталоге не упоминался. За два месяца до выхода каталога и в течение двух месяцев после было зарегистрировано следующее количество звонков на эти телефоны (два столбца в таблице). Как нам определить, подействовала ли информация, данная в каталоге, или мы имеем дело со случайным оживлением на рынке, а деньги на рекламу потрачены напрасно?

Последний столбец в таблице - ожидаемые величины. Это наши оценки, сделанные из предположения, что ничего не изменилось, и реклама не оказала никакого действия, т.е. произошло общее оживление на рынке и больше ничего, а пропорции между числом звонков на оба телефона должны сохраниться в точности. {Ожидаемая величина для телефона из каталога}=455ґ216/358=274,5 {Ожидаемая величина для другого телефона}=455ґ142/358=180,5. Наше предположение, о том, что реклама не оказала никакого воздействие на изменение числа покупателей, носит название нулевой гипотезы. Альтернативная гипотеза заключается в предположении о наличии такого влияния. Наша задача - выбрать более достоверную из двух этих гипотез. Чтобы оценить, насколько значимы отклонения реальной ситуации от ожидания по нулевой гипотезе, для обоих телефонов мы должны посчитать величину:

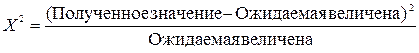
поставить их в таблицу и просуммировать.

Дальнейшие наши действия - определить, с какой вероятностью посчитанные отклонения "ложатся" на соответствующую кривую. Для такой оценки можно воспользоваться значениями X ² – критерия Пирсона. Обычно эти значения задаются в виде стандартных таблиц в книгах по статистике. Дадим и мы такую таблицу (X - греческая буква "хи"):

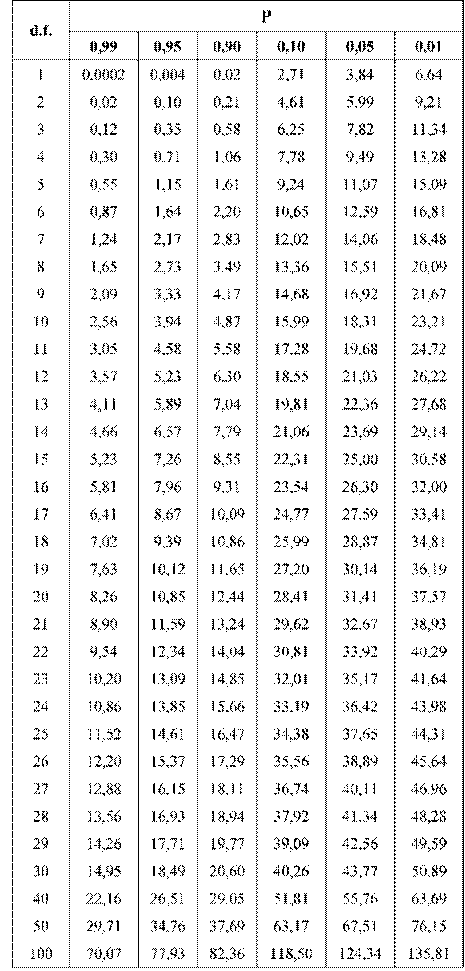
Теперь несколько слов о том, как пользоваться этой таблицей. Буквы d.f. означают число степеней свободы. Чтобы посчитать степени свободы нужно просто брать в таблице с исходными данными количество строк n и столбцов m, и посчитать величину (n-1)Ч(m-1). Это и будет количество степеней свободы в каждом конкретном случае. Правда, строки и столбцы берутся только для самих исходных данных, ни строка суммирования (всего), ни столбец подсчета ожидаемых величин при определении степени свободы не учитывается. В нашем случае d.f.=(2-1)Ч(2-1)=1, это означает, что степень свободы равна единице, и в таблице X ² мы должны пользоваться соответствующей строкой (верхней). Теперь о столбцах этой таблицы. Цифры 0,99; 0,95; и т.д. означают, что величины отклонений X ², стоящие в этих столбцах с вероятностью 0,99; 0,95; и т.д. возникли случайно. В нашем примере, вероятность случайного происхождения отклонения составляет менее 0,01 (т.е. меньше одного шанса из ста!). Мы вполне можем считать, что реклама оказала воздействие. Обратите внимание, что критерий X ²не говорит категорически, что случайность тут невозможна, просто вероятность этого очень мала. Другими словами, если мы отбросим нулевую гипотезу и выберем альтернативную, то вероятность ошибки будет меньше одного процента.

Если Вы будете пользоваться этим методом, совсем не нужно считать каждый раз вручную все отклонения. Подсчеты можно проводить в Excel автоматически. Сначала запишите известные Вам показатели в виде таблицы. Затем посчитайте в Excel столбец ожидаемых величин. После этого нажмите в верхнем меню кнопку f_x. Затем, выберите среди функций тип "статистические", и из предложенного перечня в окошке - ХИ2ТЕСТ. Затем, по подсказке, поставив курсор в поле "ожидаемый интервал" выделите мышью столбец ожидаемых значений (но не захватывайте сумму в нижней строке). Аналогично в поле "фактический интервал" введите массив из столбика фактических данных после рекламы. Программа сама посчитает граничную вероятность того, что отклонение было случайным. Так в нашем варианте более точное значение вероятности составляет примерно 0,0035. В таблице мы попали по значению X ²между столбцами и посчитать вероятность с такой точностью не смогли. Видимо для того, чтобы Вы привыкли пользоваться подобными оценками, имеет смысл обсудить вопрос о "степени свободы". Что это такое и какие степени свободы вообще могут быть? Понятно, что оценка значимости происходящих изменений может происходить только при наличии данных, как полученных при гипотетическом воздействии этих изменений, так и свободных от изменений. В качестве заведомо не подверженных изменениям данных в нашем примере выступали показания числа звонков на оба телефона до публикации каталога. Кроме того, для дополнительной объективности данных, мы использовали один телефон как неизвестный в рекламе. Это позволило нам исключить возможное влияние сезонных изменений спроса или другие подобные факторы. В других ситуациях, мы можем сравнивать динамику спроса на один товар с динамикой спроса на другой, если идет целевая раскрутка этого товара, или же товар входит в моду. И в этой ситуации свойства нормального распределения помогут нам сделать вывод о значимости происходящих изменений. После этого раздела Вам нужно будет выполнить третье письменное задание.

Дата добавления: 2013-12-12