Алгоритм построения плоскости, параллельной данной

Параллельные плоскости

Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости (рис. 6.1).

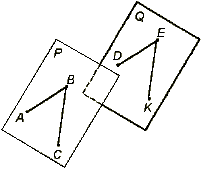
Рис. 6.1

Рассмотрим алгоритм построения плоскости, параллельной данной (табл. 6.1).

Необходимо построить плоскость Q, проходящую через точку D, параллельную данной плоскости Р(D АBC).

Таблица 6.1

Вербальная форма	Графическая форма
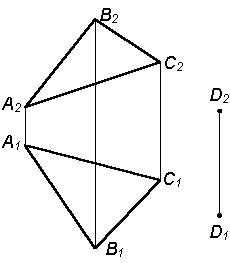
1. Для решения задачи в данной плоскости Р(D АBC) берутся любые пересекающиеся прямые. Например, АВ АС
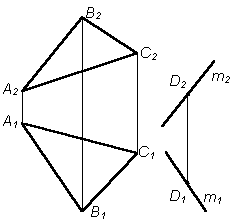
2. Через точку D проводим прямую m: m2 || A2B2; m2 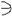D2 m1 || A1B1; m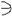1 D1
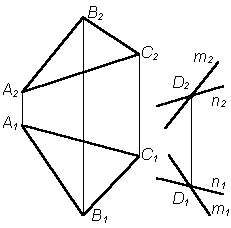
3. Через точку D проводим n || АС: n1 || А1С1; n2 || А2С2. Плоскость Q определяется двумя пересекающимися прямыми: Q (m n), так как эти две прямые параллельны двум пересекающимся прямым АВ и АС, плоскости Р и Q параллельны Р(D АВС) || Q (m n)

Дата добавления: 2013-12-12