Из двух и более компонентов

Равновесие в гетерогенных системах, состоящих

2.8.1 Равновесие жидкость – пар. Закон Рауля

Пусть в состоянии равновесия находятся жидкость и выделяющийся из нее пар. В соответствии с теоремой равновесия Гиббса химический потенциал любого компонента в системе одинаков во всех фазах:

.

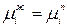Выразим химический потенциал i -го компонента в жидкой фазе через его термодинамическую активность, а в паровой фазе – через его парциальное давление, то есть примем, что паровая фаза идеальна. Тогда получим:

.

Преобразуем уравнение:

.

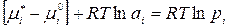Значение выражения, заключенного в скобки, найдем из граничного условия: если x_i = 1, то γ_i = 1, 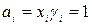и 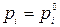,следовательно,

,

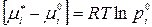где 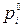– давление насыщенного пара над индивидуальным i- м компонентом при температуре раствора.

Подставим в уравнение вместо выражения в скобках его значение:

,

.

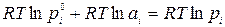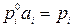Выразив активность через мольную долю и коэффициент активности, получим:

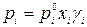, (2.8)

Уравнение (2.8) выражает основной закон жидких растворов – закон Рауля.

Применительно к идеальным жидким растворам (γ_i → 1) уравнение (2.8) запишется

.

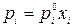Рассмотрим идеальный жидкий раствор, состоящий из летучих компонентов А и В, тогда:

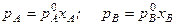
Выразим мольную долю компонента А через мольную долю компонента В:

х_А = 1 – х_В.

Общее давление над раствором складывается из парциальных давлений компонентов р = р_А + р_В, тогда

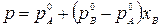
Таким образом, зависимость давления насыщенного пара компонентов и общего давления пара от состава раствора является линейной.

Зависимость давления насыщенного пара от состава двухкомпонентного раствора представляется в виде диаграммы р(р_А, р_В) – х (рис. 2.2).

Для описания зависимости давления насыщенного пара компонента от состава реального раствора используют закон Рауля в виде:

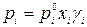
Для реального раствора, содержащего летучие компоненты А и В общее давление над раствором равно:

.

Рис. 2.2. Зависимость давления паров от состава раствора

Поскольку коэффициенты активности g_А и g_В зависят от состава раствора, то зависимость общего давления от состава раствора представляет собой кривую.

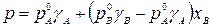Отклонения давления пара от линейной зависимости в сторону больших значений называют положительными, а в сторону меньших значений – отрицательными. Величина и вид отклонений зависят от сил взаимодействия между частицами. Силы взаимодействия межу частицами идеального раствора такие же, как и в чистых жидкостях, поэтому отклонений не возникает. В реальных растворах при уменьшении сил межмолекулярного взаимодействия усиливается испарение. Следовательно, увеличивается давление насыщенного пара и возникает положительное отклонение от линейной зависимости. Закономерности для растворов с отрицательными отклонениями имеют противоположный характер (рис. 2.3).

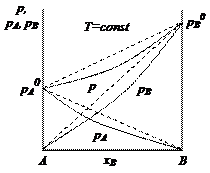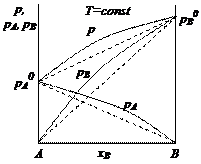а б

Рис. 2.3. Диаграмма состояния реальных растворов: а – с отрицательными отклонениями; б – с положительными отклонениями

Состав равновесного с жидким раствором пара (у_i) определяется согласно закону Дальтона:

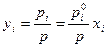– для идеального раствора;

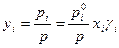– для реального раствора.

Для представления данных по фазовому равновесию жидкость-пар кроме рассмотренных диаграмм применяются также диаграммы давление пара – состав (р – х(у)), температура кипения – состав (Т – х(у)) и состав пара – состав раствора (y – x) (рис. 2.4).

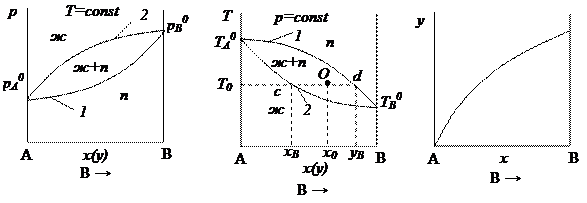Рис. 2.4. Диаграммы давление пара – состав (р – х(у)), температура кипения –

состав (Т – х(у)) и состав пара – состав раствора (y – x)

На представленных диаграммах:

точке А соответствует чистому компоненту А (100 %);

точке В – чистому компоненту В (100 %);

На диаграмме р – х(у):

1 – кривая зависимости давления насыщенного пара от состава пара;

2 – кривая зависимости давления насыщенного пара от состава жидкости.

Область ниже кривой состава пара отвечает состоянию гомогенной системы – пара; область выше кривой состава жидкости отвечает состоянию жидкости.

На диаграмме Т – х(у):

1 – кривая зависимости температуры кипения от состава пара;

2 – кривая зависимости температуры кипения от состава жидкости.

Область выше кривой состава пара отвечает состоянию гомогенной системы – пара; область ниже кривой состава жидкости отвечает состоянию жидкости.

Область, лежащая между кривыми состава пара и состава жидкости отвечает состоянию гетерогенной системы жидкость-пар, любая точка внутри этой области характеризует состояние равновесия между жидкостью и паром. Например, на диаграмме Т – х(у) в точке О при температуре Т ₀ находится гетерогенная система, состоящая из жидкости и пара общий состав которой равен х ₀. Точки с и d выражают составы равновесных жидкости х _В и пара у _В.

Таким образом, составы жидкости и равновесного с нею пара в общем случае неодинаковы.

Если известна масса гетерогенной смеси в точке О m, то по правилу рычага можно рассчитать массы равновесных фаз:

.

Дата добавления: 2013-12-11