Правило Крамера

Теория определителей имеет широкое применение в теории систем линейных уравнений.

Lemma

Сумма произведений элементов любой строки (столбца) на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

Доказательство.

Пусть дан определитель .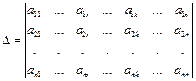

Габриэ́ль Кра́мер (31.07.1704 — 4.01.1752) — швейцарский математик, ученик и друг Иоганна Бернулли, один из создателей линейной алгебры. Заложил основы теории определителей. Ему принадлежат также исследования по теории алгебраических кривых высших порядков.

Рассмотрим другой определитель 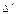, отличающийся от 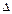только тем, что в k -ом столбце повторен i -ый столбец.

.

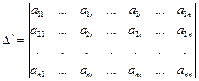По теореме 3.4 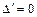. Разложим его по элементам k -го столбца, получим:

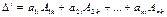, где 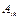- алгебраические дополнения к элементам k -го столбца определителя 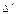. Но поскольку 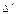отличается от 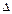только k -ым столбцом, то они будут и алгебраическими дополнениями элементов k -го столбца и в определителе 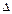. Таким образом.

.

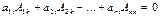
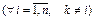Рассмотрим систему n линейных уравнений с n неизвестными:

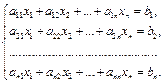(4.3)

Назовем определитель 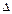матрицы СЛУ (4.3) главным определителем этой системы. Умножим первое уравнение на 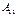, второе – на 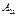и т.д., n-ое уравнение – на 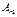и сложим их. Имеем:

.

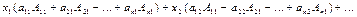
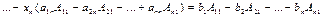Согласно выше доказанной лемме 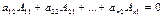, …, 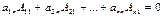. В силу следствия из теоремы Лапласа о разложении определителя по элементам столбц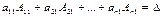а , а 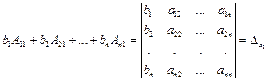- определитель, полученный из главного определителя СЛУ путем замены его первого столбца столбцом свободных членов. Таким образом, получили: 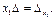(4.4)

Аналогично получаем: 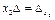, …, 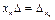(4.5)

1) Если 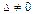, то СЛУ (4.3) имеет единственное решение:

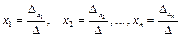
(4.6)

Формулы (4.6) называются формулами Крамера.

2) Если 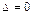, а хотя бы один из 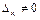, то СЛУ (4.3) несовместна.

3) Если 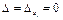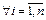, то СЛУ (3.9) неопределенна или несовместна.

Дата добавления: 2013-12-12