
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обратная матрица. Элементарные матрицы и их применение.
|
|
|
|
Нелинейные операции над матрицами
Def.Произведением строки 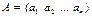 на столбец
на столбец 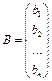 называется число равное
называется число равное 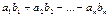 .
.
Заметим, что произведение строки и столбца определено, если они имеют одинаковую длину.
Def. Матрицы называют согласованными, если число столбцов первой матрицы равно числу строк второй матрицы.
Для согласованных матриц определяют их произведение.
Def.Произведениемматриц 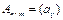 и
и 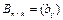 называется матрица
называется матрица 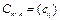 , где
, где
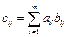 (5.6)
(5.6)
т.е. элемент 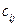 произведения определяется как произведение i -ой строки матрицы А на j -ый столбец матрицы В.
произведения определяется как произведение i -ой строки матрицы А на j -ый столбец матрицы В.


 N.
N. 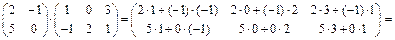
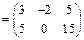 .
.
В примере акцентируется внимание на нахождении элемента 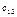 матрицы-произведения. Для этого перемножаются 1-я строка первого множителя на 2-й столбец второго множителя.
матрицы-произведения. Для этого перемножаются 1-я строка первого множителя на 2-й столбец второго множителя.
Свойства произведения матриц:
1. 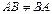 (произведение матриц не коммутативно);
2. (произведение матриц не коммутативно);
2. 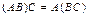 (ассоциативность произведения матриц);
3. (ассоциативность произведения матриц);
3. 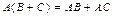 (дистрибутивность произведения матриц);
4. (дистрибутивность произведения матриц);
4. 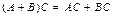 (дистрибутивность произведения матриц);
5. (дистрибутивность произведения матриц);
5. 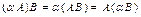 ;
6. ;
6. 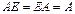 ;
7. ;
7. 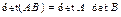 . .
|
Замечание. Эти свойства имеют место при условии, что все операции возможны.
Доказательство.
1. Для доказательства этого свойства достаточно привести контрпример.
Например, показать, что 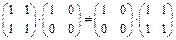 .
.
2. Пусть 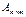 ,
, 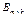 и
и 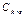 . Тогда
. Тогда 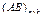 , а
, а 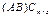 . С другой стороны,
. С другой стороны,
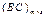 , а
, а 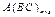 . Таким образом размерности матриц
. Таким образом размерности матриц 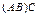 и
и 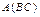 одинаковы. Обозначим
одинаковы. Обозначим 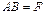 ,
, 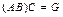 ,
, 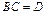 ,
, 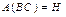 . Если теперь покажем, что
. Если теперь покажем, что 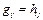 , то свойство доказано.
, то свойство доказано.
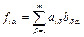 и
и 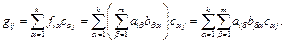
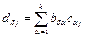 и далее
и далее 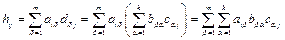 .
.
Заметим, что 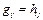 , т.к. они состоят из одних и тех же слагаемых, только расположенных в различном порядке
, т.к. они состоят из одних и тех же слагаемых, только расположенных в различном порядке  .
.
Идея доказательства свойств 3 – 6 прозрачна, а потому не приводим их.
В лекции 3 определялась операция транспонирования матрицы (формула 3.1). Эта операция носит общий характер, т.е. применима к любой матрице. Справедливы следующие свойства:
1. 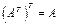 ;
2. ;
2. 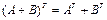 ;
3. ;
3. 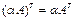 . где . где 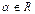 ;
4. ;
4. 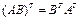 . .
|
Доказательство.
Свойства 1 – 3 проверяются непосредственно. Приведем доказательство свойства 4.
Пусть 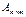 и
и 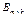 . Тогда
. Тогда 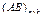 и
и 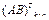 . С другой стороны,
. С другой стороны, 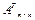 ,
, 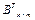 и
и 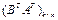 . Т.е. матрицы, стоящие в правой и левой частях равенства, имеют одинаковую размерность. Обозначим
. Т.е. матрицы, стоящие в правой и левой частях равенства, имеют одинаковую размерность. Обозначим 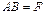 ,
, 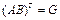 ,
, 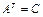 ,
, 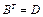 ,
, 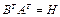 . Покажем, что
. Покажем, что 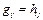 .
.
Имеем: 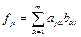 ,
, 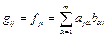 .
.
С другой стороны,
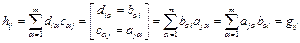 .
. 

|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 639; Нарушение авторских прав?; Мы поможем в написании вашей работы!