Группы. Кольца. Поля

НЕКОТОРЫЕ ОБЩИЕ ПОНЯТИЯ АЛГЕБРЫ. ПОЛЕ КОМПЛЕКСНЫХ ЧИСЕЛ. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОМПЛЕКСНЫХ ЧИСЕЛ.

В предыдущих лекциях речь шла о математических объектах, которые не являются числами, но над ними можно осуществлять алгебраические операции. Подобные системы объектов возникают в математике в различных ситуациях, потому возникает необходимость формализовать некоторые общие понятия.

Def. Говорят, что на множестве М определена бинарная операция 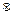, если для любых двух элементов 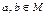определен элемент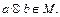

Def.Группой называется множество G, на котором определена некоторая бинарная операция 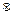(сложения или умножения) так, что выполняются условия:

1) 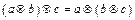(операция ассоциативна);

2) 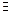нейтральный элемент 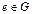такой, что ;

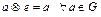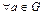
3) 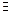обратный элемент 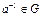такой, что .

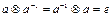Если групповая операция это операция сложения, группа называется аддитивной. В этом случае нейтральный элемент называют нулевым элементом.

Если групповая операция – умножение, то группу называют мультипликативной, а нейтральный элемент называют единичным.

Если для групповой операции справедлив коммутативный закон, то группу называют абелевой группой.

N. 1) Множество целых чисел Z – абелева аддитивная группа.

2) Множество чисел кратных а – абелева аддитивная группа.

3) Множество n-мерных векторов – абелева аддитивная группа.

4) Множество матриц размера 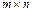- абелева аддитивная группа.

5) Множество невырожденных квадратных матриц одинаковой размерности – мультипликативная группа (не является абелевой. Почему?)

Def. Множество К, на котором определены операции сложения и умножения называется кольцом, если эти операции удовлетворяют следующим условиям:

1) ;

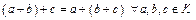2) 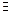нулевой элемент 0: ;

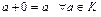3) 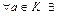противоположный элемент : ;

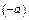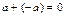4) ;

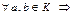
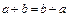5) ;

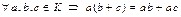6) .

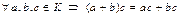Если к тому же 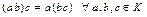, то кольцо 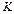называется ассоциативным. Если же 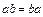, то кольцо 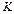называется коммутативным.

N. Множество квадратных матриц n-го порядка является ассоциативным кольцом.

Def. Коммутативное кольцо Р называется полем, если:

1) 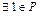(единичный элемент): ;

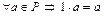2) 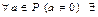обратный элемент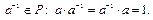

N. 1) Множество квадратных невырожденных матриц не является полем (Почему?).

2) Множество рациональных чисел Q и множество действительных чисел R являются полями.

Дата добавления: 2013-12-12