
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгебраическая форма записи комплексных чисел
|
|
|
|
Свойства операции над комплексными числами.
Поле комплексных чисел
Рассмотрим множества N, Z, Q, R. Рассмотрим уравнение вида 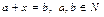 . В случае, если
. В случае, если 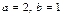 , то
, то 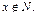 Таким образом, отыскание решений уравнения
Таким образом, отыскание решений уравнения 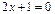 приводит к расширению множества N до множества Z.
приводит к расширению множества N до множества Z.
Рассмотрим уравнение 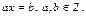 Решение уравнения
Решение уравнения 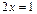 приводит к переходу к множеству Q. Аналогично решение уравнений
приводит к переходу к множеству Q. Аналогично решение уравнений 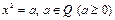 приводит к множеству R. Необходимость решать уравнение типа
приводит к множеству R. Необходимость решать уравнение типа 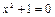 приводит к необходимости дальнейшего расширения множества чисел.
приводит к необходимости дальнейшего расширения множества чисел.
Поставим задачу построить новую систему чисел, которая бы содержала решения уравнения 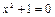 и являлась бы расширением множества R.
и являлась бы расширением множества R.
Def. Пару действительных чисел 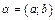 назовем комплексным числом.
назовем комплексным числом.
Для построения новой числовой системы необходимо определить основные операции над ее элементами:
1) 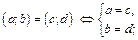 (8.1)
(8.1)
2) 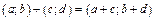 ; (8.2)
; (8.2)
3) 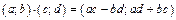 ; (8.3)
; (8.3)
Пусть 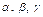 - комплексные числа. Тогда:
1. - комплексные числа. Тогда:
1. 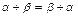 ;
2. ;
2. 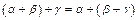 ;
3. ;
3. 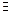 нулевой элемент нулевой элемент 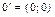 : : 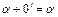 ;
4. ;
4. 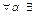 противоположный элемент противоположный элемент 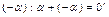 ;
5. ;
5. 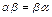 ;
6. ;
6. 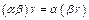 ;
7. ;
7. 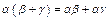 ;
8. ;
8. 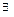 единичный элемент единичный элемент 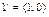 : : 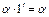 ;
9. ;
9. 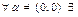 обратный элемент обратный элемент 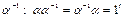 . .
|
Доказательство.
Свойства 1-3, 5 очевидны, они вытекают непосредственно из определения операций сложения и умножения комплексных чисел. Докажем остальные свойства.
Свойство 4. Пусть 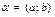 , тогда
, тогда 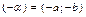 . Действительно,
. Действительно, 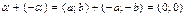
 .
.
Свойство 6. Пусть 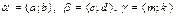 .
.
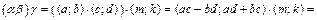
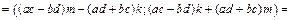
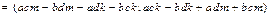 .
.
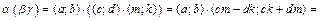
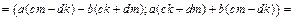
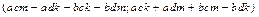 .
.
Значит, 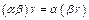
 .
.
Свойство 7. Доказывается аналогично свойству 6.
Свойство 8. Докажем, что существует единственный единичный элемент 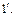
Необходимо найти такой элемент 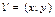 , что
, что 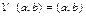 .
.
Имеем 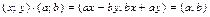 . Отсюда получаем систему линейных уравнений:
. Отсюда получаем систему линейных уравнений:
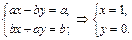
Значит, 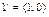 - единственный единичный элемент
- единственный единичный элемент  .
.
Свойство 9. Найдем обратный элемент 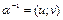 для
для 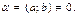
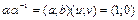 . Отсюда:
. Отсюда:
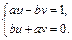
Решим полученную СЛУ по формулам Крамера. 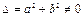 (т.к.
(т.к. 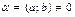 ),
), 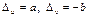 . Имеем,
. Имеем,
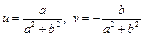 .
.
Значит, 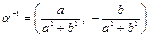
 .
.
Def. Под разностью комплексных чисел 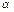 и
и 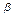 будем понимать комплексное число, которое получается следующим образом:
будем понимать комплексное число, которое получается следующим образом:
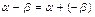 (8.4)
(8.4)
Т.к. для каждого комплексного числа 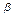 противоположный элемент
противоположный элемент 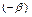 определен однозначно, то и операция вычитания определена однозначно.
определен однозначно, то и операция вычитания определена однозначно.
Def. Число 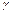 называют частным от деления числа
называют частным от деления числа 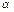 на число
на число 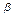 , если
, если 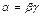 .
.
Пусть 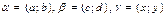 . Тогда
. Тогда
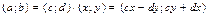 .
.
Составим систему уравнений: 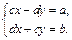
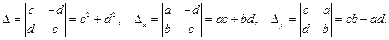
Система будет иметь единственное решение, если 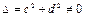 , т.е
, т.е 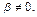 В этом случае
В этом случае
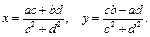
Таким образом, получаем
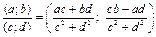 (8.5)
(8.5)
Нетрудно проверить, что 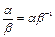 (сделайте это самостоятельно).
(сделайте это самостоятельно).
Итак, определены основные операции на множестве комплексных чисел и, следовательно, завершено построение системы комплексных чисел. Свойства введенных операций над комплексными числами позволяют сделать вывод о том, что множество комплексных чисел является полем. Поле комплексных чисел обозначают большой латинской буквой С.
Проверим действие введенных операций на множестве действительных чисел. Пару 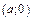 отождествим с действительным числом
отождествим с действительным числом 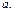 Применим к
Применим к 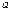 и
и 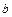 те арифметические операции, которые были определены на множестве комплексных чисел. Из (8.2 – 8.5) получаем:
те арифметические операции, которые были определены на множестве комплексных чисел. Из (8.2 – 8.5) получаем:
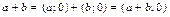 ;
;
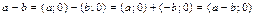
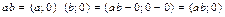
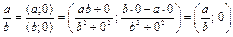 .
.
Таким образом, применение операций на множестве С дает те же результаты, что и соответствующие операции на R. Следовательно С есть алгебраическое расширение множества R.
Обозначим 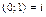 . Тогда
. Тогда 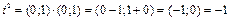 .
.
Таким образом, число i является корнем уравнения 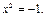
Перейдем к другой, более удобной форме записи комплексных чисел. Очевидно, 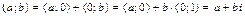 .
.
Def. Если комплексное число 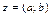 записано в виде
записано в виде 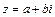 , то такую форму записи называют алгебраической формой записи комплексного числа.
, то такую форму записи называют алгебраической формой записи комплексного числа.
Число i называют мнимой единицей, 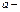 действительной частью числа z
действительной частью числа z 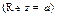 ,
, 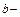 мнимой частью числа z
мнимой частью числа z 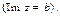 Числа вида
Числа вида 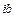 называют чисто мнимыми числами.
называют чисто мнимыми числами.
Def. Пусть 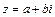 . Числом, сопряженным z, называется число
. Числом, сопряженным z, называется число 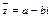
Операции 8.2 - 8.5 определяются для комплексных чисел, записанных в алгебраической форме следующим образом:
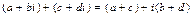 ; (8.6)
; (8.6)
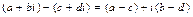 ; (8.7)
; (8.7)
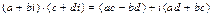 ; (8.8)
; (8.8)
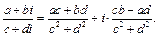 (8.9)
(8.9)
| Символ i для мнимой единицы предложил Л. Эйлер в 1777, взявший для этого первую букву слова лат. imaginarius. Ему же принадлежит мысль об алгебраической замкнутости поля комплексных чисел (1751), но строгое доказательство этого факта принадлежит Гауссу (1799). Гаусс и ввёл в широкое употребление термин «комплексное число» в 1831 году, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году. |
Нет необходимости запоминать эти формулы. Можно заметить, что достаточно лишь раскрыть скобки и привести подобные слагаемые относительно действительных и мнимых частей. При умножении комплексных чисел, записанных в алгебраической форме, следует формально перемножить выражения (как двучлен на двучлен), учитывая, что 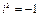 , а затем выделить действительную и мнимую части полученной суммы.
, а затем выделить действительную и мнимую части полученной суммы.
Выполнение операции деления легко формализуется, если предварительно числитель и знаменатель умножить на число сопряженное с числителем. Действительно,
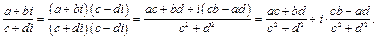
N. 1) 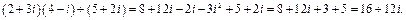
2) 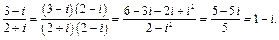
| Th.8.1 | (свойства операции сопряжения)
1. 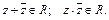 2.
2. 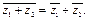 3.
3. 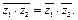 4.
4. 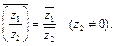
|
Доказательство.
1. 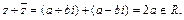
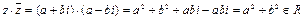
 .
.
2. 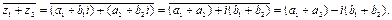
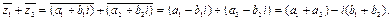
Таким образом, 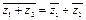
 .
.
3. 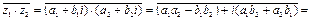
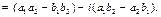
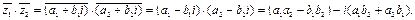
Таким образом, 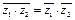
 .
.
4. 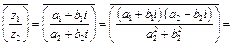
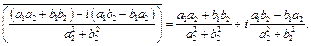
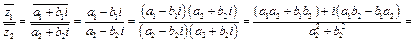
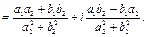
Таким образом, 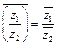
 .
.
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 1112; Нарушение авторских прав?; Мы поможем в написании вашей работы!