
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Базис, координаты вектора
|
|
|
|
Линейная зависимость (независимость) векторов.
Линейная зависимость (независимость) геометрических векторов определяется также, как и для векторов n -мерного векторного пространства (см. лекцию 7).
| Th.10.1 | Два вектора коллинеарны тогда и только тогда, когда они линейно зависимы. |
Доказательство.
Если один из векторов нулевой, то утверждение теоремы очевидно. Поэтому далее предполагаем, что оба вектора ненулевые.
Пусть  и
и 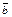 – коллинеарны. Отложим их от одной точки. Пусть
– коллинеарны. Отложим их от одной точки. Пусть 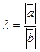 . Тогда если
. Тогда если 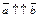 , то
, то 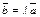 , если
, если 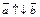 , то
, то 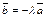 . В обоих случаях
. В обоих случаях  и
и 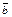 – линейно зависимы.
– линейно зависимы.
Пусть  и
и 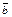 – линейно зависимы, т.е.
– линейно зависимы, т.е. 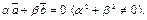 Тогда
Тогда 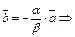
 и
и 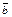 – коллинеарны
– коллинеарны  .
.
Следствия. Если  и
и 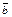 – коллинеарны и
– коллинеарны и 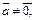 то
то 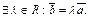
| Th.10.2 | Три вектора компланарны тогда и только тогда, когда они линейно зависимы. |
Доказательство.
Будем предполагать, что никакие два из них не коллинеарны, т.к. иначе доказательство очевидно (свойство линейно зависимых векторов).
Пусть 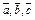 компланарны. Отложим их от точки O. Проведем через концы вектора компланарны. Отложим их от точки O. Проведем через концы вектора 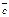 прямые, параллельные векторам прямые, параллельные векторам  и и 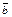 и рассмотрим параллелограмм и рассмотрим параллелограмм 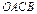 (рис. 10.10) (рис. 10.10)
| 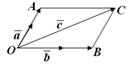 Рис. 10.10
Рис. 10.10
|
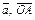 - коллинеарны
- коллинеарны 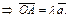 Аналогично,
Аналогично, 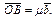 Тогда:
Тогда:
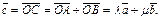
Значит, 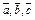 линейно зависимы.
линейно зависимы.
Пусть 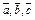 – линейно зависимы. Тогда
– линейно зависимы. Тогда 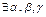 , одновременно не равные нулю:
, одновременно не равные нулю:  Если, например,
Если, например, 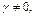 то
то 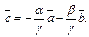 Тогда,
Тогда, 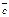 направлен вдоль диагонали параллелограмма со сторонами, вдоль которых направлены векторы
направлен вдоль диагонали параллелограмма со сторонами, вдоль которых направлены векторы  и
и 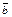 , т.е
, т.е 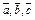 лежат в одной плоскости, а, значит, компланарны
лежат в одной плоскости, а, значит, компланарны  .
.
| Th.10.3 | Любые четыре вектора линейно зависимы. |
Доказательство.
Предположим, что никакие три вектора некомпланарны, иначе утверждение теоремы очевидно. Через точку D проведем три плоскости, параллельные парам векторов  и
и 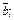
 и
и 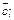
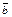 и
и 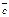 (рис. 10.11). По аналогии с теоремой 10.2 имеем:
(рис. 10.11). По аналогии с теоремой 10.2 имеем:
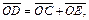
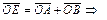
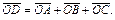 Таким образом,
Таким образом,
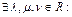 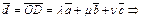 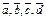 – линейно зависимы – линейно зависимы  .
Следствие. Любой вектор в пространстве может быть разложен по трем некомпланарным векторам, т.е. представлен в виде их линейной комбинации.
Def. Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов. .
Следствие. Любой вектор в пространстве может быть разложен по трем некомпланарным векторам, т.е. представлен в виде их линейной комбинации.
Def. Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
|
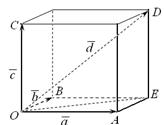 Рис. 10.11
Рис. 10.11
|
Def. Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов.
Пусть задан некоторый базис 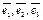 . Тогда любой вектор
. Тогда любой вектор  может быть разложен по этому базису, т.е. представлен в виде
может быть разложен по этому базису, т.е. представлен в виде
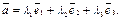 (10.9)
(10.9)
Def. Коэффициенты этого разложения 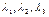 называют координатами вектора
называют координатами вектора  . Пишут
. Пишут 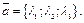
Очевидно, что 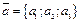 и
и 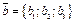 равны тогода и только тогда, когда
равны тогода и только тогда, когда 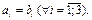
| Th.10.4 | Если 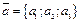 и и 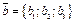 , то:
1. , то:
1. 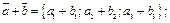 2.
2. 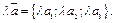
|
Доказательство вытекает непосредственно из формулы (10.9) и свойств линейных операций над векторами.
Замечание. Очевидно, что между множеством векторов и множеством векторов пространства 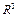 можно установить взаимно однозначное соответствие. Поэтому все утверждения, касающиеся векторов n-мерного векторного пространства можно перенести на геометрические вектора.
можно установить взаимно однозначное соответствие. Поэтому все утверждения, касающиеся векторов n-мерного векторного пространства можно перенести на геометрические вектора.
N. Убедиться, что векторы 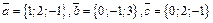 образуют базис. Разложить вектор
образуют базис. Разложить вектор 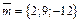 по этому базису.
по этому базису.
Решение.
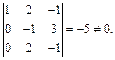
Таким образом, строки определителя линейно независимы, а значит, векторы линейно независимы, т.е. образуют базис. Представим вектор 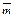 в виде линейной комбинации векторов
в виде линейной комбинации векторов 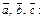
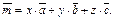
Подставим в данное соотношение координаты векторов 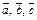 и
и 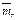 записав их для удобства как вектор-столбцы:
записав их для удобства как вектор-столбцы:
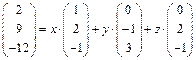
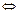
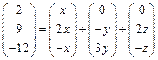
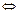
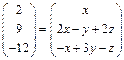
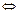
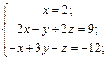
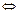
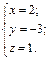
Значит, 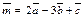 – искомое разложение.
– искомое разложение.
Ответ: 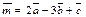
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 737; Нарушение авторских прав?; Мы поможем в написании вашей работы!