
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прямолинейные образующие поверхностей второго порядка
|
|
|
|
Некоторые из рассмотренных поверхностей второго порядка можно образовать движением одной прямой. Это очевидно для цилиндра и конуса. Оказывается, что однополостной гиперболоид и гиперболический параболоид также являются поверхностями, состоящими из прямолинейных образующих.
Рассмотрим однополостной гиперболоид, заданный своим каноническим уравнением
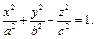 (18.21)
(18.21)
Перепишем его в виде
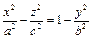
или
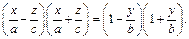 (18.22)
(18.22)
Рассмотрим прямую
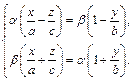 (18.23)
(18.23)
Если координаты некоторой точки 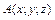 удовлетворяют уравнениям (18.23), то ее координаты очевидно удовлетворяют и (18.22). Значит, соотношение (18.23) задает семейство прямых, лежащих на однополостном гиперболоиде.
удовлетворяют уравнениям (18.23), то ее координаты очевидно удовлетворяют и (18.22). Значит, соотношение (18.23) задает семейство прямых, лежащих на однополостном гиперболоиде.
Покажем теперь, что через любую точку однополостного гиперболоида проходит некоторая прямая семейства (18.23). Пусть точка 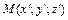 принадлежит однополостному гиперболоиду, тогда
принадлежит однополостному гиперболоиду, тогда
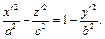 (18.24)
(18.24)
Выберем 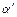 и
и 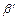 так, чтобы
так, чтобы
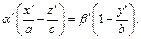 (18.25)
(18.25)
Докажем, что 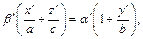 т.е. что точка
т.е. что точка 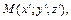 принадлежащая однополостному гиперболоиду, принадлежит также прямой, определяемой уравнениями (18.23). Пусть
принадлежащая однополостному гиперболоиду, принадлежит также прямой, определяемой уравнениями (18.23). Пусть
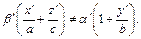 (18.26)
(18.26)
Из (18.25) и (18.26) следует, что 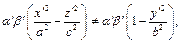 что противоречит соотношению (18.23).
что противоречит соотношению (18.23).
Def. Прямые (18.22) называют прямолинейными образующими однополостного гиперболоида (рис. 18.11).
Рассмотрим теперь гиперболический параболоид, заданный своим каноническим уравнением
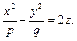 Переписав это уравнение в виде
Переписав это уравнение в виде
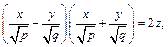 заметим, что любая прямая, определяемая уравнениями
заметим, что любая прямая, определяемая уравнениями
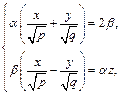 (18.27) (18.27)
| 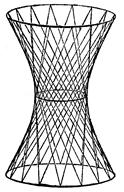 Рис. 18.11
Рис. 18.11
|
или
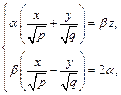 (18.28)
(18.28)
при любых, не равных одновременно нулю значениях 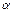 и и 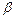 целиком располагаются на гиперболическом параболоиде (рис. 18.12).
Def. Прямые (18.27) и (18.28) называются прямолинейными образующими гиперболического параболоида. целиком располагаются на гиперболическом параболоиде (рис. 18.12).
Def. Прямые (18.27) и (18.28) называются прямолинейными образующими гиперболического параболоида.
| 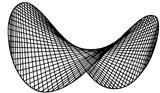 Рис. 18.12
Рис. 18.12
| |

| Идея использования линейчатого характера однополостного гиперболоида в строительной технике принадлежит русскому инженеру В.Г. Шухову (1853—1939). Роль прямолинейных образующих играют железобетонные или металлические балки. Такие конструкции оказались легкими и прочными, поскольку каждая образующая в нескольких местах соединена с другими образующими. В 1920-1922 гг. в | |
г. Москва по проекту В. Г. Шухова была построена радиовышка на Шаболовке высотой около 150 м. Башня получила признание как одно из самых красивых и выдающихся достижений инженерной мысли в мире.
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 347; Нарушение авторских прав?; Мы поможем в написании вашей работы!