Дифференциальные уравнения плоско-параллельного движения твердого тела

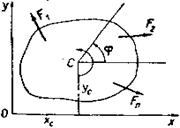
Как известно из кинематики (ч.II., гл. V, § 3), плоско-параллель­ное движение твердого тела определяется тремя независимыми параметрами: координатами х_c и у_c полюса (который выберем в центре инерции С тела) и углом поворота φ тела вокруг центра инерции (рис. 118). Следовательно, в данном случае тело имеет три степени свободы (k = 3). Поэтому составим три уравнения Лагранжа второго рода

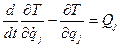(j=1,2,3).

Будем рассматривать координаты х_c, у_c и угол по­ворота φ, как обобщенные координаты: q₁=x_c, q₂=y_c, q₃= φ

Пусть к телу приложена система сил F₁, F₂,…,F_n указанная на рис. 118. Вычислим обобщенные силы

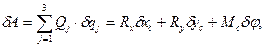
где R_x, R_y — проекции главного вектора приложенных к телу внешних сил F _iна координатные оси Ох и Оу, а М_c — главный момент этих сил относительно оси С_z,перпендикулярной к плоскости движения.

Обобщенные силы соответственно равны

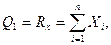
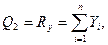
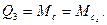
Кинетическая энергия тела согласно формуле (111.121) равна

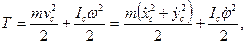
где m — масса тела, I_c-его момент инерции относительно центральной оси С_z.

Вычисляя частные производные 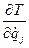и 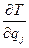и подставляя в урав-

нения Лагранжа второго рода, получим искомые дифференциальные уравнения плоско-параллельного движения твердого тела

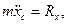
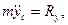
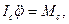
или в векторной форме

m r _c= R, I _c ε = M _c,

где ε=φ — угловое ускорение тела, г_c = ω_c — ускорение центра масс тела,

М_c — главный момент относительно точки С.

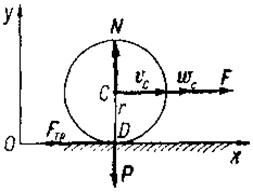
П р и м е р. Колесо радиуса г и веса Р катится без сколь­жения по горизонтальной плоскости под действием силы F, приложенной в центре инерции колеса (рис. 119). Задан закон движения центра инерции колеса х_c =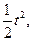, у_c = г.

Найти величину силы F, нормальную реакцию опоры N и коэффициент трения k колеса о плоскость.

Произведем анализ сил, действующих на колесо. На него действует сила F, сила тяжести Р и реакция горизонтальной плоскости, состоящая из нормальной реакции N и силы тре­ния F_тр, которая направлена в сторону, противоположную движению колеса.

Применив уравнения (111.226), получим

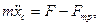
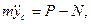
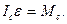
Так как

x_c=1, y_c=0, F_тр=kN, M_c=-F_трr=-kNr,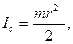

то

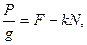N=P,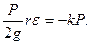

Мгновенный центр скоростей тела находится в точке касания колеса с плос­костью движения. Поэтому

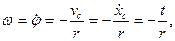
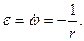
Таким образом,

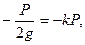
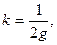
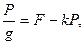
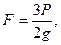N=P,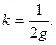

Дата добавления: 2013-12-12