Об интегрировании динамических уравнений Эйлера

Дифференциальные уравнения вращательного движения твердого тела вокруг неподвижной точки (динамические уравнения Эйлера)

Для вывода дифференциальных уравнений вращательного дви­жения твердого тела вокруг неподвижной точки воспользуемся уравнениями Лагранжа второго рода

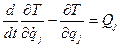(j=1,2,…,λ).

и совместим подвижные координатные оси Oξ, Oη, Oζ неизменно связанные с телом, с его главными осями инерции относительно неподвижной точки О.

Из кинематики известно (ч. II, гл. VI, § 2), что положение твер­дого тела с неподвижной точкой определяется тремя углами Эйлера, которые примем за обобщенные координаты

q₁=ψ, q₂= θ, q₃=φ.

Тело в рассматриваемом случае имеет три степени свободы (k = 3).

В соответствии с формулами (111.118), кинетическая энергия тела равна

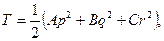
где А =I_ξ, В =I_η, С=I_ζ - главные моменты инерции тела от­носительно подвижных осей, р=ω_ξ, q=ω_η, r=ω_ζ -проекции угловой скорости вращения тела на подвижные оси, определяемые из кинематических уравнений Эйлера

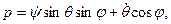
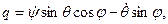
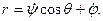
Вычислим частные производные

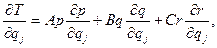
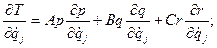
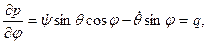
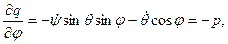
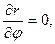
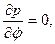
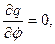
так что

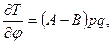
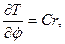
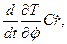
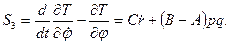
Аналогично получим:

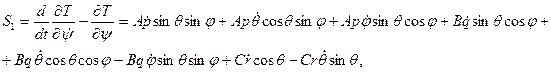
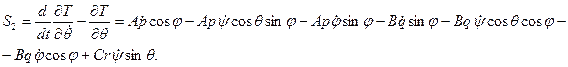
В соответствии с теоремой Эйлера о перемещении тела с неподвиж­ной точкой (ч. II, гл. VI, § 1)

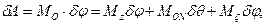
следовательно, обобщенные силы соответственно будут

Q₁=M_z, Q₂=M_ON, Q₃=M_ζ,

где M_z, M_ON, M_ζ— главные моменты приложенных к телу внешних сил относительно неподвижной оси О_z, линии узлов ОN и подвижной оси O_ζ.

Таким образом, уравнения Лагранжа второго рода в рассматри­ваемом случае будут

S₁=M_z, S₂=M_N, S₃=M_ζ.

Из трех полученных дифференциальных уравнений первые два очень громоздкие, в то время как третье уравнение

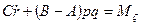
имеет чрезвычайно простую, симметричную форму и оно явно не со­держит компоненты угловой скорости тела p,q,r. Очевидно, слож­ность записи первых двух уравнений объясняется тем, что в правых частях этих уравнений вместо моментов М_ξ, М_η фигурируют

отличные от них обобщенные силы М_z и М_N. Однако путем надлежа­щего преобразования г эти уравнения можно привести к форме, аналогичной третьему уравнению.

Итак, дифференциальные уравнения вращательного движения твердого тела вокруг неподвижной точки принимают вид

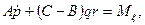
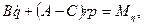
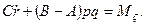
Эти уравнения называются динамическими уравнениями Эйлера. Заметим, что уравнения Эйлера можно также вывести, применив теорему об изменении кинетического момента.

Общий случай решения задачи о вращении твердого тела вокруг неподвижной точки и, следовательно, решение системы (111.228) и (11.113) дифференциальных уравнений связан с непреодолимыми математическими трудностями. В наиболее простых случаях, когда действующие на тело внешние силы либо приводятся к равнодей­ствующей, линия действия которой проходит через неподвижную точ­ку, либо имеют равный нулю главный момент относительно непо­движной точки, уравнения (111.228) принимают вид

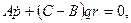
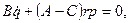
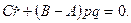
допускают два первых интеграла

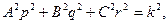
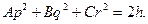
Один из этих интегралов получим, если первое из уравнений умножим на р, второе — на q, а третье — на r и результаты сложим;

Преобразование, о котором идет речь, имеет весьма сложный вид:

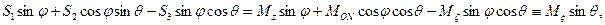
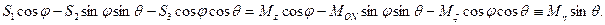
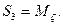
Предлагаем читателю убедиться в том, что каждое из написанных уравне­ний совпадает с соответствующим уравнением (111.228). При этом следует обра­титься к рис. 81, имея в виду, что

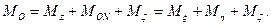
Рис. 120

для получения второго интеграла нужно первое из уравнений умно­жить на Ар, второе — на Вq, третье — на Сr и сложить эти произве­дения. Можно показать, что произвольные постоянные, входящие в эти интегралы, имеют простое механическое истолкование, а именно: постоянная k представляет собой абсо­лютную величину кинетического момента отно­сительно неподвижной точки (k = L₀), а по­стоянная h равна, кинетической энергии те­ла (h=T).

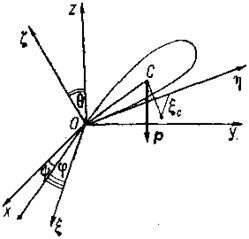
Практический интерес представляет случай, когда твердое тело вращается вокруг непо­движной точки под действием силы тяжести (рис. 120).

Обозначим координаты центра тяжести С в подвижной системе координат ξ_c, η_c, ζ_c. Про­екции силы тяжести Р на подвижные оси име­ют вид

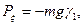
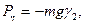
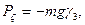
где

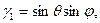
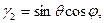
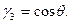
Если обозначить радиус-вектор точки С через г _c, а орты подвижных осей через i, j, k, то момент силы тяжести относительно неподвижной точки О будет

M _O(P)= r _c× P =-mg

и, следовательно, моменты силы Р относительно подвижных осей:

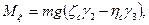
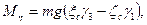
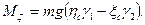
Подставляя эти выражения в уравнения (111.228), получим ди­намические уравнения Эйлера для случая, когда тело вращается вокруг неподвижной точки под действием силы тяжести:

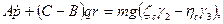
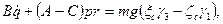
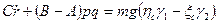
В настоящем курсе не рассматривается вопрос об интегрировании динамических уравнений Эйлера. Заметим лишь, что трудности

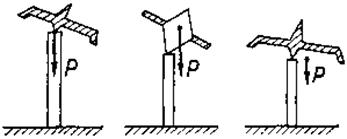
Случай Эйлера Случай Случай

Логранж Корейской

связанные с решением этого вопроса, привели исследователей к рассмотрению частных случаев движения тела вокруг неподвижной точки. Л. Эйлер рассмотрел случай, когда тело под действием силы тяжести вращается вокруг неподвижной точ­ки, совпадающей с центром тяжести тела; Лагранж,— когда

А = В и центр тяжести тела лежит на оси симметрии, проходящей через неподвижную точку. С. В. Ковалевская ис­следовала случай, когда А=В = 2С, а центр тяжести тела находится в экваториальной плоскости эллипсоида инерции.Эти случаи про­иллюстрированы на рис. 121, принадлежащем Н. Е. Жуков­скому. Теория вращательного движения твердого тела вокруг непод­вижной точки получила большое развитие в теории гироскопов, ши­роко применяемых в современной технике.

Пример. Рассмотрим случай регулярной прецессии. Этот случай движения тела вокруг неподвижной точки будет иметь место в приближенной теории гироскопа.

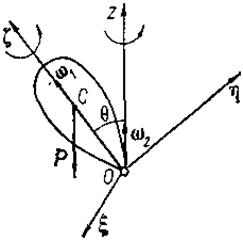
Пусть твердое тело имеет материальную ось симметрии ζ, вокруг которой оно вращается с постоянной по величи­не угловой скоростью ω₁, а ось ξ в свою очередь вращается вокруг неподвижной оси г (рис. 122) с угловой скоростью шз, причем ось образует с z постоянный угол нутации θ. Движе­ние тела, при котором соблюдаются указанные выше усло­вия, называется регулярной прецессией, а ω₂ — угловой ско­ростью регулярной прецесии. Тогда кинематические формулы Эйлера (11.113) примут вид:

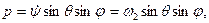
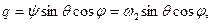
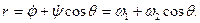
В силу симметрии А=В. Поэтому из третьего уравнения (111.228) найдем

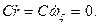
откуда

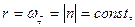
следовательно,

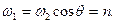
По (111.212) найдем

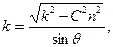
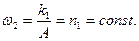
Интегрируя эти уравнения, найдем углы Эйлера, т. е. определим вращение тела вокруг неподвижной точки при высказанных предположениях:

θ=const,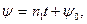

где n₂ — постоянная; φ₀, ψ₀ — значения углов φ и ψ в момент t = 0. Таким образом, в случае регулярной прецессии угол нутации 6 остается постоянным, а угол прецессии ψ и угол собственного вращения φ изменяются пропорцио­нально времени.

Дата добавления: 2013-12-12