Дифференциальные уравнения движения свободного твердого тела

Пусть свободное твердое тело движется под действием приложен­ных к нему сил F₁, F₂,…,F_n. Требуется определить движение этого тела относительно неподвижной системы координат Охуz. Начало подвижной системы координат Сξηζ поместим в центре инерции (центре тяжести) С тела и предположим, что подвижная система координат относительно неподвижной движется поступательно.

Из кинематики известно (ч. II, гл. VII, § 1), что движение свобод­ного твердого тела может быть разложено на поступательное вместе с произвольно выбранным полюсом и мгновенно вращательное во­круг полюса. В качестве полюса выберем центр инерции тела. Следо­вательно, при определении движения свободного твердого тела под влиянием приложенных к нему сил сначала нужно определить дви­жение его центра инерции, а затем мгновенно вращательное движение относительно центра инерции, рассматривая его как неподвижную точку и применяя при этом теорию вращательного движения тела во­круг неподвижной точки под действием указанных выше внешних сил.

Таким образом, на основании (111.217) и (111.228) дифференциаль­ные уравнения движения свободного твердого тела примут вид

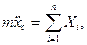
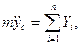
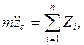
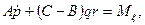
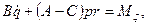
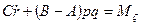
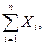
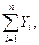
где т — масса тела; 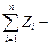проекции главного вектора приложенных к телу внешних сил на неподвижные координатные оси; х_c, у_c, r_c — проекции ускорения центра инерции тела на эти же оси; p, q, r — проекции мгновенной угловой скорости вращения тела вокруг центра инерции на подвижные оси, неизменно связан­ные с телом и являющиеся его главными осями инерции относитель­но центра инерции; А, В, С — главные моменты инерции тела от­носительно подвижных осей; М_ξ, М_η, М_ζ — главные моменты при­ложенных к телу внешних сил относительно подвижных осей.

Уравнения (III. 233) представляют собой систему шести дифферен­циальных уравнений, из которых можно определить шесть неизвест­ных функций

x_c=x_c(t), y_c=y_c(t), z_c=z_c(t); p=p(t), q=q(t), r=r(t).

Для определения углов Эйлера ψ=ψ(t), θ=θ(t), φ=φ(t) нужно воспользоваться кинематическими уравнениями Эйлера (П.113). При интегрировании всех указанных уравнений нужно учитывать начальные условия движения свободного твердого тела.

Гироскопом называется тело вращения, имеющее ось материаль­ной симметрии и вращающееся вокруг этой оси.

Осью материальной симметрии называется геометрическая ось симметрии тела, на которой расположены центры тяжести элемен­тов тела, симметричных относительно оси. Центр инерции (центр тяжести) С гироскопа находится на оси материальной симметрии, являющейся главной центральной осью инерции. Для гироскопов характерным является наличие неподвижной точки. Ось гироскопа в одной точке чаще всего крепится с помощью рамок. Неподвижная точка гироскопа находится в точке пересечения оси гироскопа с осями вращения рамки.

Гироскопы бывают с двумя и тремя степенями свободы. Ограни­чимся рассмотрением гироскопов с тремя степенями свободы. Ока­зывается, если к точкам материальной оси симметрии гироскопа при­ложить силы, стремящиеся изменить направление этой оси, то воз­никают явления, приближенная теория которых рассматривается в этой главе.

Исследование движения гироскопов с помощью динамических уравнений Эйлера очень сложно в связи с возникающими при этом математическими трудностями.

Дата добавления: 2013-12-12