Кинетическая энергия

Л Е К Ц И Я № 5. К И Н Е Т И Ч Е С К А Я Э Н Е Р Г И Я,

Потенциальная энергия тела в однородном поле силы тяжести Земли

Формула (15) справедлива также для однородных сферических тел; в этом случае r – расстояние между центрами масс таких тел. В частности, потенциальная энергия тела массы т, находящегося в поле гравитации Земли, масса которой М,

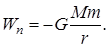(16)

Изменение потенциальной энергии тела массы m, поднятого с поверхности Земли (r = R, где R – радиус Земли)на высоту h (r = R + h), согласно (16), равно:

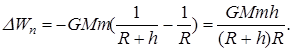(17)

Если h<<R, то в знаменателе формулы (17) можно пренебречь слагаемым h и она перейдет в известную формулу

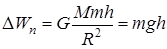или 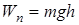, (18)

если потенциальную энергию на поверхности Земли принять равной нулю, где 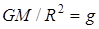– ускорение силы тяжести на поверхности Земли. Таким образом, формула (18) была получена в предположении, что сила тяжести (и ускорение силы тяжести) не изменяются с высотой h, т.е. поле силы тяжести Земли однородно. Поэтому формула (18) является приближенной формулой, в отличие от строгой формулы (16).

З А К О Н С О Х Р А Н Е Н И Я Э Н Е Р Г И И

Напишем уравнение движения материальной точки (частицы) массы m, движущейся под действием сил, результирующая которых равна : .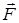

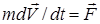Умножим скалярно правую и левую часть этого равенства на элементарное перемещение точки 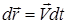, тогда

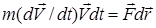. (1)

Так как 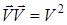, то легко показать, что 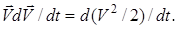Используя последнее равенство и то обстоятельство, что масса материальной точки постоянная величина, преобразуем (1) к виду .

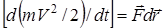Проинтегрировав части этого равенства вдоль траектории частицы от точки 1 до точки 2, имеем:

.

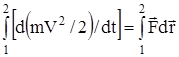Согласно определению первообразной и формуле (4.3) для работы переменной силы, получим соотношение: .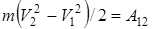

Величина

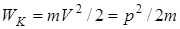(2)

называется кинетической энергией материальной точки.

Таким образом мы приходим к формуле

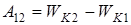, (3)

из которой следует, что работа результирующей всех сил, действующих на материальную точку, расходуется на приращение кинетической энергии этой частицы.

Полученный результат без труда обобщается на случай произвольной системы материальных точек.

Кинетической энергией системы называется сумма кинетических энергий материальных точек, из которых эта система состоит или на которые ее можно мысленно разделить: .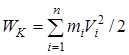

Напишем соотношение (3) для каждой материальной точки системы, а затем все такие соотношения сложим. В результате снова получим формулу, аналогичную (3), но для системы материальных точек.

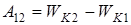, (4)

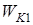где и 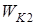– кинетические энергии системы, а под 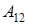необходимо понимать сумму работ всех сил, действующих на материальные точки системы.

Таким образом мы доказали теорему (4): работа всех сил, действующих на систему материальных точек, равна приращению кинетической энергии этой системы.

Дата добавления: 2013-12-12