Вычисление обратных матриц

Вычисление определителей высоких порядков

В отличие от технологии вычисления определителей в методе Крамера, для матриц общего вида, являющихся элементом СЛАУ, для решения этой задачи успешно может использоваться метод Гаусса. Прямой ход метода для системы 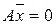позволяет вычислить

,

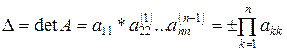так как последовательное исключение элементов величину определителя не изменяет. Здесь а_kk – элементы преобразованной матрицы А (прямой ход Гаусса). Знак зависит от четности или нечетности перестановок строк исходной матрицы при приведении ее к треугольному виду во избежание делении на «0» или необходимости поиска «max» ведущего элемента в текущем столбце на каждом этапе исключение неизвестных.

Для симметричных матриц

; .

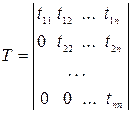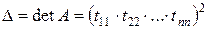1. По методу Гаусса. Всякая неособенная матрица, для которой 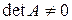, имеет обратную матрицу. Очевидно, что А * А ^–1 = Е. запишем это равенство в виде системы n уравнений с n неизвестными

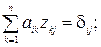
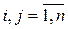; (37)

где а_ik – элементы матрицы А;

z_kj – элементы обратной матрицы (А ^–1);

d_ij – элементы единичной матрицы.

При этом d_ij =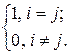

Для нахождения элементов одного столбца обратной матрицы необходимо решить соответствующую линейную систему (37) с матрицей А. Так для получения j -го столбца для А ^–1 (z _{1 j ,} z _{2 j},… z_nj) решается система:

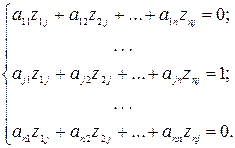(38)

Следовательно для обращения матрицы А нужно n раз решить систему (38) при j =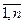. Поскольку матрица А системы не меняется, то исключение неизвестных осуществляется только один раз, а (n –1) раз при решении (38) делается только обратный ход с соответствующим изменением правой ее части.

2. Другой подход к определению обратной матрицы А^–1

,

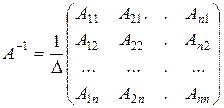где D – определитель матрицы, А_ij – алгебраические дополнения соответствующих элементов матрицы А.

Дата добавления: 2013-12-11