Волна. Плоская синусоидальная волна

Волновые процессы.

Резюме

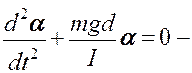· дифференциальное уравнение гармонических колебаний.

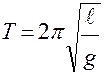· - математический маятник

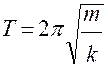· - пружинный маятник

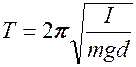· - физический маятник

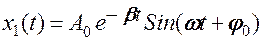· - затухающие колебания

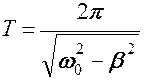· период затухающих колебаний.

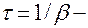· время релаксации (амплитуда колебаний уменьшается в e раз)

· δ = 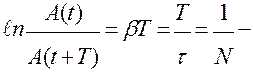логарифмический декремент затухания.

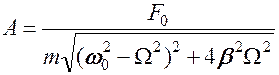· - амплитуда при резонансе

·

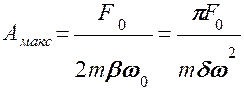
Л-9

Процесс распространения колебаний в сплошной среде - волна. При распространении волны частицы среды не движутся вместе с волной, а колеблются около положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от природы, является перенос энергии без переноса вещества.

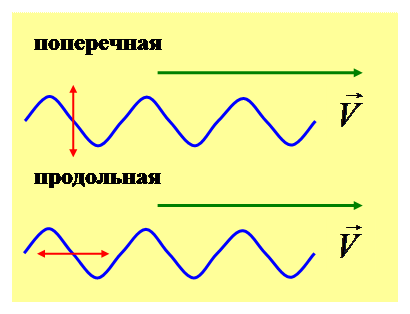
Продольные волны – частицы колеблются в направлении распространения волны,

Поперечные волны - частицы колеблются в направлениях, перпендикулярных направлению распространения волны.

Продольные волны – возникают в средах, в которых появляются упругие силы при деформации сжатия или растяжения, т.е. твёрдых, жидких и газообразных средах.

Поперечные волны – возникают в средах, в которых появляются упругие силы при деформации сдвига, т.е. фактически только в твёрдых телах; в жидкостях и газах возникают только продольные волны, а твердых телах – как продольные, так и поперечные.

O

x

x

λ

B

S

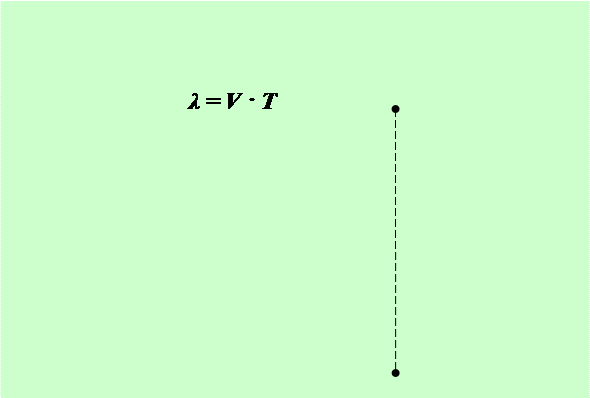
Длина волны λ – расстояние между ближайшими точками, колеблющимися в одинаковой фазе.

Волновой фронт – геометрическое место точек пространства, до которых доходят колебания к моменту времени t

Волновая поверхность - геометрическое место точек, в которых фаза колебаний имеет одно и то же значение. Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени – один.

Волна называется плоской – если её волновые поверхности являются плоскостями, параллельными друг другу.

Сферическая волна – волновые поверхности - сферы.

Бегущие волны – волны, переносящие в пространстве энергию. Перенос энергии волной количественно характеризуется вектором плоскости потока энергии – вектором Умова.

Пусть среда не поглощает, тогда колебания в какой-либо точке В отличаются от колебаний в начале координат О, происходящих по закону S = f(t), только тем, что они сдвинуты по времени на 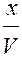, поэтому в плоской волне, распространяющейся вдоль положительного направления оси х, S являются функцией разности 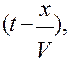поэтому уравнение такой плоской волны будет иметь вид

.

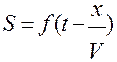Если волна распространяется в противоположном направлении, то

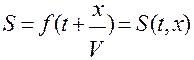
Для синусоидальной волны

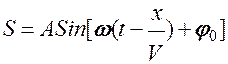но т.к. 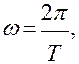то

или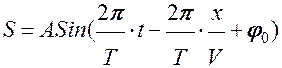

Величина в скобках - фаза Ф плоской волны.

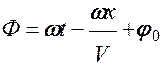
В этом случае

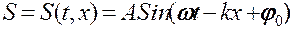
Это - уравнение бегущей волны.

Учитывая формулу Эйлера 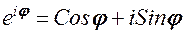уравнение волны можно записать в виде

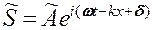
где .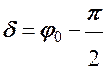

Фазовая скорость волны – скорость распространения в пространстве фазы волны (Ф = const).

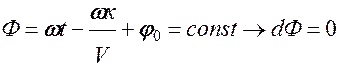
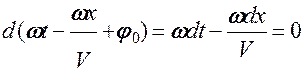
откуда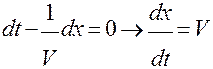

т.е. V – и есть фазовая скорость волны.

т.к. 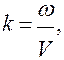то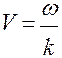

Дисперсия волн – зависимость их фазовой скорости в среде от частоты, а среда, в которой это наблюдается - диспергирующая среда.

Дата добавления: 2013-12-12