Лекция 1. КИНЕМАТИКА

Контрольные вопросы

Контрольные вопросы

Глава. 7. Атомные ядра

Контрольные вопросы

Глава 5. Квантовое строение кристаллов

Контрольные вопросы

Рис. 4.1. Распределение Бозе-Эйнштейна

И при T=0 населенным окажется только уровень с минимальной энергией. Можно показать, что существует такая отличная от нуля температура T0, при которой часть частиц останется на уровне с нулевой энергией, а остальные распределятся по более высоким уровням по закону (4.4) с m =0. Это явление, связанное с различным распределением по энергиям двух частей Бозе-газа называется Бозе-конденсацией. Следует иметь в виду, что вещество при этом остается идеальным газом и к обычной конденсации газа в жидкость стрем­ление части бозонов при понижении температуры собраться в одном квантовом со­стоя­нии с нулевой энергией не имеет отношения. Бозе–конденсация проявляется в таких макро­ско­пических физических явлениях, как сверхпроводимость, сверхтекучесть, индуци­рованное излучение света. Эти явления составляют основу прогресса в ряде направлений техники.

Глава 4. Элементы квантовой статистики

Контрольные вопросы

Рис. 3.6. Схема переходов в техуровневой лазерной системе

Рис. 3.4. Схема опыта Штерна-Герлаха

Рис.3.3. Спектр атома водорода

Глава 3. Строение атомов и молекул

Контрольные вопросы

Глава 2. Волновая механика

Контрольные вопросы

1. Какой опыт показывает наличие внутри атомов положительных ядер малого размера?

2. Поток фотонов с известной мощностью на единицу поверхности падает нормально на зеркальную поверхность. Как найти давление света на зеркало?

3. Чему равно изменение частоты фотона при его комптоновском рассеянии назад?

4. Как экспериментально можно измерить красную границу?

5. Какие практические применения имеет фотоэффект?

Волна де Бройля. Де Бройль выдвинул гипотезу о том, что волновые свойства присущи не только световым квантам, но и любым частицам вещества. Если принять, что соотношение между энергией и частотой 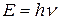и между импульсом и длиной волны 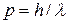, справедливое для фотонов, носит универсальный характер, то произвольной частице можно сопоставить некоторую волну

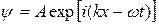, (2.1)

в которой 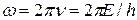, а 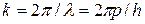. В результате подстановки этих соотношений в формулу (2.1) мы получаем выражение для 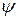-волны уже в терминах механических величин – энергии и импульса:

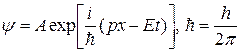. (2.2.)

Гипотеза де Бройля была непосредственно подтверждена в опыте Дэвиссона и Джермера (1927 г.), в котором при отражении электронных пучков от пространственной кристаллической решетки металлов была зафиксирована картина дифракции электронов. Проведенные расчеты дали значение длины волны для 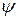-функции, находящееся в полном соответствии с гипотезой де Бройля.

Соотношение неопределенностей Гейзенберга. Для описания частиц при помощи волн требует уточнения вопрос об их локализации. Для того, чтобы разобраться в этом, рассмотрим прохождение 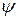-волны через узкое отверстие в непрозрачном экране. При прохождении частицы через щель ее координата фиксируется с точностью 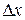. В результате дифракции частицы получают некоторый поперечный импульс 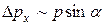, где a – характерный угол отклонения, который согласно теории дифракции волн на щели (уравнение 4.17) удовлетворяет соотношению 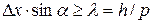. Таким образом, получаем соотношение 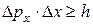. Оно накладывает ограничение на точность одновременного определения координаты и импульса частицы. Отметим, что в соотношении неопределенности Гейзенберга формулируется неопределенность координаты и проекции импульса на направление этой же координаты. Более строгое рассмотрение данного вопроса приводит к неравенству

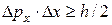, (2.3)

которое носит название соотношения (принципа) неопределенности Гейзенберга.

Принцип неопределенности относится и к одновременному измерению энергии E и времени t. Например, в качестве D E можно выбрать точность определения энергии фотона, а в качестве D t – промежуток времени, за который он был испущен. Принцип неопределенности для пары «энергия-время» утверждает, что

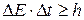. (2.4)

Здесь также ограничение накладывается только на произведение 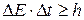, но не на степень точности каждой из величин в отдельности.

Статистический смысл волновой функции. Исходя из аналогии с оптикой, можно ожидать, что интенсивность потока частиц пропорциональна квадрату амплитуды волновой функции 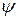. Поскольку в силу принципа неопределенности Гейзенберга говорить о точном местоположении частиц не имеет смысла, то подсчитать число частиц в данном объеме пространства dV можно лишь в среднем. Поэтому имеет смысл ввести понятие вероятности обнаружить частицу в данном объеме

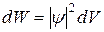. (2.3)

Тем самым волновая функция 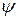описывает не физическое силовое поле, а является характеристикой, определяющей вероятности событий в мире микрочастиц. В этом заключается вероятностная интерпретация волновой функции.

Уравнение Шредингера. Из волновой теории нам известно, что всякому волновому движению соответствует некоторое дифференциальное уравнение. Для волны де Бройля такое уравнение можно получить исходя из классической связи между энергией и импульсом свободной частицы: 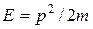. Нетрудно убедиться, используя выражения для 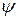функции (2.2), что

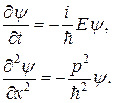(2.4)

Отсюда следует

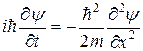. (2.5)

Если частица движется во внешнем потенциальном поле с потенциальной энергией U, то 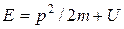и уравнение Шредингера для волновой функции принимает вид

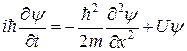. (2.6)

Для трехмерного движения это уравнение записывается в виде

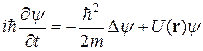, (2.7)

где 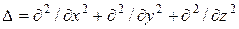– дифференциальный оператор Лапласа.

В случае если потенциальная функция не зависит от времени, то 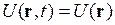и решение уравнения (2.7) имеет вид

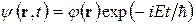(2.8)

Вероятность обнаружения частицы в некоторой области пространства для такого состояния не зависит от времени и определяется только пространственной частью волновой функции 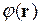. В самом деле.

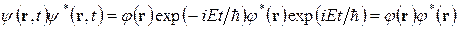(2.9)

Поэтому такие состояния называются стационарными. После подстановки функции (2.8) в уравнение (2.7) имеем

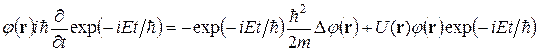. (2.10)

Учитывая, что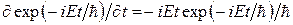, и сокращая множитель 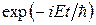в обеих частях равенства, получим стационарное уравнение Шредингера (в дальнейшем – уравнение Шредингера):

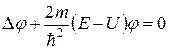. (2.11)

Уравнение Шредингера позволяет в принципе описать все явления микромира, кроме тех, которые связаны с теорией относительности. Оно, например, объясняет строение атомов, молекул, кристаллов и их спектры. Некоторые (например, магнитные) эффекты теории относительности могут быть учтены в рамках уравнения Шредингера, путем введения в него дополнительных слагаемых. При этом, конечно, последовательное решение дифференциального уравнения (2.6) (так же как и уравнения Ньютона) для произвольного вида взаимодействия U( r ) может быть весьма сложным. Мы решим уравнение Шредингера в двух простейших случаях, что позволит, не отвлекаясь на математические трудности, продемонстрировать физические особенности явлений микромира.

Частица в потенциальной яме. Рассмотрим волновое движение частицы, ограниченное двумя параллельными непроницаемыми отражающими стенками (рис. 2.1). Можно считать, что в промежутке между стенками движение свободное и потенциал равен нулю, а за стенками потенциал очень велик, и его можно принять равным бесконечности.

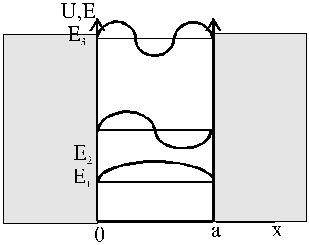
Рис.2.1. Частица в потенциальной яме шириной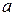

Между стенками волновая функция описывается уравнением

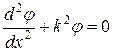, (2.12)

где 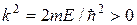. По виду это уравнение совпадает с уравнением гармонических колебаний при замене 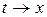с общим решением

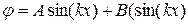, (2.13)

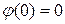где A и B пока произвольные константы. Вне потенциальной ямы с бесконечно высокими стенками частица находиться не может, т.е. вероятность ее нахождения там равна нулю. Поэтому на границах ямы . Из условия следует, что B = 0. Из условия 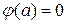следует, что

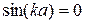. (2.14)

Отсюда

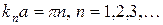. (2.15)

Следовательно

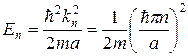. (2.16)

Числа натурального ряда 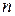называются квантовыми числами. Наименьшая возмож­ная энергия 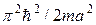отвечает n = 1, а соответствующая волновая функ­ция составляет половину синусоиды. Мы получили решение в виде стоячей волны. В общем случае пространственное ограничение движения микрочастиц приводит к возникновению различных стоячих волн. Условия их возникновения называются квантованием и характеризуются дискретными значениями параметров. В настоя­щее время потенциальные ямы реализованы в технологии тонких полупроводни­ковых пленок, а их электрические и оптические свойства тесно связаны с рассмот­ренной нами квантовой задачей.

Туннельный эффект. В классической механике нахождение частицы в области пространства, где потенциальная энергия больше полной, невозможно. Иначе обстоит дело в квантовой механике. Рассмотрим простой пример. Пусть зависимость потенциальной энергии от координаты имеет вид прямоугольной ступеньки, как показано на рис. 2.2.

Рис. 2.2. Прохождение волны через прямоугольный потенциальный барьер

Слева от точки 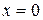потенциал 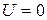, и частица движется свободно. В этой области она описывается волной де Бройля. В области 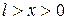потенциальная энергия 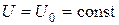. При 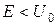классическое движение в этой области невозможно. В точке 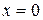налетающая на барьер классическая частица отразится. В квантовой механике движение частицы в области 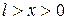описывается одномерным стационарным уравнением Шредингера (2.12), которое можно записать в виде

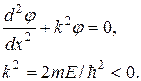(2.17)

Уравнение (2.17) имеет решение

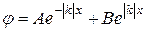, (2.18)

в чем можно убедиться прямой подстановкой. Пр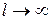и и 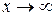решение должно затухать, поскольку частица не может выйти из-под барьера по физическому смыслу задачи. Поэтому 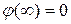и B = 0. Таким образом, волновая функция частицы в подбарьерной области экспоненциально затухает и

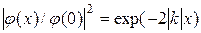. (2.19)

Формула (2.19) описывает вероятность проникновения частицы под потенциальный барьер на глубину 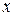. Если потенциальный барьер имеет произвольную форму, как показано на рис. 2.3, его можно представить в виде совокупности прямоугольных потенциальных барьеров.

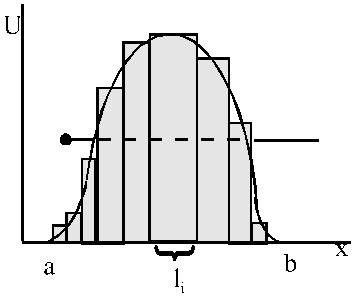
Рис.2.3. Плавный потенциальный барьер произвольной формы

Вероятность прохождения через каждый из прямоугольных потенциальных барьеров описывается формулой (2.17). Полную вероятность прохождения через барьер можно найти как произведение вероятностей прохождения через отдельные прямоугольные барьеры:

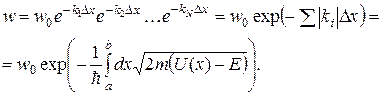(2.20)

Туннельный эффект позволяет объяснить целый ряд физических явлений, не находящих объяснения с точки зрения законов классической физики. Одно из таких явлений – автоэлектронная эмиссия, т.е. вырывание электронов из металла постоянным электрическим полем. Другое, о котором мы будем говорить позднее, – явление a -распада атомных ядер.

1. Как можно убедиться в волновой природе микрочастиц?

2. Какой характерный импульс имеет электрон, локализованный в атоме с размерами 10^{-8 см?}

3. Какой смысл имеет волновая функция?

4. Какая связь имеется между волновой функцией и волной де Бройля?

5. Запишите нестационарное и стационарное уравнение Шредингера.

6. Почему энергия свободного электрона может быть любой, а энергия электрона, запертого в ящике с отражающими стенками, оказывается дискретной?

Атом водорода. Объяснение строения и спектров атомов, молекул, ионов (для простых систем - во всех деталях) и их спектров стало одним из главных аргументов в пользу квантовой механики и окончательно убедило ученых в ее справедливости. Перейдем к описанию простейшего атома водорода, состоящего из атомного ядра и одного электрона, взаимодействие которых описывается законом Кулона

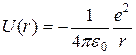. (3.1)

Уравнение Шредингера в этом случае имеет вид

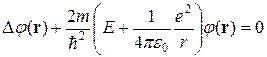. (3.2)

Данное уравнение является трехмерным, и его в общем случае довольно сложно. Однако высоковозбужденные состояния, вследствие принципа соответствия Бора, близки к классическим, и для них определение спектра энергий можно осуществить достаточно просто. При этом многие результаты, полученные для высоких состояний, верны и в общем случае.

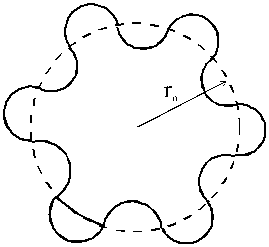
Рис. 3.1. Круговая орбита и стоячая волна в атоме водорода

Простейшей замкнутой траекторией классического движения в кулоновском поле является окружность (пунктир на рис. 3.1). Стационарность квантового со­стояния требует, чтобы вдоль траектории образовалась стоячая волна. Для этого необходимо, чтобы на траектории длиной 2 pr укладывалось целое число 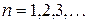волн де Бройля (сплошная линия на рис. 3.1), что при­водит к уравнению

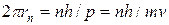. (3.3)

Здесь 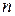называется главным квантовым числом. В уравнении (3.3) учтено, что высоковозбужденный электрон практически свободен и может описываться волной де Бройля. Кулоновская сила на круговой орбите является центростремительной. Учитывая, что центростремительное ускорение 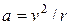, запишем второй закон Ньютона в виде

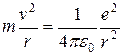. (3.4)

Рис. 3.2. Уровни энергии в атоме водорода

Отсюда следует,

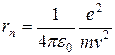. (3.5)

Поскольку в соответствии с уравнением (3.3)

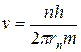, (3.6)

равенство (3.5) принимает вид

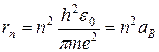. (3.7)

Здесь введено обозначение константы 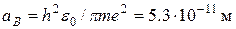, называемой боров­ским радиусом.

Квантование энергии в атоме водорода. Энергия состояния с квантовым числом n складывается из потенциальной энергии кулоновского взаимодействия электрона с ядром и кинетической энергии движения по круговой орбите:

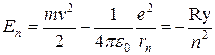. (3.8)

Здесь использованы соотношения (3.5) и (3.6) и введено обозначение для кон­станты Ридберга 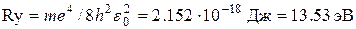. Таким образом, в области отрица­тельных энергий энергии располагаются более плотно с увеличением квантового числа (рис. 3.2). Состояние с минимальной энергией (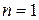) называется основным, а состояния с 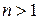- возбужденными. Можно показать, что положительные энергии распределены непрерывно (затемненная область на рис.3.2).

Разность энергий уровней с различными значениями главного квантового числа k, n определяет энергию фотона, излучающегося (при k>n) или поглощающегося (k<n) при переходе электрона из одного стационарного состояния в другое:

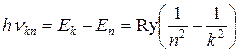. (3.9)

Вид спектра приведен на рис. 3.3. Экспериментально наблюдаемые энергии пере­ходов прекрасно согласуются с результатами расчетов по квантовой теории.

Состояние электрона в атоме водорода и спин электрона. Точное решение уравнения Шредингера (3.2) свидетельствует о том, что кроме ранее введенного квантового числа n, называемого главным, состояние электрона в атоме водорода характеризуется также орбитальным l и магнитным m квантовыми числами. Орбитальное (иногда азимутальное) число принимает n значений l= 0,1,2,3… n -1. Магнитное квантовое число принимает 2 l+ 1 значение m= - l,- l +1,…. l -1, l. Магнитное квантовое число определяет проекцию механического момента 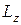на направление :

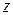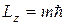. (3.10)

Орбитальное квантовое число определяет величину полного момента количества движения при орбитальном движении

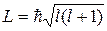. (3.11)

Электрон по современным представлениям является точечным объектом. Несмотря на это, учет релятивистских эффектов приводит еще одному квантовому числу m_S - спину, принимающего два значения 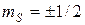, харак­теризую­щего собственный момент количества движения.

Проекция спинового момента на ось 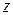равна

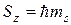, (3.12)

а полный спиновый момент

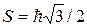. (3.13)

Наличие собственного меха­нического момента – спина у заряженной частицы означает, что у электрона должен быть и собственный магнитный момент. Это наглядно проявилось в опыте Штерна и Герлаха (рис. 3.4). Если поток атомов водорода пропустить через диафрагму Д, то в результате получится узкий атомный пучок. Далее он проходит через неоднородное магнитное поле, создаваемое магнитом с полюсами S и N. В результате на экране Э образуются два четко разделенных пятна от атомов. Это означает, что магнитный момент атома водорода может иметь два противоположных значения. Полный момента атома находится путем векторного сложения орбитального и спинового моментов количества движения. Поскольку в основном состоянии атома водорода орбитальный момент электрона равен нулю, то наличие ненулевого момента у всего атома может означать только существование дополнительного момента у электрона – спина.

Принцип Паули. Состояние электрона в атоме водорода полностью описывается четырьмя квантовыми числами: n,l,m,m_S. Состояния, отличающиеся хотя бы одним квантовым числом, различны, хотя их энергии в атоме водорода зависят только от главного квантового числа и могут совпадать. Простота описания атома водорода в квантовой механике связана с тем, что в этой задаче имеется единственный электрон, движущийся в центральном поле атомного ядра, описываемом законом Кулона. В многоэлектронном атоме важным становится учет взаимодействия электронов между собой. Однако если электронов достаточно много, то атом остается близким к сферически симметричной форме, а среднее поле электронов близким к центральному потенциалу, в котором достаточно сильно проявляется поле атомного ядра. В силу этого ряд свойств атома водорода сохраняется, пусть в несколько модифицированном виде, и в сложных атомах.

В то же время в многоэлектронных системах проявляется и принципиально новое свойство электронов. Оказывается, что в одном стационарном квантовом состоянии может находиться только один электрон. Состояния любых двух электронов должны различаться хотя бы одним квантовым числом, например, направлением спина. Это составляет содержание принципа запрета Паули, которому кроме электронов подчиняются и другие частицы, имеющие полуцелый спин (в единицах 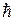). Все частицы с полуцелым спином называются фермионами. Принцип Паули позволяет объяснить последовательность заполнения атомных оболочек и подоболочек в сложных атомах с ростом номера элемента и дает теоретическое объяснение периодической системы элементов Менделеева. Этот вопрос подробно рассматривается в курсе химии, и мы на нем подробно не останавливаемся.

Строение и спектры молекул. При сближении атомов их внешние валентные электроны вступают во взаимодействие и могут обеспечивать устойчивую связь групп атомов. Такие связи называются химическими, а устойчивые группы атомов – молекулами. Типы химических связей, условия возникновения молекул и их взаимные превращения изучаются в химии. Особенности строения молекул обеспечивают многообразие их физических и химических свойств.

В молекуле по сравнению с атомом появляются новые степени свободы – колебательная и вращательная. Поскольку молекулы состоят из нескольких атомов, то в них имеется несколько тяжелых центров – атомных ядер. Атомные ядра в молекуле связаны квазиупругими силами и могут совершать колебательные движения друг относительно друга. Энергии при колебательном движении квантовой частицы принимают дискретный ряд значений

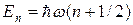, (3.14)

где n = 0, 1, 2…, w – частота колебательного кванта. Минимальная энергия квантового осциллятора отлична от нуля, что соответствует принципу неопределенности. Молекула в целом представляет собой тело, способное совершать вращательное движение. В классической механике с вращательным движением связана энергия

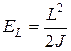. (3.15)

Здесь L – момент количества движения молекулы, J – ее момент инерции. В квантовой механике

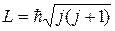, (3.16)

где j – целое или полуцелое квантовое число, которое образуется в результате

сложения орбитальных и спиновых моментов электронов и ядер. Соответственно вращательную энергию молекулы можно записать в виде

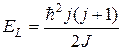. (3.17)

Кроме того, в молекулах имеется большое число электронов, которые могут возбуждаться без существенного изменения колебательного или вращательного движения молекул. Если обозначить их энергию 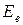, то энергия покоящейся молекулы без учета внутренней энергии атомных ядер может быть записана в виде

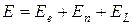. (3.18)

Отмеченные особенности энергетического строения молекул приводят к образованию характерных колебательных и вращательных полос в их спектрах. Этим они резко отличаются от атомных спектров, имеющих вид отдельно расположенных линий. Вид молекулярного спектра приведен на рис. 3.5.

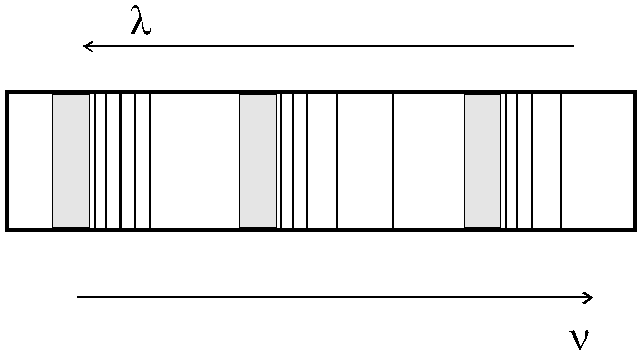
Рис. 3.5. Полосатый спектр излучения молекулы

Излучение и поглощение света атомами и молекулами. Мы уже отмечали ряд важных свойств и особенностей взаимодействия электромагнитного излучения с веществом. Однако научная и практическая важность этого круга явлений столь велика, что необходимо остановиться еще на ряде важных оптических явлений, законов и их приложениях.

Поскольку спектры излучения атомов и молекул являются индивидуальными для данного вида вещества, то на основе их классификации создан спектральный анализ, который позволяет определить состав вещества и долю в нем тех или иных атомов и молекул. Спектральный анализ, в частности, широко применяется в металлургии при контроле выплавки стали.

Кроме поглощения света веществом возможны и другие виды взаимодействия фотонов с атомами и молекулами. При упругом рассеянии фотонов молекулами частота света n не меняется, а меняется только направление движения фотона. При неупругом рассеянии энергия рассеянного фотона отличается от энергии падающего фотона на разность энергий молекулы или атома в начальном и конечном состояниях D E. Соответственно изменяется частота:

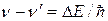. (3.19)

Такое рассеяние света называется комбинационным. Чаще всего частота рассеянного фотона 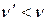, поскольку большая часть молекул при нормальных условиях находится в основном состоянии и молекулы при рассеянии на них фотонов могут только приобретать энергию.

По этой же причине распространяющийся в веществе свет обычно испытывает поглощение. Если интенсивность света на некоторой глубине x в веществе составляет величину 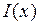, то доля поглощенного света пропорциональна толщине тонкого дополнительного слоя dx:

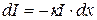, (3.20)

где величина k носит название коэффициента поглощения вещества. Проинтегрировав уравнение (3.20), получаем закон Бугера:

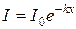. (3.21)

Здесь 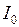– интенсивность света при x = 0. Коэффициента поглощения вещества зависит от длины волны l. Для фиксированной величины l он определяется числом частиц, находящихся в состояниях, между которыми происходит переход:

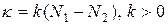. (3.22)

В обычных условиях термодинамического равновесия распределение электронов по энергиям подчиняется распределению Больцмана, и количество электронов N ₂ в верхнем состоянии меньше числа электронов N ₁ в более низком энергетическом состоянии. В этих условиях k > 0 и формула (3.20) характеризует ослабление света.

Принцип действия лазера. Если за счет внешних, неравновесных с данной средой источников возбуждения (электронного удара, электромагнитных волн, химических реакций и других), обеспечить инверсную населенность, при которой 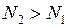, то k < 0 и в среде будет происходить усиление света. Этот механизм является физической основой действия оптических квантовых генераторов – лазеров.

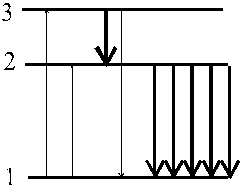
Инверсная населенность может быть получена в системе, обладающей, например, тремя дискретными энергетическими уровнями, время жизни среднего из которых значительно (в реальных устройствах в 10⁴ – 10⁵ раз) больше, чем у лежащих выше (рис. 3.6). Такой уровень называется метастабильным. При воздействии внешних источников электроны переходят из состояния 1 в состояния 2 и 3 с большей энергией, так что больше всего возбуждается состояния 3. Эти процессы отражены на рис 3.6 тонкими вертикальными стрелками. Переход электронов с уровней 2 и 3 в состояния 1 с излучением фотона может происходить как спонтанно, так и вынужденно. При этом наиболее вероятным переходом из состояния 3 оказывается безрадиационный переход в ближайшее состояние 2. В твердых телах такой переход осуществляется за счет передачи части энергии кристаллической решетке. Вследствие метастабильности состояния 2 на нем происходит накопление электронов. В результате этого населенность уровня 2 оказывается большей, чем основного состояния 1, т.е. выполняется условие инверсности 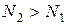. Индуцированный переход 2→1, под действием квантов, частота которых удовлетворяет условию

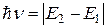, (3.23)

имеет высокую вероятность по сравнению с соответствующим спонтанным переходом. Первичный индуцирующий квант может быть как внешним, так и полученным в результате спонтанного перехода из метастабильного состояния в основное состояние. При этом вторичный испущенный фотон тождествен первичному фотону и также может вызвать вынужденный переход 2→ 1. Вследствие этого число фотонов, частота которых удовлетворяет условию (3.23), растет лавинообразно и стимулированное излучение имеет высокую мощность.

Для получения излучения с большой длиной когерентности и острой направленностью луча используется оптический резонатор – система двух параллельных зеркал, одно из которых полупрозрачное, между которыми находится инверсная среда (рис. 3.7).

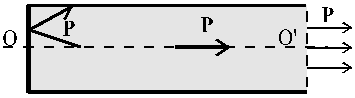
Рис. 3.7. Схема работы лазера

Если первичный фотон распространяется вдоль оси резонатора ОО΄, фотонная лавина растет до тех пор, пока сохраняется условие инверсной населенности. Если угол между импульсом фотонов и осью ОО´ не равен нулю, развитие фотонной лавины обрывается при поглощении излучения боковыми стенками резонатора. Расходимость луча лазера определяется в основном дифракцией на выходном отверстии. Высокая мощность и когерентность лазерного излучения нашли многочисленные практические применения в связи, обработке материалов, метрологии и дистанционном зондировании природных объектов.

1. Что такое азимутальное квантовое число и магнитное квантовое число?

2. Как можно экспериментально убедиться в существовании спина электрона?

3. Сформулируйте принцип Паули.

4. Какие характерные виды возбуждений есть у молекулы?

5. В чем заключается комбинационное рассеяние света?

6. Почему одно и то же вещество в одних условиях может поглощать свет, а в других – усиливать его?

Квантовая и статистическая вероятности. Понятие вероятности применяется и в статистической физике и в квантовой меха­нике, однако смысл вероятности в этих разделах физики существенно отлича­ется. В квантовой механике, если мы рассмотрим волну де Бройля, падающую на экран, то она описы­вает движение электрона с определенным импульсом, но с неопределенной координатой. Такой электрон с равной вероятностью может попасть в любую точку экрана. До попадания на экран даже у отдельного электрона нет определенной координаты.

В классической статистике, наоборот, мы имеем большое число одинаковых частиц – атомов или молекул, каждая из которых в данный момент времени находится в строго определенном месте и двигается с определенной скоростью. Здесь вероятность возникает в результате того, что мы рассматриваем макроскопические свойства больших систем, в которых детали движения отдельных атомов и молекул несущественны. Тем самым можно ввести, например, распределение частиц по скоростям и говорить о доли частиц со скоростями в указанном интервале. Если мы имеем дело с ансамблем микрочастиц, то при его описании необходимо учитывать статистические свойства, связанные и с их квантовым поведением, и с тем обстоятельством, что имеется большое число одинаковых частиц.

Проще формулировать и решать задачи статистической физики в терминах фазового пространства, с частным случаем которого – фазовой плос­костью мы уже встречались при изучении нелинейных колебаний и автоколебаний. В общем случае фазовым пространством системы с s степенями свободы называется пространство размерностью 2 s, на координатных осях которого отложены значения s координат q_i и s импульсов p_i системы. Произведение координат фазового пространства называется фазовым объемом. Каждому состоянию системы со­ответствует оп­ределенная точка фазового пространства (фазовая точка), а изме­нение состояния системы во времени описывается фазовой траекторией. В клас­сической физике положение фазовой точки можно указать сколь угодно точно.

В квантовой механике принцип неопределенности накла­дывает ог­раничение на точность определения фазовых координат. О фазовой точке можно лишь сказать, что она занимает в элементарной ячейке фазового пространства объем

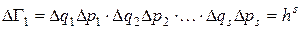. (4.1)

Таким образом, число квантовых состояний g, содержащихся в некотором фазовом объеме DG, есть

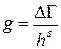. (4.2)

Кроме принципа неопределенности в квантовой статистике важен принцип нераз­личимости тождественных частиц, согласно которому системы, отличающиеся только перестановкой одинаковых частиц, физически эквивалентны.

Квантовые идеальные газы. Изучение статистических свойств естественно начать с идеальных газов - простейших систем невзаимодействующих частиц. Каждая из N частиц идеального газа имеет 3 степени свободы. Поэтому размерность фазового пространства такого газа равна 6 N. При этом фазовое пространство идеального газа разбивается на независимые подпространства – координатное и импульсное, размерностью 3 N каждое. Связь энергии с импульсом E=p² /2 m позволяет преобразовать импульсное подпространство в энергетическое. Эта операция будет проделана позже при изучении электронного газа в металлах. Среднее число частиц, находящихся в одном состоянии с энергией E_i равно

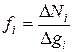(4.3)

и называется заселенностью энергетического уровня. Здесь 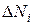– число частиц с энергией в интервале от E_i до 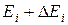, 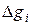– число квантовых состояний в этом интервале энергий.

В классической статистике большинство свойств идеального газа не зависит от свойств составляющих его частиц. В квантовой механике частицы делятся на два класса – фермионы (или более полно – частицы, подчиняющиеся статистике Ферми-Дирака) и бозоны (частицы, подчиняющиеся статистике Бозе-Эйнштейна), статистические свойства которых принципиально отличаются.

Спин фермионов в единицах 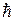полуцелый: 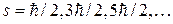. Следствием принципа неразличимости тождественных частиц для фермионов является принцип Паули, согласно которому заселенность состояния может принимать только два значения – ноль и единицу. Фермионом является, например, электрон. Электроны отрицательно заряжены, поэтому они могут образовать идеальный газ либо при малых плотностях и высоких температурах, либо когда их заряд скомпенсирован распределенным в пространстве положительным зарядом.

Спин бозонов в единицах 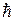нулевой или целый: 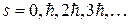. Бозоны не подчиня­ются принципу Паули, и в одном состоянии может находиться любое их число. В частности, бозонами являются фотоны. Фотоны практически не взаимодействуют друг с другом и обра­зуют идеальный газ при любых условиях. Кроме того бозонами являются некоторые атомные ядра (важный пример - ядра ⁴₂ He или a -частицы) и другие частицы.

Даже невзаимодействующие фермионы не явля­ются независимыми. Так, заселение уже занятого состояния фермионом вследствие прин­ципа Паули невозможно, и населенность уровня не может быть больше единицы. В противоположность этому, заселенность состояния бозонами может быть произвольной. Если в каждом состоянии в среднем находится гораздо меньше одной частицы, это различие между разными статистиками не сказывается на поведении системы. Если же большинство состояний оказывается занятым хотя бы одной частицей, это различие приводит к качественным отличиям в поведении систем невзаимо­действующих фермионов и бозонов. В целом говорят о двух разных типах статистик Бозе-статистке и Ферми-статистике.

Распределение Бозе-Эйнштейна. Для идеального газа бозонов зависимость средних чисел заполнения состояний с энергией E_i от абсолютной температуры T имеет вид

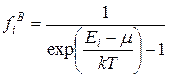, (4.4)

где k – постоянная Больцмана, m – химический потенциал системы. Химическим потенциалом системы называется энергия, необходимая для удаления частицы из системы при постоянном давлении и температуре. Физический смысл имеют только положительные числа заполнения. Поэтому для бозонов 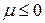, и, таким образом, показатель экспоненты при любой энергии неотрицателен. В пределе 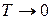он растет 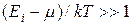, и слагаемым –1 в знаменателе формулы (4.4) можно пренебречь. В этом пределе распределение Бозе-Эйнштейна, как и должно быть в соответствии с принципом соответствия Бора, переходит в распределение Больцмана:

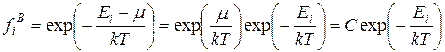. (4.5)

Здесь нормировочная константа 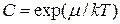, а следовательно и химический потенциал m, может быть найден из условия равенства суммы чисел заполнения числу частиц газа N

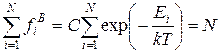. (4.6)

Из уравнения (4.5) следует, что отношение населенностей определяется раз­ностью энергий уровней

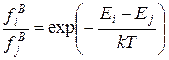, (4.7)

График зависимости чисел заполнения идеального Бозе-газа от энергии при разных температурах приведен на рис 4.1. Максимум в точке 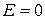отражает явление Бозе- конденсации.

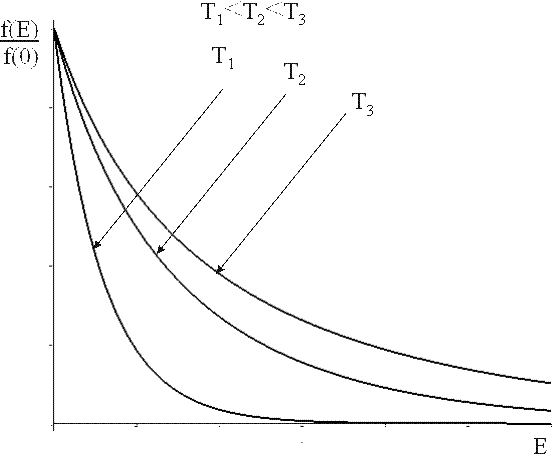
Можно показать, что для фотонов m = 0. Энергия фотона определяется его частотой:

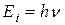. (4.8)

Распределение Бозе-Эйнштейна (4.4) значительно упрощается и принимает вид распределения Планка.

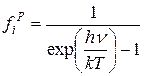. (4.9)

Фононы. Для газов, жидкостей и аморфных сред мы рассматривали распространение волн в приближении непрерывной среды. При исследовании распространение волн в кристаллических телах, при длинах волн, сравнимых с периодом кристаллической решетки, не учитывать периодическую структуру вещества уже нельзя.

Как и в любой системе, распространение волны в кристаллах происходит за счет упругого взаимодействия его соседних элементов. В кристаллах упругими силами связаны между собой атомы или ионы. Они могут совершать колебания двух видов. В одном случае соседние атомы, расположенные на отрезке, много меньшем длины волны, колеблются в противоположной фазе. Если решетка состоит из чередующихся атомов двух типов, то происходит колебание одной подрешетки относительно другой. Эти колебания называют оптическими.

Другой вид колебания вызывается однонаправленным смещением атомов в кристаллической решетке, при котором расстояние между соседними атомами меняется меньше, чем их общее смещение (синфазная мода). При таких колебаниях кристал­лическая решетка может приближенно рассматриваться как сплошная однородная среда. С такими колебаниями связаны звуковые волны.

Если энергия произвольного внутреннего движения кристалла невелика, то это движение всегда может быть разложено на плоские монохроматические волны, распространяющиеся независимо друг от друга. Согласно гипотезе де Бройля с монохроматической волной связана частица (квант), энергия которой связана с частотой волны соотношением .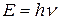

Квант звуковой волны называется фононом. Свойства фононов близки к свойствам фотонов. Так, энергия фононов связана с их частотой так же, как и у фотонов. Фононы, как и фотоны, подчиняются статистике Бозе. На языке фононов разогрев кристаллической решетки означает повышение температуры фононного газа. При малых амплитудах колебаний в идеальных кристаллах оптические и звуковые колебания можно считать независимыми. Не взаимодействуют между собой в этом случае и различные фононы, вследствие чего фононный газ можно считать идеальным. Тогда его функция распределения описывается формулой, подобной формуле Планка для спектральной плотности фотонов, излучаемых абсолютно черным телом (4.9). В реальных кристаллах условия идеальности фононного газа хорошо выполняются в обычных условиях.

Фононы обладают характерными свойствами частиц, однако не являются фундаментальными частицами, а возникают как возбуждение в конденсированной среде и не существует вне вещества. Поэтому фононы называют квазичастицами.

Распределение Ферми-Дирака. Если все бозе-частицы при 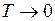переходят в одно основное состояние, то для фермионов, – частиц с полуцелым спином, нахождение двух частиц в одном квантовом состоянии запрещено принципом Паули. Соответственно распределение фермионов по энергиям имеет более протяженный характер. Оно записывается в виде

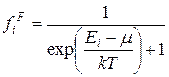(4.10)

и называется распределением Ферми-Дирака. Химический потенциал в распределении (4.10) может быть как отрицательным, так и положительным.

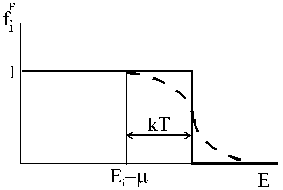
Рис. 4.2. Распределение Ферми-Дирака

Поскольку при любых значениях параметров 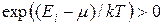, то в полном соответствии с принципом Паули средние числа заполнения ограничены сверху единицей: 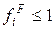. При больших энергиях возбуждения оно так же, как и распределение Бозе (4.4), переходит в классическое распределение Больцмана.

При близкой к абсолютному нулю температуре значение функции 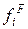скачком меняется при изменении энергии в точке 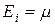. Если 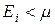, то 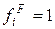, а при 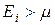числа заполнения равны нулю: 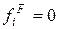. Тем самым, распределение приобретает вид ступеньки (сплошная линия на рис. 4.2). При 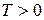переход от заполненных состояний к состояниям с нулевыми числами заполнения происходит в окрестности химического потенциала шириной 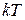, и ступенька размывается (пунктир на рис. 4.2).

Электронный газ в металлах. Электроны в металле ведут подобно идеальному ферми-газу, поскольку их взаимное отталкивание почти полностью компенсируется полем положительно заряженных ионов кристаллической решетки. При малых температурах все состояния с энергией 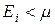оказываются заполненными электронами. Поэтому количество состояний, энергия которых меньше химического потенциала, совпадает с количеством электронов. Величина m носит в этом случае название энергии Ферми и обозначается .

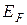Вычислим плотность электронов в металле при нулевой температуре. Для этого подсчитаем число свободных состояний, считая электроны идеальным газом. Фазовый объем для одной частицы идеаль­ного газа есть произведение геомет­риче­ского объема V на объем в пространстве импульсов 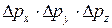. Поскольку энер­гия не зависит от направле­ния импульса, элемен­тарный фазовый объем, соот­ветствую­щий интервалу энергий 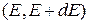, получается суммированием эле­ментар­ных объемов 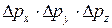, находя­щихся в соответствующем интервале модуля импульсов 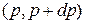. Результатом суммирования является объем шаро­вого слоя 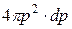(рис. 4.3).

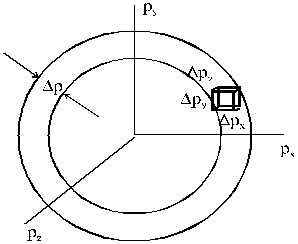
Рис. 4.3. Объем шарового слоя в пространстве импульсов

Учитывая два возможных значения спинового числа электрона, в соответствии с формулой (4.2) получим для числа допустимых состояний в объеме V выражение 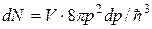. Для плотности состояний одного электрона 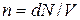, с учетом связи между импульсом и энергией 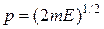, имеем

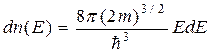. (4.11)

Общее число электронов проводимости в единице объема металла можно найти, проинтегрировав выражение (4.11) по энергии от 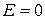до :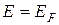

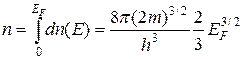. (4.12)

Если взять типичную концентрацию электронов в металле n = 6·10²⁸ м^-3, то

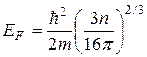= 9·10^-19 Дж = 5.4 эВ. (4.13)

1. Чем отличаются вероятности в статистической физике от вероятностей в квантовой механике?

2. Почему в определенном фазовом объеме имеется конечное число квантовых состояний?

3. Постройте график распределения Бозе-Эйнштейна.

4. Как связаны между собой распределение Бозе-Эйнштейна и формула Планка?

5. Чем отличается фотон от фонона?

6. Как выглядит распределение Ферми-Дирака при ?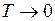

7. Почему электрон проводимости в металле можно рассматривать как идеальный ферми-газ?

Зонное строение кристаллов. При переходе в конденсированное состояние атомы сближаются так, что электронные облака их валентных электронов перекрываются. При этом происходит расщепление каждого энергетического уровня на N подуровней, где N – число атомов в системе. В периодической кристаллической структуре группа близко расположенных уровней образует энергетическую полосу или энергетическую зону. Энергетические уровни в зоне, образованной валентными электронами, отстоят друг от друга приблизительно на 10^-22 эВ. Разрешенные энергетические зоны разделены зонами запрещенных значений энергии электронов. Внутренние электроны атомов остаются практически в тех же состояниях, что и в изолированных атомах. Эти электроны сильно связаны с ядром и не принимают участия в процессах электропроводности и теплопроводности. В дальнейшем они не будут приниматься во внимание.

За счет расщепления уровней валентных электронов образуется валентная зона. Ширины зон, образованных возбужденными состояниями атомов, превышают расстояние между ними, вследствие чего образуется разрешенная зона, называемая зоной проводимости. Строение энергетических уровней кристаллов изображено на рис. 5.1.

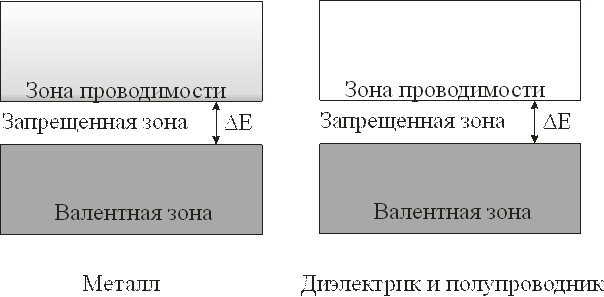
Рис. 5.1. Строение энергетических зон. Плотность заливки зон пропорциональна заселенности энергетических уровней.

Электроны в твердых телах могут переходить из одной разрешенной зоны в другую, для чего необходимо затратить энергию, равную ширине запрещенной зоны. Для внутризонных переходов достаточно весьма малой энергии 10^-4 эВ. Такой энергией обладают электроны при температуре около 1 К.

Зонное строение металлов, диэлектриков и полупроводников. Разрешенные энергетические зоны в твердом теле могут быть различным образом заполнены электронами. В предельных случаях они могут быть целиком заполнены электронами или совершенно свободны. Электрические свойства твердых тел определяются различным заполнением разрешенных энергетических зон и шириной запрещенных зон. Эти два фактора определяют принадлежность данного твердого тела к проводникам электрического тока, полупроводникам или диэлектрикам. Электрический ток есть движение электронов, при котором они переходят из одного состояния в другое. Вследствие принципа Паули переходы электронов в заполненной зоне происходить не могут и, следовательно, они не могут участвовать в создании тока.

В металлах валентные электроны полностью заполняют валентную зону и частично зону проводимости. При этом в некоторых металлах разрешенные зоны перекрываются. Под действием внешнего электрического поля валентные электроны увеличивают свою энергию и переходят на более высокие свободные энергетические уровни в зоне проводимости. Расстояние между соседними уровнями в зоне проводимости мало. Энергии электрического поля оказывается достаточно для придания электрону необходимой для внутризонного перехода энергии. Под действием поля электроны приходят в упорядоченное движение, и по металлу идет ток.

В диэлектриках и полупроводниках валентная зона заполнена, а зона проводимости при T= 0 совершенно пуста. Для создания тока необходимо освободить уровни валентной зоны или частично заполнить уровни зоны проводимости. Сделать это можно несколькими способами.

1. Во-первых, при больших напряжениях электрического поля проводимость возникает в форме пробоя, когда электроны в зоне проводимости высвобождаются электронным ударом и их число нарастает лавинообразно. Пробой чаще всего приводит к повреждению исходной структуры твердого тела.

2. Во-вторых, электрон может получить от кристаллической решетки тепловую энергию порядка kT, достаточную для перехода в зону проводимости.

3. Этот переход может быть осуществлен и за счет энергии светового кванта hn.

В этих случаях кристалл приобретает способность проводить ток. При этом, ширина запрещенной зоны полупроводника меньше энергии связи его частиц и возбуждение электронов в зону проводимости не сопровождается разрушением структуры кристалла. В диэлектриках энергия необходимая для межзонного перехода превышает энергия связи, вследствие чего возбуждение электрона сопровождается разрушением структуры кристалла.

Собственная и примесная проводимость полупроводников. Различие между диэлектриками и полупроводниками состоит в ширине запрещенной зоны DE. Если для диэлектриков она равна нескольким эВ, то для полупроводников DE £ 1эВ. Типичными полупроводниками являются такие химические элементы, как германий, кремний и теллур в кристаллической форме. Электропроводность химически чистых полупроводников называется собственной проводимостью. Удельное сопротивление 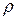полупроводников и диэлектриков определяется числом электронов в зоне проводимости и очень сильно убывает с ростом температуры. Для полупроводников оно изменяется в широком интервале от 10^-5 до 10⁸ Ом·м. Расчет, основанный на использовании распределения Ферми-Дирака, дает зависимость удельного сопротивления чистых полупроводников от температуры в виде

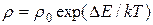. (5.1)

Электронная проводимость (проводимость n-типа) возникает при перебросе электронов из валентной зоны в зону проводимости. Для этого нужно затратить энергию не меньше, чем ширина D E запрещенной зоны, которая называется энергией активизации собственной проводимости. С ростом температуры полупроводника растет число электронов, которые вследствие теплового возбуждения переходят из валентной зоны в зону проводимости и участвуют в электропроводности.

Перевод электрона из валентной зоны в зону проводимости означает, что в оставленном им месте возникает избыток положительного заряда – положительная дырка. Положительная дырка ведет себя как положительный заряд, равный по величине заряду электрона. На освобожденное электроном место (дырку) может переместиться другой электрон, а это равносильно движению дырки. Во внешнем электрическом поле электроны двигаются противоположно направлению напряженности электрического поля, а дырки – по его направлению. Электропроводность полупроводника, обусловленная перемещением дырок, называется дырочной проводимостью или проводимостью p-типа.

В химически чистом полупроводнике с идеальной решеткой число носителей обоих типов совпадает. Введение в полупроводник примеси нарушают периодическое электрическое поле в кристалле. Энергетические уровни примесных атомов лежат в запрещенной зоне. В зависимости от расположения примесных уровней возможно увеличение вклада проводимости p или n типа. Даже малые (~0.001%) примеси сильно повышают электропроводность полупроводников. Примесные центры могут возникать также в результате различных дефектов и искажений в кристаллической решетке (пустые узлы, сдвиги при деформациях кристалла и др.). На фоне четырехвалентных атомов полупроводников обычно используются пяти- и трехвалентные атомы примеси, образуя донорные и акцепторные уровни соответственно. С донорных уровней, расположенных вблизи дна зоны проводимости, электроны легко переходят в зону проводимости, образуя электронную проводимость n -типа. Акцепторные уровни, расположенные вблизи вершины валентной зоны, легко захватывают электроны из валентной зоны, образуя в ней дырки и обеспечивая дырочную проводимость p -типа.

Квантовый механизм электропроводности металлов. В противоположность диэлектрикам и полупроводникам концентрация электронов в зоне проводимости металлов практически не зависит от температуры. Проводимость металлов определяется длиной свободного пробега электронов, уменьшающейся с ростом температуры. Это связано с увеличением амплитуды колебаний решетки и усилением вследствие этого рассеяния электронов на них. При коллективном описании внутреннего движения в кристалле этот эффект соответствует увеличению энергии фононов и усилении электрон-фононного взаимодействия. Вследствие этого сопротивление металлов с увеличением температуры увеличивается. Упорядоченное движение электронов в металле, – электрический ток, рассматривается в квантовой теории как процесс распространения электронных дебройлевских волн, которые рассеиваются на ангармонических тепловых колебаниях узлов решетки металла. При распространении волн любой природы в среде с неоднородностями, расположенными на расстоянии порядка длины волны l друг от друга, происходит их эффективное рассеяние. Если расстояние между центрами рассеяния много меньше l, то среда становится однородной для волны и рассеяния не происходит. Идеальная кристаллическая решетка, в которой отсутствуют нарушения периодичности, ведет себя как однородная среда для электронных волн (так называемых волн Блоха). Уравнение волн Блоха имеет вид аналогичный волнам де Бройля

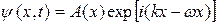, (5.2)

амплитуда которых не является постоянной, а представляет собой периодическую функцию координаты с периодом, равным постоянной кристаллической решетки b:

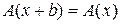. (5.3)

Аналогично волнам в свободном пространстве, в строго периодическом потенциале идеальной кристаллической решетки волны Блоха не затухают. Затухание и рассеяние электронных волн происходит при появлении искажений периодичности, которые являются центрами рассеяния. Такими центрами могут служить тепловые флуктуации плотности в решетке кристалла, а также примеси и дефекты. Рассеяние электронных волн на неоднородностях приводит к электрическому сопротивлению. Удельное сопротивление r металла состоит из двух частей:

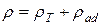. (5.4)

Здесь 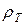– удельное сопротивле­ние, которое обусловлено рас­с

Дата добавления: 2013-12-12