Наращение процентов и инфляция

Эквивалентность процентных ставок

Иногда для принятия какого-либо финансового решения необходимо определить эквивалентность ставок процентов.

Эквивалентные процентные ставки – это такие ставки разного рода, применение которых при различных начальных условиях даст одинаковые финансовые результаты.

Для нахождения эквивалентных ставок процентов применяется уравнение эквивалентности, которое составляется по следующему принципу:

берется величина, которую можно рассчитать при использовании различных процентных ставок (обычно S). На основе равенства двух выражений для данной величины и составляется уравнение эквивалентности, из которого путем соответствующих преобразований выводим соотношение, выражающее зависимость между ставками процентов разного вида.

В предыдущих примерах все денежные величины измерялись по номиналу, т.е. не учитывалась изменившаяся во времени реальная покупательная способность денег. Однако сегодня при финансовых вычислениях делать поправку на инфляцию желательно, а иногда необходимо.

Учет инфляции важен как при расчете наращенной суммы, так и при определении действительной ставки процента.

Падение покупательной способности денег за период n характеризуется с помощью индекса:

,

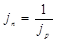где 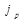- индекс цен

Реальная наращенная сумма денег с учетом их покупательной способности:

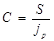
где C – реальная сумма денег

S – наращенная сумма денег за n лет

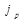- индекс цен

Допустим, что ожидаемый среднегодовой темп инфляции (прирост цен) = h. Тогда годовой индекс цен составит (1 + h). За n лет при сохранении предполагаемого темпа индекс цен будет равен .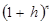

А величина, показывающая во сколько раз в среднем выросли цены, наз. индексом инфляции.

Наращенная сумма к концу этого срока с учетом ее обесценивания в связи с инфляцией составит:

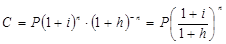
где 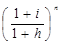- множитель наращения, учитывающий среднегодовые темпы инфляции

Если темп прироста инфляции = ставке начисляемых процентов, то покупательная способность наращенной суммы будет равна покупательной способности первоначальной суммы, т.е. C = P.

Выделяют положительную процентную ставку, когда h < i, т.е. это такая процентная ставка, когда наблюдается реальный рост покупательной способности вложенного капитала

Также выделяют отрицательную процентную ставку, когда h > i, соответственно имеем снижение покупательной способности вложенного капитала (не говоря о доходности).

Для снижения воздействия инфляции и компенсации потерь от снижения покупательной способности денег применяют различные методы.

Наиболее распространенный – ИНДЕКСАЦИЯ ПРОЦЕНТНОЙ СТАВКИ

При этом осуществляется корректировка процентной ставки в соответствии с темпом инфляции.

Величина корректировки должна оговариваться в контракте.

Ставку, скорректированную на инфляцию условно наз. брутто-ставкой

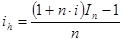
где 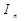- индекс инфляции

n – срок кредита

i – номинальная ставка процента

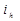- брутто-ставка

Другим способом учета инфляции является использование ф. Фишера:

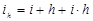
где 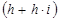- инфляционная премия

Инфляционная премия – это такая величина, которую необходимо прибавить к ставке доходности для компенсации инфляционных потерь.

Использование ф. Фишера позволяет избежать распространенной и, как правило, выгодной для кредитных учреждений ошибки, когда клиентам объясняется механизм компенсации их инфляционных потерь просто прибавлением h к i.

Дата добавления: 2013-12-12