
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Гюйгенса-Штейнера
|
|
|
|
Момент инерции тела. Теорема Гюйгенса-Штейнера. Примеры вычисления моментов инерции тел
Момент инерции тела аддитивная величина, равная сумме моментов инерции всех частиц тела:
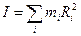 .
.
Здесь mi — масса i -той частицы, которую можно связать с плотностью вещества r i и объёмом частицы:
mi = r i D Vi.
Тогда 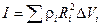 .
.
Если тело однородно, то есть его плотность повсюду одинакова, то r можно вынести за знак суммы:
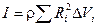 .
.
Разделяя тело на всё более мелкие частицы, сведём задачу отыскания момента инерции к вычислению интеграла:
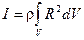 .
.
Интегрирование проводится по всему объёму тела V.
В качестве примера вычислим момент инерции тонкого однородного стержня относительно оси z, проходящей через его центр масс — точку С (рис. 9.3). Длина стержня — l, его масса — M.
На расстоянии x от оси вращения выделим элемент dx, масса которого dm = 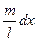 .
.
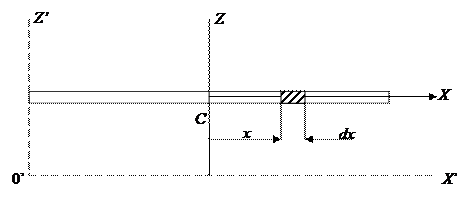
Рис. 9.3
Момент инерции этой частицы стержня равен:
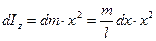 .
.
Вычислив подобным образом, моменты инерции всех элементов стержня, сложим их, взяв интеграл:
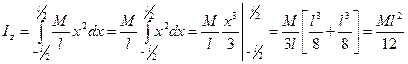 .
.
Таким образом:
Iz = 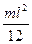 . (9.7)
. (9.7)
Интегрирование проведено по x в пределах от 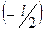 до
до 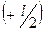 .
.
Как изменится момент инерции этого стержня, если ось вращения перенести в другое место? Провести её, например, через край стержня?
В этом случае прежний интеграл нужно рассмотреть в пределах от 0 до l:
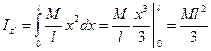 . (9.8)
. (9.8)
Новое значение момента инерции того же стержня заметно возросло. Связано это с тем, что момент инерции тела определяется не только его массой, но и её распределением относительно оси вращения.
Вычислим момент инерции ещё одного тела: сплошного цилиндра относительно его геометрической оси.
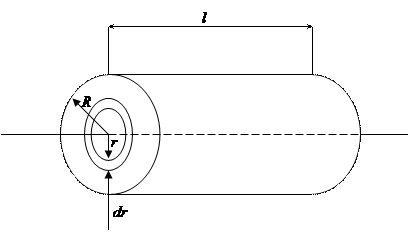
Рис. 9.4
Пусть M — масса, а R — радиус цилиндра (рис. 9.4). Выделим в этом цилиндре цилиндрический слой радиусом r и толщиной dr. Масса этого слоя:
dm = r × dV = r × 2p r × dr × l,
где: r — плотность материала цилиндра;
l — его длина.
Все частицы этого слоя находятся на одинаковом расстоянии от оси вращения — геометрической оси цилиндра, значит, момент инерции слоя равен:
dI = dm × r 2 = r × 2p r × dr × l × r 2.
Для отыскания момента инерции цилиндра проинтегрируем последнее выражение:
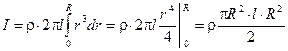 .
.
Отметим, что p R 2 l = V — объём цилиндра, а rp R 2 l = r V = M — его масса.
Тогда момент инерции цилиндра относительно его геометрической оси можно окончательно записать в таком виде:
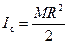 .
.
Момент инерции тела относительно произвольной оси (I) равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела М на квадрат расстояния между осями:
I = I c + Ma 2, (9.9)
где а — расстояние между осями.
На рисунке 9.5 оси вращения перпендикулярны плоскости чертежа: через точку 0 проходит произвольная ось; параллельная ей ось проведена через центр масс тела — точку С. Расстояние между осями — а.
Выделим элемент тела массой D mi. Его момент инерции относительно оси 0 равен:
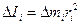 . (9.10)
. (9.10)
Как следует из рисунка 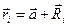 , откуда:
, откуда:
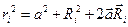 . (9.11)
. (9.11)
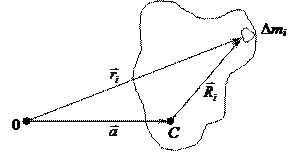
Рис. 9.5
Теперь момент инерции частицы D mi (9.10) можно представить такой суммой:
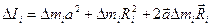 .
.
Для отыскания момента инерции всего тела, нужно сложить моменты инерции всех его частиц:
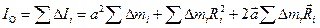 . (9.12)
. (9.12)
Здесь за знак суммы вынесена постоянная величина — расстояние между осями а. Первое слагаемое справа 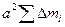 = Ма 2, так как
= Ма 2, так как 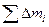 = М — масса тела. Второе слагаемое
= М — масса тела. Второе слагаемое 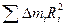 = I С — момент инерции тела, относительно оси, проходящей через центр масс. Третье слагаемое равно нулю, так как сумма
= I С — момент инерции тела, относительно оси, проходящей через центр масс. Третье слагаемое равно нулю, так как сумма 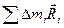 равна произведению массы тела на вектор
равна произведению массы тела на вектор 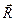 , проведённый от оси С к центру масс тела. Но ось С проходит через центр масс, поэтому
, проведённый от оси С к центру масс тела. Но ось С проходит через центр масс, поэтому 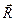 = 0 и
= 0 и 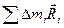 = М
= М 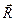 = 0.
= 0.
Собрав эти результаты в уравнение (9.12), получим выражение теоремы Гюйгенса-Штейнера:
I O = I C + Ma 2.
Эта теорема значительно упрощает задачу вычисления моментов инерции.
Известен, например, момент инерции стержня относительно оси, проходящей через его центр масс (9.7):
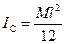 .
.
Воспользовавшись теоремой Гюйгенса-Штейнера, легко вычислим момент инерции этого же стержня относительно оси z ’, проходящей, например, через край стержня (рис. 9.3):
Iz ’ = Iz + Ma 2, a = l /2.
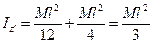 .
.
Это значение момента инерции совпадает с результатом (9.8), который был получен методом прямого интегрирования.
Лекция 10 «Механика твёрдого тела»
План лекции:
1. Полная система уравнений, описывающая произвольное движение твердого тела. Условия его равновесия и покоя.
2. Энергия движущегося тела.
2.1. Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси
2.2. Кинетическая энергия тела при плоском движении.
3. Скатывание тела с наклонной плоскости.
|
|
|
|
|
Дата добавления: 2013-12-11; Просмотров: 1224; Нарушение авторских прав?; Мы поможем в написании вашей работы!