Кинетическая энергия тела при плоском движении

Энергия движущегося тела

2.1. Кинетическая энергия твёрдого тела, вращающегося вокруг неподвижной оси

В твёрдом теле, вращающемся с угловой скоростью w относительно неподвижной оси z, выделим элемент массой D m_i. Эта частица будет двигаться по окружности радиуса r_i с линейной скоростью V_i = w r_i (рис. 10.3).

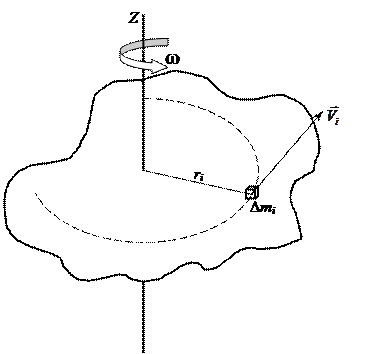
Рис. 10.3

Кинетическая энергия этой частицы равна:

.

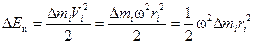Кинетическую энергию тела можно получить, сложив энергии всех его частиц:

.

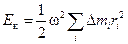Здесь 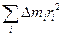= I_z — момент инерции тела относительно оси z, поэтому выражение кинетической энергии вращающегося тела окончательно представим так:

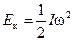. (10.6)

Этот результат напоминает формулу кинетической энергии поступательно движущегося тела:

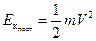. (10.7)

Различие только в том, что в одном случае при расчёте энергии используется масса тела и линейная скорость, в другом — момент инерции и угловая скорость вращения.

Любое движение твёрдого тела может быть представлено суперпозицией двух движений — поступательного и вращательного.

Представим плоское движение тела суммой поступательного со скоростью 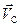, равной скорости центра масс, и вращения с угловой скоростью 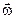вокруг оси, проведённой через центр масс тела — точку С.

Скорость i -той частицы тела (D m_i) будет равна векторной сумме её скоростей в этих двух движениях:

.

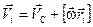Здесь 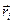— радиус-вектор частицы, определяющий её положение относительно точки центра масс — С (рис. 10.4).

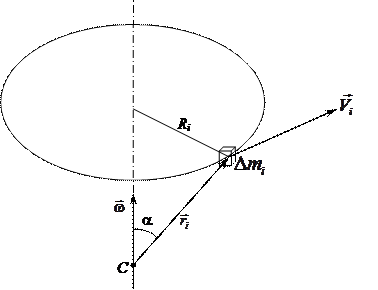
Рис. 10.4

Вычислим кинетическую энергию i -той частицы:

.

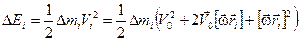Заметим (см. рис. 10.4), что модуль векторного произведения 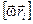равен:

,

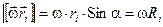где R_i — радиус круговой траектории частицы D m_i, или, что то же самое, — её расстояние от оси вращения.

Теперь раскроем скобки, попутно сделав циклическую перестановку сомножителей во втором слагаемом:

.

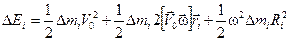Кинетическая энергия тела равна сумме энергий всех её частиц, поэтому:

.

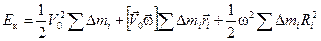Анализируя этот результат, приходим к следующим выводам:

Сумма 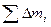= М равна массе тела.

Сумма 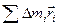равна произведению массы тела на радиус-вектор точки центра масс 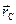. Но так как в этой задаче все радиус-векторы откладываются от точки центра масс, то 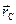= 0, и 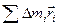= = 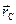0.

Сумма 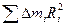= I _C представляет собой момент инерции тела относительно оси вращения, проходящей через центр масс (точку С).

Таким образом, кинетическая энергия тела равна:

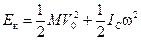. (10.8)

Представив движение суммой поступательного и вращательного движений, мы пришли к выводу, что кинетическая энергия плоского движения равна сумме энергий поступательного движения со скоростью, равной скорости центра масс V_С и вращения относительно оси, проходящей через центр масс тела:

.

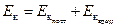Дата добавления: 2013-12-11