Закон эквивалентности массы и энергии

Основное уравнение релятивистской динамики

Экспериментально установлено, что в области релятивистских скоростей становится заметной зависимость массы частицы от скорости

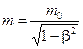, (14.3)

где: m — релятивистская масса;

m ₀ — масса покоя.

Основное уравнение динамики релятивистской частицы сохраняет форму второго закона Ньютона:

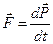. (14.4)

Однако здесь используется релятивистский импульс материальной точки:

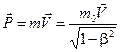. (14.5)

При невысоких скоростях (V << с) масса частицы становится равной массе покоя m = m ₀, а основное уравнение релятивистской динамики переходит в основное уравнение движения классической механики. Релятивистское уравнение движения (14.4) инвариантно по отношению к преобразованиям Лоренца (14.1).

В соответствии с законом Эйнштейна полная энергия системы пропорциональна её релятивистской массе:

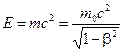. (14.6)

Связь энергии системы с её массой универсальна в том смысле, что справедливо и обратное утверждение: с любой энергией Е связана релятивистская масса m:

.

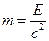В релятивистской механике полная энергия системы складывается из её кинетической энергии и энергии покоя:

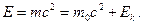(14.7)

Здесь: 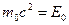— энергия покоя;

Е _к = (m – m ₀) c ² =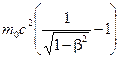— кинетическая энергия системы.

При скоростях V << c релятивистская кинетическая энергия переходит в классическую . .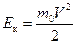

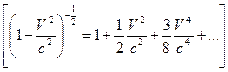В релятивистской механике неподвижное тело обладает энергией покоя E ₀ = m ₀ c ², которая не учитывается в классической механике.

Полная энергия замкнутой системы не меняется со временем. Этот закон сохранения энергии справедлив в релятивистской механике также как и в классической.

Решая совместно уравнения (14.5) и (14.6), найдем связь полной энергии системы с её импульсом:

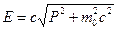. (14.8)

Отсюда можно получить ещё одну величину, инвариантную относительно преобразований Лоренца:

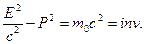(14.9)

Действительно, ведь масса покоя — m ₀ и скорость света — с — инвариантные величины. Инвариантность выражения (14.9) подтверждена экспериментально в опытах с быстрыми частицами.

Рекомендуемая литература:

1. Савельев И.В. Курс физики. Т.1. Механика.-СПб Мифрил. М.: Наука, 1996.

2. Стрелков С.П. Механика. М.: Наука, 1975.

3. Киттель Ч., Найт У., Рудерман М. Берклеевский курс физики, Т. 1. Механика.-М.: Наука, 1975.

4. Орир Дж. Физика. Т.1. –М.:Мир,1988

5. Трофимова Т.И. Курс физики. - М.:В.Ш.,1990.

Дата добавления: 2013-12-11