Дискретные случайные величины

Определение. Дискретная случайная величина — это такая величина, множество значений которой конечно или счетно. Обозначается x (кси), h (эта), ψ (пси), χ (хи).

Каждому k -у исходу случайного эксперимента поставим в соответствие единственное число x_k —значение случайной величины. Тогда естественно рассматривать случайную величину как функцию, определённую на множестве исходов случайного опыта. Функцию зададим таблицей. Например,

Таблица 1.

Исходы	Е1	Е2	Е3	Е4	Е5	Е6	Е7	Е8	Е9	Е10
xi	-2		-5	-2			-2	-2

или

Таблица 2.

xi	-5	-2
pi	0,1	0,4	0,3	0,2

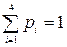
Обсудим, в чём отличие этих двух способов задания случайной величины?

--------------------------------------------------------------------------------------------------

Таким образом, задать случайную величину можно, просто представив её закон распределения.

Определение Закон распределения — это соответствие между значением случайной величины и вероятностью или последовательностью её появления. Закон распределения также может быть задан аналитически.

Задача 1. Стрелок стреляет в мишень два раза. Известно, что он попадает в мишень с первого выстрела с вероятностью 0,1. Если первый выстрел удачный, то при втором выстреле он попадает в мишень с вероятностью 0,7, если же первый выстрел неудачный, то при втором выстреле он попадает в мишень с вероятностью 0,5.

Написать закон распределения случайной величины ψ – числа попаданий в мишень.

Решение.

Очевидно,

ψ
pi

Найдем p_i.

Обозначим события 1 = { стрелок попал в мишень с первого выстрела }

2 = { стрелок попал в мишень со второго выстрела }.

P (1) = 0,1, P (2/1) = 0,7, P (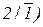) = 0,5. Тогда

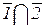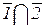x₁ = 0, {стрелок не попал в мишень} = и P 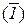() = P P 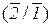= 0,9×0,5 = 0,45;

x₂ = 1, {стрелок попал в мишень один раз} = 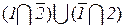и

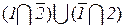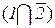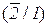P () = P + P = P (1) P 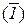+ P P = 0,1×0,3 +0,9 ×0,5 = 0,48;

x₃ = 2, {стрелок попал в мишень два раза} = 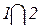и

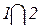P 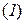() = P P 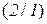= 0,1×0,7 = 0,07.

Получаем закон распределения

ψ
pi	0,45	0,48	0,07

Обращаем внимание, что .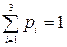

Дата добавления: 2013-12-13