Свойства неотрицательных матриц

Матрица полных затрат

Решение системы (2.3) определяется формулой 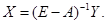Данная формула имеет важную экономическую интерпретацию. Разложим правую часть формулы в ряд

(2.7)

Для получения вектора X, обеспечивающего конечный спрос Y, необходимо сначала произвести количество продуктов Y. Для получения конечного продукта Y необходимо затратить количество продукции AY, которое нужно сначала произвести. Следовательно, ВВ включает в себя и вектор AY. При производстве вектора AY возникают дополнительные затраты , и т.д. Поэтому ряд (2.7) называется полными затратами на производство конечного спроса Y, а матрица (E – A)^-1 называется матрицей полных затрат.

Изложим эти свойства без доказательства. Всюду в данном разделе буквой А обозначается квадратная матрица с неотрицательными элементами, N— множество, состоящее из первых п натуральных чисел.

Определение. Пусть S ⊆ N, S' = N – S. Говорят, что множество S изолировано, если a_ij=0, как только i ∈S', j ∈ S. Понятие изолированности множества S допускает экономическую интерпретацию на языке модели Леонтьева. Так, изолированность множества S в модели Леонтьева означает, что отрасли, номера которых принадлежат множеству S, не нуждаются в товарах, производимых отраслями, номера которых принадлежат множеству S'. Если перенумеровать индексы так, чтобы S = {1, 2,..., k}, S'= {k + 1,..., n}, что соответствует одновременной перестановке строк и столбцов матрицы A, то матрица А примет вид

(2.8)

где A₁ и A₃ —квадратные подматрицы размеров k × k и (n – k)×(n – k) соответственно.

Матрица А называется неразложимой, если в множестве N нет изолированных подмножеств, т.е. если одновременной перестановкой строк и столбцов ее нельзя привести к виду (2.8). Неразложимость матрицы А в модели Леонтьева означает, что каждая отрасль использует хотя бы косвенно продукцию всех отраслей.

Отметим несколько простых свойств неразложимых матриц.

а) Неразложимая матрица не имеет нулевых строк и столбцов.

б) Если матрица A неразложима и y > 0, то Ay^T > 0.

в) Пусть y ≥ 0, y ≠ 0; тогда вектор z = (E + A)y^T имеет меньше нулевых координат, чем вектор у, если это возможно. Кроме того, если А неразложима x ≥ 0, x ≠ 0, то из неравенства Ax^T ≤ α x следует, что

α >0, x > 0.

г) Теорема 1. (Фробениус – Перрон о спектральных свойствах неотрицательных матриц).

1. Неразложимая матрица А имеет положительное собственное число λ А такое, что модули всех остальных собственных чисел матрицы А не превосходят λ _A.

2. Числу λ _A отвечает единственный (с точностью до скалярного множителя} собственный вектор Х_A, все координаты которого ненулевые и одного знака (т. е. его можно выбрать положительным). Собственные векторы Х_A и p_A матриц A и A^T соответственно, а также число C будем называть фробениусовыми.

Отметим, что если матрица А неразложима, то λ_A является единственным собственным числом, для которого существует неотрицательный собственный вектор. Неразложимую матрицу А будем называть устойчивой, если для любого вектора х последовательность A^kx,k=1,2,…, сходится. Пример матрицы, не являющейся устойчивой:

Неразложимая матрица А называется циклической, если множество N = {1, 2,......, n} можно так разбить на m непересекающихся подмножеств , что если a_ij > 0, i ∈ Sr, r ≥ 1, то j ∈ Sr-1, а при i ∈ S₀ j ∈ Sm-i. Остальные неразложимые матрицы называются примитивными.

Теорема 2. Примитивная матрица устойчива. Эта теорема устанавливает зависимость свойства матрицы быть устойчивой от ее внешнего вида. Вместе с тем свойство матрицы быть устойчивой полностью определяется и свойствами ее спектра – множеством собственных чисел. Справедливо следующее утверждение.

Неразложимая неотрицательная матрица А устойчива тогда и только тогда, когда выполняется неравенство | λ |< λ_A для любого ее собственного числа λ ≠ λ А.

Дата добавления: 2013-12-13